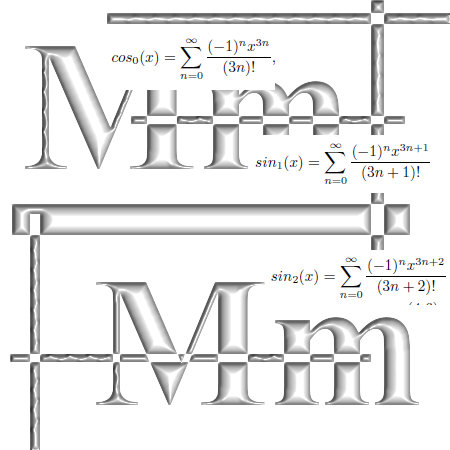
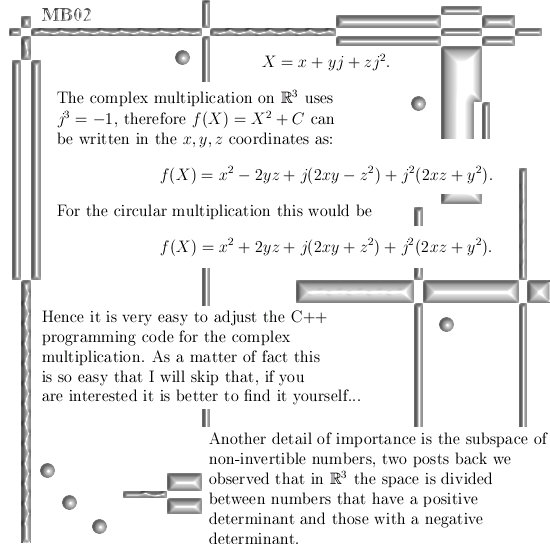
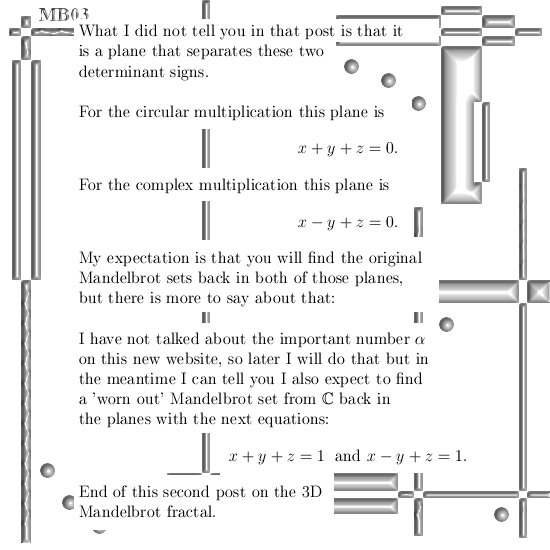
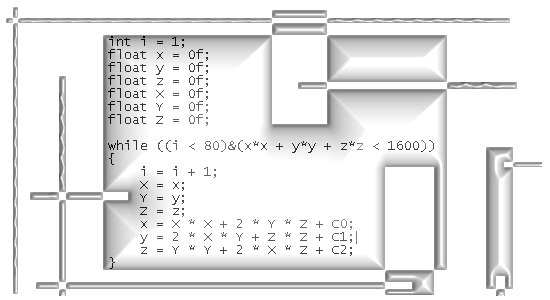
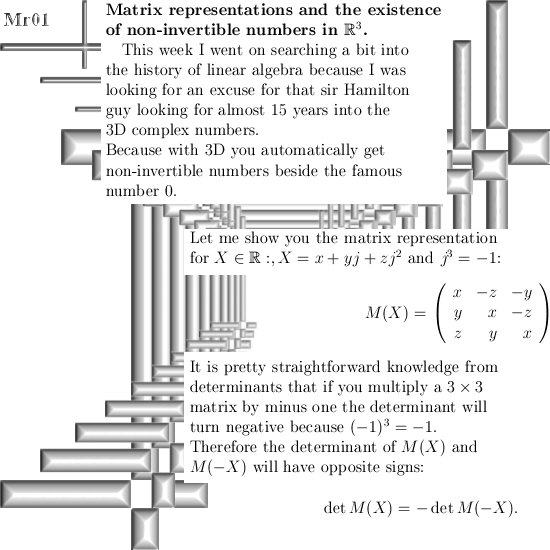
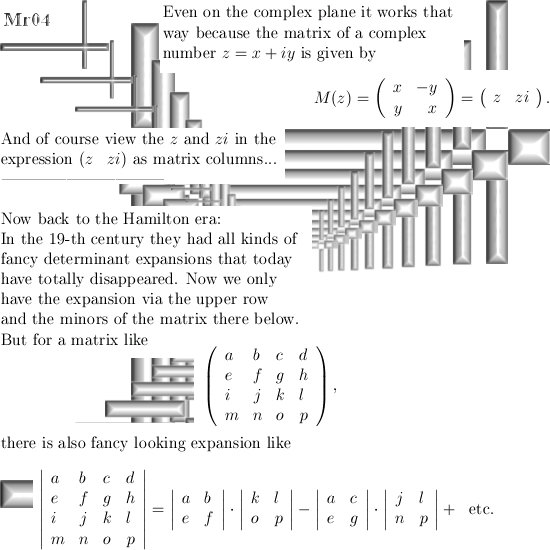
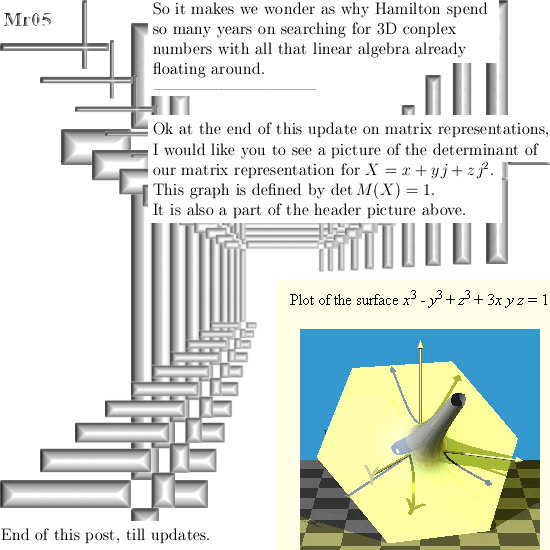
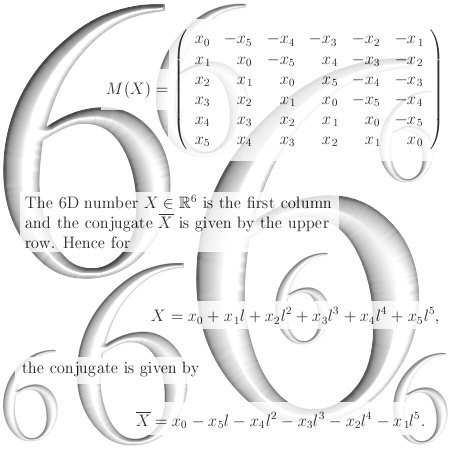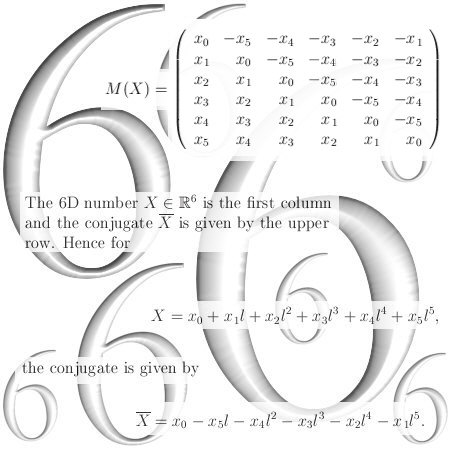Monthly Archives: January 2016

Calculating the Laplacian using the Cauchy-Riemann equations.

January 30, 20163D complex numbers, CR equations, LaplacianReinkoVenema

Without doubt the Laplacian is a very important differential operator. It plays a major role in for example the classical wave equation and also the Schrödinger wave equation from quantum mechanics.

Now scroll a bit back until you find the post on the Cauchy-Riemann equations, at the end I used the phrase ‘Cauchy-Riemann equations chain rule style’ and this is how we can crack in a very easy way how the Laplacian operates on functions that obey the CR equations on 3D complex numbers.

I have hundreds and hundreds of pages of math stuff on the 3D complex number system and very often I use the number alpha. This number alpha is so important, not only in 3D, that it is worth to post a few posts on them.

For the time being, I just conducted a simple Google search on the phrase ‘3d complex numbers’ in the search detail for pictures. And every time this old teaser picture from the other website pops up:

At the end you see that (1, -1, 1), well that is three times alpha.

It is a nice exercise to prove that the square of alpha equals alpha.
So alpha is in the same category as for example numbers like 0 and 1 because if you square those you also get the original number back in return.

After all one squared equals one and zero squared equals zero.

End of this update, till updates.

Math muscle, does it exist?

January 21, 20163D complex numbersReinkoVenema

Two days ago I found that article from a Israeli citizen on the preprint archive. It is well known that the Jewish part of the Israeli society have a very high Nobel prize to capita citizen ratio.

Very likely they have the most Nobel prizes per capita citizen of our small planet…
There are a lot of reasons for this, for example Israelis think about the food they eat. (I mean try to eat some of that weird McDonnalds food and make a math exam later, good luck with it.)

But this post is not about why the Jewish society has so many Nobel prizes, it is about showing off my math muscles. Math muscles? Do they exist?

To my amazement the guy Shlomo Jacobi even investigated the alternating sums as shown below.
He understood the importance of the stuff involved, but was likely not capable of finding the explicit formulaes…

___________

So now we are comparing math muscle:
The next picture is what the Jacobi guy brings up:

Please remark this is just a power series any math student can write down, what is the solution?
And from an update known as the Curves of Grace, I found the explicit stuff.
I recycled this picture from Google search pictures because that saved me a bit of time:

Remark you must replace the x by the time variable t in the Taylor series…
It is a typo because in the past I wrote them with x while now I needed them it had to be in time t.

So ok ok, since I want this to be a nice new website it took about 10 minutes to find a corrected version of this. In the meantime I observed how much work I have done over the last 8 months.
Here is the corrected version:

__________

So between me and the Israeli math departments from the universities they have over there, this is just a bit of showing off my math muscles…

Source links: preprint archive of the Jacobi guy: http://arxiv.org/abs/1509.01459
My work on the curves of grace: http://kinkytshirts.nl/rootdirectory/just_some_math/3d_complex_stuff03.htm#18April2015

Till updates my dear reader.

And now we are with three…

January 19, 20163D complex numbers, CR equations, Exponential circleReinkoVenema

In Oct 1990 (estimated) I found the 3D complex numbers, a few years back I discovered that a guy named Dennis Morris has found them too. Dennis even wrote a book about it, this book was published twice and I was able to get a hand on the second publication.

For normal humans the book from Dennis is a good starter, for me it has the depth of a bird bath.

We do not complain, today on the preprint archive I found the next pdf file:

On a novel 3D hypercomplex number system
http://arxiv.org/pdf/1509.01459v1.pdf

And this work has not the depth of a bird bath, it is much more the depth of a human bathtub.
There ar some dumb typo’s, for example table 1 contains a very stupid error so that has to be corrected.

The writer of the preprint article goes under the name of Shlomo Jacobi and since his residence was Israel we might jump to the conclusion he was a Jew. Let religion be no problem because after all the Muslims were once far ahead of the Western powers but because one of their religious leaders declared math as being from the devil, Muslims find themselves at the receiving end of military powers for about one thousand years…

Now back to our Jewish pdf file: Table 1 should be corrected and I, Reinko Venema, I give them a big applause because if you scroll down to page 39 you observe they have found the 3D exponential circle too!

Well I have found all exponential curves in all possible dimensions, so I am very pleased to invite the Jewish mathematical community upon further investigations into this math detail.

End of this update, till updates.

Correction on the 08 Dec 2015 post; there are two typo’s…

January 17, 20163D complex numbers, Corrections, Matrix representationReinkoVenema

It is not a big deal because every person who understands a bit about how matrix representations work sees instantly these must be two typo’s.

But recently about once a week I am scanning how this new website is doing in search engines like Google. And I am very satisfied, every post can now pop up as a separate search result and for example on pictures to my surprise the next picture popped up as pic number six if you search for ‘3d complex numbers’.
This is the version with the two typo’s in it:

And here is the corrected version:

So it is not a big deal but if a search result ends that high it is not unwise to correct it.
And to be honest, I know for years that you can craft let’s say 15 dimensional complex numbers from 3D and 5D complex numbers.
But to be honest, I had never done it until the December update from last year.

And I have learned some stuff too, only if you dive into those technical details like how those basis vectors are actually related you appreciate it so much more.
You know the nicest thing about higher dimensional complex numbers is very simple: I know for sure I am about one of the first humans to hang around in those spaces.
Beside the mathematical beauty the stuff has, it has also that old stuff like discovering new lands that is basically baked into the human genome.

Ok, enough of the phylosofical bla bla. Till updates.

The 3D Mandelbrot set. Part two.

January 14, 2016UncategorizedReinkoVenema

With my previous post I thought that I am leaving behind a lot of readers into the woods. But the goal of this new website is making easy to digest updates.

Therefore just three pictures explaining a bit more about the 3D Mandelbrot set.
I wish the computer code writing folks a lot of luck; if you are the first that
has a view on the 3D Mandelbrot set you have won the race.

By the way; out there is something known as the Mandelbulb or so. It looks nice but believe it has nothing to do with the 3D Mandelbrot set. This Mandelbulb thing is not based upon a reliable way of multiplication in three dimensions, the results they found are nice looking but it is just not based on a rigid way of 3D multiplication…

Anyway, here are three pictures all sized 550 by 550 pixels that should shine a bit more light on the minds of those that write the code:

$0008=14Jan2016=3D_Mandelbrot_fractal01$

$0008=14Jan2016=3D_Mandelbrot_fractal02$

$0008=14Jan2016=3D_Mandelbrot_fractal03$

On a video channel named Numberphile from Google they have a good explanation about how to color the pixels according to the Mandelbrot scheme. Here is the link:
The Mandelbrot Set – Numberphile

In all dimensions where complex numbers can be defined, you can do this…
Till updates, think well and live well.

Short stuff on the 3D Mandelbrot fractal.

January 13, 20163D complex numbersReinkoVenema

About a year ago I decided to take about two years to make it to the 3D Mandelbrot set. So I tried to learn one of those modern programming languages like C++, I did build a new computer because on my old system C++ would not run. And so on and so on.

Decades ago I tried to learn a computer programing language known as Basic. When I found out how those kind of programming languages evaluted an integral, I almost had to vomit.
In those long lost years I already developed a fundamental dislike against programming.

Now I am 52 years of age and it is still the same; me writing computer code is not a happy thing to do. So I killed the project of being the first person on this planet to view the 3D Mandelbrot set using the 3D complex or circular multiplication…

I never made it beyond what is in C++ a ConsoleApllication; you get your output in an old fashioned DOS screen and no graphics at all. And how to embed this into a thing you can actually fly through, I have given up on that.

So I did not write much code, but the results had all you expected it should have: Strong sensitivity to initial conditions and so on and so on.

Well here is the kernel of the 3D Mandelbrot set for the circular multiplication.
Circular simply means we are using 3D circular numbers X = x + yj + zj^2 where j^3 = 1.

In this kernel we have to use so called ‘dummy variables’ because computers are so stupid you cannot tell them how to calculate the next round of variables This despite in the year 2016 most desktops have multiple cores, your programming language still uses the old von Neuman principles.

Here is the kernel with the dummy variables written as capital X, Y and Z while we only want to know how the x, y and z evolve over the iterations… :

int i = 1;
float x = 0f;
float y = 0f;
float z = 0f;
float X = 0f;
float Y = 0f;
float Z = 0f;

while ((i < 80)&(x*x + y*y + z*z < 1600))
{
i = i + 1;
X = x;
Y = y;
Z = z;
x = X * X + 2 * Y * Z + C0;
y = 2 * X * Y + Z * Z + C1;
z = Y * Y + 2 * X * Z + C2;
}

__________

Oh oh my dear Mandelbrot baby, now I have thrown you into the river I will never be the first human to observe your intrinsic details. Let it be, let it be because for the rest of my life I can still hate that stupid computer code writing.

Till updates.

Some people will do everything wrong…

January 3, 20163D complex numbersReinkoVenema

This is a very short update from a guy that likely goes under the name of Alen.
Now for years Alan has a very weird page hanging out there and he tries to describe the 3D complex numbers as they should be in his view…

Very very likely this is the approach Hmilton took for 12 to 15 years; it leads to all kinds of horrible difficulties, technical disasters and an end result useless to all people on the globe.

Now you must not jump to the conclusion that I hold this Alen person for some idiot. It is rumored that at any given time there are about 100 thousand professinal math workers out there and I do not mean high school teacher but people from the universities and stuff like that.

All these people cannot find higher dimensional complex number systems themselves either…
Ok, enough of the bla bla bla en prepare yourself to dive in the blurry and fuzzy mindset of how people thought 3D complex numbers must be (it is always with something squared that is minus one…):

N-DIMENSIONAL COMPLEX NUMBERS.
http://www.alenspage.net/ComplexNumbers.htm

Matrix representations and how to craft them.

January 1, 20163D complex numbers, Matrix representationReinkoVenema

Here it is still 01 jan 2016 so a happy new year.
In this update with five pictures with the standard size of 550 by 550 pixels we are going to look at how to craft matrix representations for higher dimensional complex numbers.

It is all rather basic stuff.

Here we go with post number 1 in the year 2016: