Monthly Archives: May 2024

Eigenvalue functions for the elliptic complex plane.

2D multiplications

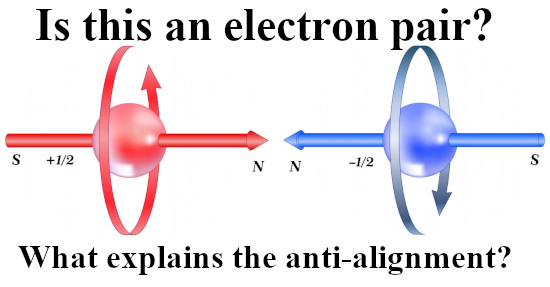
This is a very short post, in it I even joke this is done in “Tik Tok style”. It is about finding the eigenvalues for an arbitray elliptic complex number. Such numbers have matrix representations and as such they have also eigenvalues that live in the ordinary complex plane.
Here the elliptic plane is the same as we always studied the last couple of months, it is ruled by the imaginary unit i via i^2 = -1 + i. If you need the eigenvalues of such a number, instead of going through the calculation for eigenvalues every time, with the eigenvalue functions you just substitute it in and it spits out the two eigenvalues.
To be honest I did not explain in detail why it works, I hope it is rather obvious. Take for example two commuting (square) matrices A and B. They have the same eigen vectors (because they commute) and as such it is very easy to find the eigenvalues of any linear combination of A and B.

The post itself is only two pictures long and I included a third picture that I used on the other website. Beside a female robot the third picture contains another factorization of the equation of the ellipse that is the determinant of the matrix representations.
So this equation for the ellipse can be factored on the standard complex plane and also on the elliptic complex plane. The interesting detail is of course that on the elliptic complex plane you have integer coefficients while on the standard complex plane this is impossible.

Basically the eigenvalue funtions are both a map from the elliptic complex plane to the ordinary complex plane. If it was made by a professional math professor he or she would likely call it an isomorphism but I name them eigenvalue functions. In the past I also made them for the 3D complex and circular numbers and of course for the 4D complex numbers that were under study years ago.
Enough of the introdutionary talk, lets go:

There is a small ‘cut & paste’ error at the top of the next picture.

Now I left a lot of stuff out otherwise it would not be a Tik Tok short kind of math post. But you can also use the elliptic complex plane as your primary source of eigenvalues. For example at the other side of our galaxy there lives an alien race known as the Orcs. And for some kind of religious reason these Orcs just don’t want to use circles because as they all know circles are evil. But they found the elliptic complex plane and they use that for solving eigenvalue problems like eigenvalues from square matrices or even stuff that we humans know as the Hamiltonian energy operator. That should work just as good as we humans do in using the complex plane we have over here where the complex exponential is a circle.
So let us now look at the third picture that has both factorizations in it:

This cleary is not for math professors; they won’t understand this conjugate.

Let me leave it with that and as always thanks for your attention.

The cousin of the transponent.

2D multiplications, 3D complex numbers, Matrix representation

Likely in the year 1991 I had figured out that the conjugate of a 3D complex number could be found in the upper row of it’s matrix representation. As such the matrix representation of a conjugate 3D number was just the transpose of the original matrix representation. Just like we have for ordinary complex numbers from the complex plane. And this transpose detail also showed that if you take the conjugate twice you end where you started from. Math people would say if you do it twice, that is the identity operation.
But for the two 2D multiplications we have been looking at in the last couple of months, the method of taking the upper row as a conjugate did not work. I had to do a bit of rethinking and it was not that hard to find a better way of defining the conjugate that worked on all spaces under study since the year 1991. And that method is replace all imaginary units by their inverse.
As such we found the conjugate on 2D spaces like the elliptical and hyperbolic complex planes. And the product of a 2D complex number z with it’s conjugate nicely gives the determinant of the matrix representation. And if you look where this determinant equals one, that nicely gives the complex exponentials on these two spaces: an ellipse and a hyperbole.
Now when I was writing the last math post (that is two posts back because the previous post was about magnetism) I wondered what the matrix representation of the conjugate was on these two complex planes. It could not be the transpose because the conjugates were not the upper rows. And I was curious what it was, it it’s not the transpose what is it? It had to be something that if you do it twice, you do the identity operation…

All in all in this post the math is not very deep or complicated but you must know how te make the conjugate on say the elliptic complex plane. On this plane the imaginary unit i rules the multiplication by i ^2 = -1 + i. So you must be able to find the inverse of the imaginary unit i in order to craft the conjugate. On top of that you must be able to make a matrix representation of this particular conjugate. If you think you can do that or if you don’t do it yourself you will understand how it all works, this post will be an easy read for you.

It turns out that the matrices of the conjugate are not the transpose where you flip all entries of the matrix into the main diagonal. No, these matrix representation have all their entries mirrored in the center of the matrix or equivalently they have all their entries rotated by 180 degrees. That is the main result of this post.

So that’s why I named it the “Cousin of the transponent” although I have to admit that this is a lousy name just like the physics people have with naming the magnetic properties of the electron as “spin”. That’s just a stupid thing to do and that’s why we still don’t have quantum computers.

Enough intro talk done, the post is five pictures long and each picture is 550×1200 pixels. Have fun reading it.


That was it for this post, one more picture is left to see and that is how I showed it on the other website. Here it is:

Ok, this is really the end of this post. Thanks for your attention and may be see you in another post of this website upon complex numbers.

On a video about spin ice & some additional remarks.

Magnetism

A couple of weeks back I already showed this video from Dr. Erica Carlson on the other website. I did select that video because in the second half of that video she talks about electron spin configurations that minimize the energy in stuff that is known as spin ice.
Since all those energy problems that I have with viewing electrons as bipolar tiny magnets are always skipped, I decided to use this video as a short post on magnetism. In videos like this the pattern is always the same: at the surface it all looks logical like in this video the spin configuration in that stuff known as spin ice. But video after video I have seen over the last years, always when we need to look at crazyland they always skip that. When the energy stuff gets crazy, they just skip it. Now this is absolutely not some form of a conspiracy, these people like Erica simply believe the bipolar magnetic electron is true and as such they have a blind spot into the problems: They just don’t see the problems because of their blind spot.

In the year 2015 I started to doubt that electrons were tiny magnets with two magnetic poles. I started doubting that after I tried for myself to explain the results of the so called Stern-Gerlach experiment. In my view the results were only explainable if we use magnetic monopole electrons. A few days later reading all those official explanations I understood I had to be cautious. And at the begining back in 2015 I knew nothing about electron spin, all I knew was that people from physics thought they were tiny (bipolar) magnets. It’s been a long journey from there back in 2015 and it will also be a long long journey going from our present year 2024. After all the belief that electrons are tiny macroscopic magnets is deeply rooted in 100% of the physics community.

In this post, for the first time since 2015, I included a simple expression about how the professional physics professors view the potential energy of electrons related to magnetism. It is somewhere below and it is the same as we have for macroscopic magnets like say two bar magnets.
If you hold two bar magnets south to north pole, that is the minimum potential energy because it costs energy to separate them. And if you hold two bar magnets say north pole to north pole, that is the situation of high potential energy.

The post itself is four pictures and two additional figures and of course the perfect video from Dr. Erica Carlson. Say for yourself, this video is a perfect 10 with all kinds of animations I can only dream of. Ok ok, there is just one tiny tiny error in it: electrons are not tiny magnets.
But for the rest it’s a “PERFECT 10” kind of video.

Well bipolar physics freaks: what is your explanation in detail?

That was more or less the end of this post but I made one more picture depicting another big energy problem that the official version of electron spin has: The behavior of a single electron in an applied magnetic field.

After all if it were true that electrons are tiny magnets, if you apply a magnetic field to electrons shouldn’t they all perfectly align with that magnetic field and as such fall into their lowest potential energy state?

Yes in an ideal world they should, but we live in a world where we not only have a lot of professional physics professors but also television physics professors. And they never talk about the energy problems there are with the electron as being tiny magnets.
So this is a strange strange world where physics just ingores simple problems like the last picture of this post:

Oh yes the stability problems we have if it were true that electrons are tiny magnets. As you see in the video it is always skipped and their brains never go down that route… It is what it is and here is the video:

Erica knows how to flip a spin…

Lets leave it with that, the next post will be about matrix representations of conjugtes of 2D complex numbers. They are weird and also lovely now I have my new method of understanding the process of conjugation.
And as always thanks for your attention and not falling asleep before you read these last words of this post.

Another way of finding the direction of the number tau.

2D multiplications, 3D complex numbers, 4D complex numbers, Matrix representation

A bit like in the spirit of Sophus Lie lately I was thinking “Is there another way of finding those tangets at the number 1?”. To focus the mind, if you have an exponential circle or higher dimensional curve, the tangent at 1 is into the direction of the logarithm you want to find.
In the case of 2D and 3D numbers I always want to know the logarithm of imaginary units. A bit more advanced as what all started a long time ago: e^it = cos t + i sin t.
An important feature of those numbers tau that are the sought logs is that taking the conjugate always the negative returns. Just like the in the complex plane the conjugate of i is –i.

The idea is easy to understand: The proces of taking a conjugate of some number is also a linear transformation. These transformations have very simple matrices and there all you do is try to find the eigenvector that comes with eigenvalue -1.
The idea basically is that tau must like in the direction of that eigenvector.

That is what we are going to do in this post, I will give six examples of the matrices that represent the conjugation of a number. And we’ll look at the eigenvectors associated with eigenvalue -1.

At the end I give two examples for 4D numbers and on the one hand you see it is getten a bit more difficult over there. You can get multiple eigenvectors each having the eigenvalue -1. Here this is the case with the complex 4D numbers while their ‘split complex’ version or the circular 4D numbers have not.
Now all in all there are six examples in this post and each is a number set on it’s own. So you must understand them a little bit.
The 2D numbers we look at will be the standard complex plane we all know and love, the elliptic and hyperbolic variants from lately. After that the two main systems for 3D numbers, the complex and circular versions. At last the two 4D multiplications and how to take the conjugate on those spaces.

The post itself is seven pictures long and there are two additional pictures that proudly carry the names “Figure 1” and “Figure 2”. What more do you want? Ok, lets hang in the pictures:

The purple line segment points into the direction of tau.
That’s why 4D split complex numbers are just as boring as their 2D counter parts.

Years ago it dawned on me that the numbers tau in higher dimensional spaces always come in linear combinations of pairs of imaginary units. That clearly emerged from all those calculations I made as say the 7D circular numbers. At the time I never had a simple thing to explain why it always had to be this pair stuff.
So that is one of the reasons to post this simple eigen vector problem: Now I have a very simple so called eigen value problem and if the dimensions grow the solution always come in pairs…

That was it for this post, likely the next post is upon so called ‘frustrated’ magnetism because the lady in the video explains the importance of understand energy when it comes to magnetism. After that may be a new math post on matrix representations of the actual conjugates, so that’s very different from this post that is about the matrices from the process of taking a conjugate…
As always thanks for your attention.