Monthly Archives: June 2016

Modified Dirichlet kernels for low dimensions.

3D complex numbers, 5D complex numbers, Exponential circle, Exponential curves

What the hydrogen bomb is in the average nuclear arsenal, that is what modified Dirichlet kernels are for higher dimensional complex & circular number systems.
Via the so called tau calculus I was able to achieve results in 3 and 5 dimensional number systems and I really had no hope in making more progress in that way because it gets so extremely hardcore that all hope was lost.

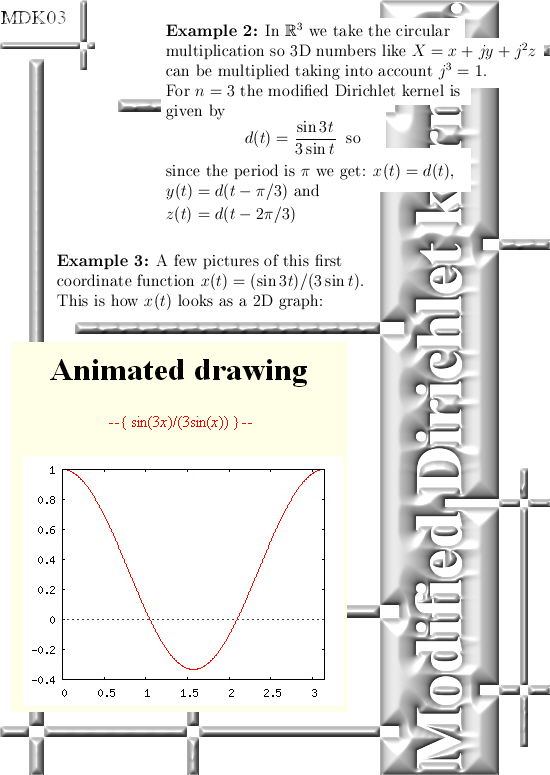
Yet about two years ago I discovered a very neat, clean and very beautiful formula that is strongly related to the Dirichlet kernel known from Fourier analysis. The formula I found was a dressed down version of the original Dirichlet kernel therefore I named it ‘modified Dirichlet kernel’.

This modified kernel is your basic coordinate function, depending on the dimension of the space you are working in you make some time lags and voila: There is your parametrization of your higher dimensional exponential (periodic) curve (only in 2D and 3D space it is a circle).

For myself speaking: this result of finding the modified Dirichlet kernel is for sure in my own top 10 list of most important results found. Not often do I mention other mathematicians, but I would like to mention the name of Floris Takens and without knowing how Floris thought about taking a sample of a time series and after that craft time lags on that, rather likely I would not have found this suburb and very beautiful math…

__________

I haven’t decided what the next post will be about.
It could be stuff like:

  • How I found the first modified Dirichlet kernel, or
  • Wirtinger derivatives for 3D number systems, or
  • Wow man, can you factorize the Laplacian operator form Quantum Mechanics???

But factoring the Laplacian requires understanding 3D Wirtinger derivatives so likely I will show you how I found the very first modified Dirichlet kernel.

__________

This update contains six jpg pictures each about 550 x 775 pixels and two old fashioned animated gif pictures. I tried to keep the math as simple as possible and by doing that I learned some nice lessons myself… Here we go:

0026_20June2016_Modified_Dirichlet_kernels01

 

This is the animated gif using z = 0 in 3D while this picture is showing the Euler exponential circle:

17-06-2016_exp_circle_on_C0026_20June2016_Modified_Dirichlet_kernels02

 

0026_20June2016_Modified_Dirichlet_kernels03

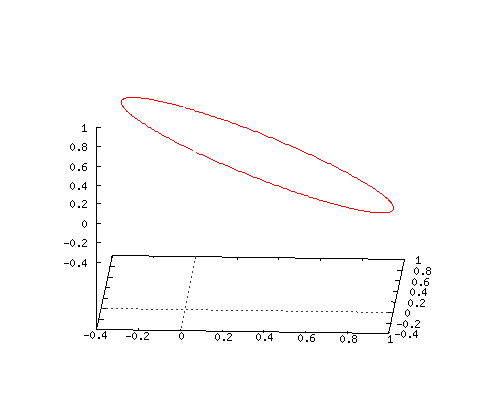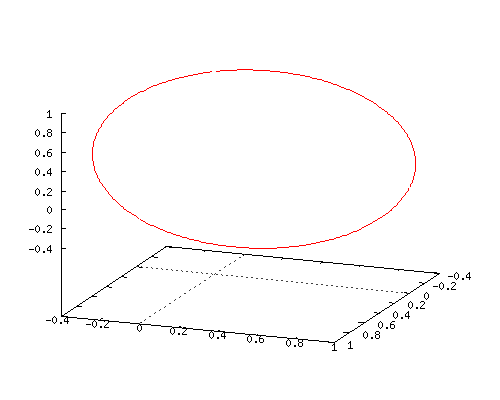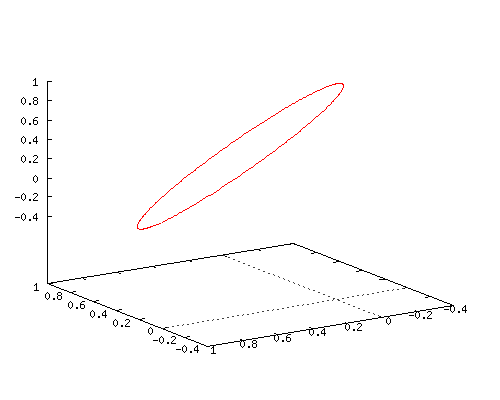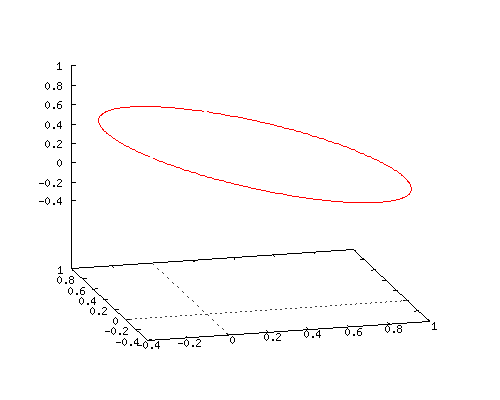
Here is an animated gif of how this coordinate function looks when you combine it with the two time lags for the y(t) and z(t) coordinates. Does it surprise you that you get a flat circle?
If it does not surprise you, you do not understand how much math is missing in our human world…

17-06-2016_exp_circle_on_3D_circular

0026_20June2016_Modified_Dirichlet_kernels04

0026_20June2016_Modified_Dirichlet_kernels05

0026_20June2016_Modified_Dirichlet_kernels06

In case you are interested in the ‘time lag’ idea as Floris used it, here is a nice Youtube video that gives a perfect explanation. If you apply this time lag idea for example is a 17 dimensional real vector space you get a 17D exponential curve with all of it’s magnificent properties…

Takens’ theorem in action for the Lorenz chaotic attractor

Yes, end of this post. See ya around & have a nice life or try to get one.

More proof for electrons being magnetic monopoles.

Magnetism, Uncategorized

This post is another advertisement for the magnetic page on the other website with the funny name:

A primer on the electrons that are the long sought magnetic monopoles. Author: Reinko Venema.
http://kinkytshirts.nl/rootdirectory/just_some_math/monopole_magnetic_stuff.htm

Ok, in the previous post I said the next one would be on the modified Dirichlet kernels but I did not update the magnetic page for over one month so I had to rearrange priorities.

When riding my noble iron horse through the local landscape I was thinking about how professional physics professors would waive away my insights with just a little hand waive while mumbling ‘Lorentz force’.
Just like they do when explaining the electron spin, they say stuff like: It is spinning and when an electrical charge is spinning it creates a magnetic dipole moment (in the meantime they also shrug their shoulders a little bit and move on with the lesson).

Now while riding my noble iron horse (a 269 € bicycle) I suddenly thought:
What would happen if I cut my stack of strong neodymium magnets into two pieces and use that???

And hurray: It was a big success; there was some strong asymmetry observed and I think this might be a manifestation of the Lorentz force. This is not rock solid proof because I do not know how strong the magnets are and as such I have no clue about the radius induced by the Lorentz force.
But this looks very promising.

Here is the first photo, on the black spot no electrons slam into the television screen:

0025_12June2016_new_photos01

Under the assumption electrons are magnetic monopoles and as such carry a magnetic charge just like they carry an electric charge, the next is observed/happening:

  1. The color television has three electron cannons, each electron is attracted or repelled by the strong neodymium magnets.
  2. As such the electrons slamming into the screen in between the two stacks of strong magnets are the attracted ones while those that are repelled are found on the outside of the black region.
  3. In the dark region no electrons land on the screen, a feature that cannot be explained by any of the Maxwell equations or the Lorentz force.

In the next photo you see that I am trying to make the region of attraction horizontal, but for that to happen I have to place the magnet stacks more or less diagonal:

0025_12June2016_new_photos02The costs of this experiment are below 50 €, the television was only 6 € and the magnets about 40 € included shipping and handling. This is a very important detail because over at CERN they always burn an extreme amount of money before they get any kind of result.

It is also important because high schools in my country often have lousy budget for physics experiments so for 50 € you have a perfect thing to show to the pupils/students…

All in all this is reason number 30 as why electrons carry magnetic charge (aka they are the long sought magnetic monopoles):

12 June 2016: Reason 30: New photo’s from a television experiment
http://kinkytshirts.nl/rootdirectory/just_some_math/monopole_magnetic_stuff.htm#12June2016

Ok, thanks for your attention and till updates!

Three centuries after de Moivre finally some new baby steps.

3D complex numbers, Exponential circle

I am a little bit late with this post but after the previous post I took some time to enjoy it because not every day you can craft a brand new coordinate system…

Also I was a bit in doubt about this post, shall I finally start with those modified Ditichlet kernels or work out a simple de Moivre example in 3D? It became the latter so likely in the next post I will do some first things with modified Dirichlet kernels.

This post is just 4 pictures long (size 550 x 775 pixels) and to be honest it contains no serious math whatsoever. I was only driven by curiosity about how difficult a simple example of the new 3D versions of it would be.
Now it is not 100% trivial but it is also not a very deep result, at best you can say it is a bit technical because you constantly have to apply those sum and difference formulae for the cos and sine functions.

The real deep math work was crafting those exponential circles in 3D in the first place and later finding the coordinate functions belonging to that. That was the deep math because once you have those, the new de Moivre formulae are a piece of cake (make sure it is gluten free!).

__________
In this update I also would like to make an advertisement for a long update I started about one year ago on the other website; all in all it is 37 pictures long (size 550 x 1100) and it took about 3 weeks to write it. It has the title The Missing Equations because with those modified Dirichlet kernel I knew I had solved a terrible hard problem but the higher in the dimensions I got the more missing equations I had for my wonderful solution… Here is the link:

From 14 July 2015: The missing equations.
http://kinkytshirts.nl/rootdirectory/just_some_math/3d_complex_stuff03.htm#14July2015

__________

After this small advertisement here are the four pictures of this update:

0025_05June2016_de_Moivre_baby_steps01

0025_05June2016_de_Moivre_baby_steps02

0025_05June2016_de_Moivre_baby_steps03

0025_05June2016_de_Moivre_baby_steps04

Once more: This is not a deep mathematical result or so.
I was just curious of how difficult it would be to get one of the most simple 3D new de Moivre formula results using only the 3 century old stuff from about 50 years before Euler entered the scene…

The most important lesson you can learn from this is that instead of focusing on all kinds of details like n = 2 and only the real part and so on is a waste of time and energy.
After all using the exponential circle is what brings peace to the heart; it is simple, it covers all powers at the same time and you have all coordinate functions at once…

__________

Now you have to wait a few minutes more because I would like to pop up a fresh home brew and after that I will hit the ‘publish post’ button…

Thanks for the waiting 😉 Now I will hit the publish button and see you next time around!