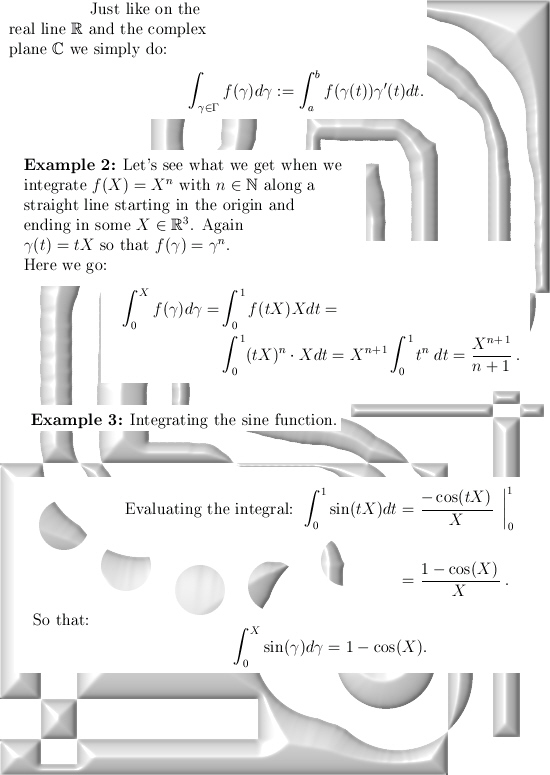
Ok, the math text is finally written. It took a long time but all in all I am very satisfied with the result. It will be a long post, I estimate about 12 pictures long and that is more or less a record length on this website. I have finished only two pictures and I will take my time to make the other ones because my mouse does not work properly. When I click with the computer mouse, very often that acts as a double click and that makes making pictures a laborsome task because of all the errors that double clicking gives. And when I have to repeat a series of clicks three or four times before it is ok, it will take some time. May be I should buy a new mouse,

Anyway to make a long story short: For years I stayed more or less away from crafting math about integration because it is hard to find a definition that would work always. My favorite way of using Riemann sums could not work always because of the existence of non-invertible numbers in the 3D spaces. And that gave some mathematical fear in my small human mind because path independence came with that way of Riemann summation. All in all it is beautiful math to think about: For example if in 3D you use a primitive to integrate over a closed loop, is it always zero?

So only the first two pictures are posted and I have no idea when all other pictures are finished. Here we go:

That was it, till updates.

It is about time for a small update! Despite all that COVID-19 stuff going round, for myself after all those years I finally tried to put integration on higher dimensional number systems on a more solid footing.
All those years I just refrained from it because you cannot use my favorite Riemann sum approach because of the non-invertible numbers we have in 3D or even higher dimensions.
But now I am trying to finally make some progress and stop avoiding this subject, I find it is utterly beautiful. It has an amazing array of subtle details involved when you have some non-invertible numbers in your integration stuff.
I have no idea when I have finished this rather important detail in my cute theory of higher dimensional complex & circular numbers, so let time be time & in the meantime only post a teaser picture about that lovely integration stuff. In the first lines you see a very familiar integral, likely you have done such calculations in the complex plane. In the case of 3D circular and complex numbers you must (of course) use the multiplication on 3D space to make it all work. Basically you are evaluating (or calculating) three integrals at the same time, just like on the complex plane where you are evaluating two integrals at the same time in your calculation. If you work with a pencil & paper, make sure you have enough paper because all those 3 integrals also have 3 terms in it so your calculations can become quite long…
Here we go:

Ok, let me end this update now. Till updates and for some strange reason you must wash your hands while the proper authorities never point to 3D complex numbers… Till updates.