It’s about time to write this post because the pictures were finished a few days back but I was a bit lazy in the meantime. In this post I only evaluate two line integrals both in some way related to the famous number alpha. And we do it only on the 3D space, there are much more numbers alpha on other spaces but we just do the complex and the circular multiplication in three dimensions. In this post when it comes to the number alpha we mostly need the one property that alpha is it’s own square. Therefore you can break down all powers of alpha into alpha itself, this is very handy when for example you use a power series. As always X denotes a 3D number and one of the integrals we will look at is the exponential of alpha times X: exp(alpha * X). Why do we do this? Well try to find a primitive of the above exponential, that is a bit hard because another property of alpha is that it has no inverse and as such you can’t divide by alpha and so what to do? The second example is integration of the most standard exponential exp(X) along the main axis of non-invertibles: All real multiples of the number alpha. For me this was a surprising result because it all becomes so much more simple. All in all this post is five pictures long but it is in the 550×1500 pixel size so they are relatively long. Ok that is all I had to say and let me now hang in the five pictures:
That was it for this post, thanks for your attention and may be see you in a future post.
A long time ago around the time I started this website I had something known as “The seven properties of the number alpha”. But it was all spread out over two websites because until then I wrote the math just on the other website. But over the years I have advocated a few times to look up that stuff as the seven properties of alpha, so I decided to write a new post with the same title. I didn’t copy the old stuff but just made up a new version. The post is amazingly long; a normal small picture has the size of 550×775 pixels, larger ones I use are up to 550×1100 but now it has grown to 11 pictures of size 550×1500. Likely this is the longest post I have written on math ever. As always I have to leave a lot out, for example doing integration with the involvement of the number alpha is very interesting. During writing I also remembered that e to the power pi times i times alpha, wasn’t that minus one? Yes but we are not going to do six dimensional numbers or hybrids like the 3D circular numbers and replace the reals by the 2D complex numbers. Nope, in this post only properties from the 3D numbers alpha; the complex and the circular one. More or less all the basic stuff is in this post; from simple things like alpha has no inverse to more complicated stuff like the relation with the Laplacian operator. I made a new category for this post, it even has the name “7 Properties of Alpha” so that in the future it will be even easier to find.
Lets hope it is worth of your time and lets hope you will find it interesting.
Figure 01: Alpha is the center of the complex exponential.
Figure 02: You can write X as the sum of two non-invertible numbers.
Ok, that was a long read. I want to congratulate you with not falling asleep. I have no plans for a next post although it is tempting to write something about integration along the line of real multiples of the number alpha.
I didn’t plan on another ‘just a video post’ but I am still working on a new math post on the seven properties of the number alpha. All in all that is going to be one of the longest posts written, that why it takes a relatively long time. So that’s my excuse for another ‘just a video post’.
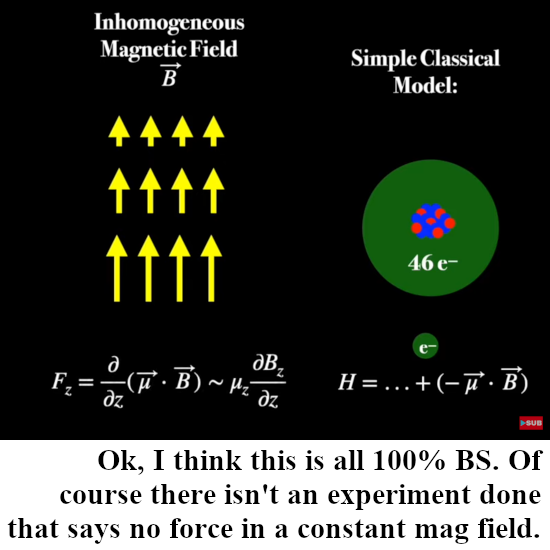
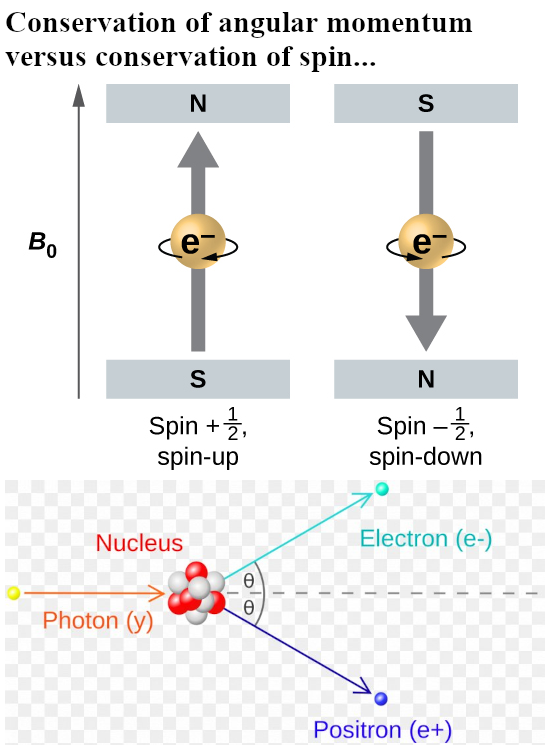
This is another video from Dr. Jorge S. Diaz and again the video is very good made with lots of interesting historical details. In it he shows what Gerlach thought before the experiment was done, that is in the first picture below. In case you did not know it: all that stuff with a varying magnetic field from strong to weak was thought out beforehand. Only the Stern Gerlach guys thought that the silver atoms themselves would act as tiny magnets. That’s why also in the simple math below you see the emphasis on the gradient of the magnetic field. And that brings me once more to an important critisism, not on the video but on the lack of experimental proof that electrons are not accelerated in a constant magnetic field. Ok ok there is still the Lorentz force so that’s easier said then done but it is just missing. Just like there is no experimental proof or evidence that electrons are dipole magnets.
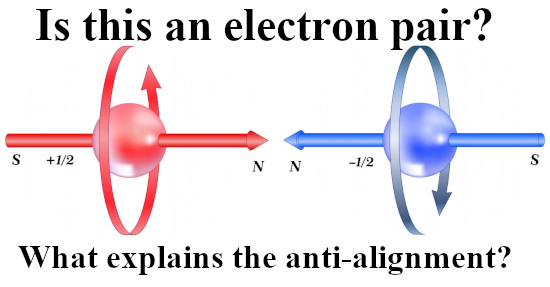
As all video’s on the Stern-Gerlach experiment this one too fails to explain as why tiny magnets would anti-align themselves with the applied magnetic field. After all this raises their potential energy and as such I consider this an important energy problem that you only have if you view electrons as tiny magnets. I remember that back in 2015 when I myself did see this experiment for the first time, it was the fact that the silver atoms would more towards the weaker part of the magnetic field that I just could not understand. But in one or two days I had figured out that if you view electrons as magnetic monopoles, you don’t have weird problems. But back in the time I knew just nothing about electron spin so I had some learning to do.
In the video but also other sources say that it were Einstein himself and Heisenberg who pushed heave for a so called repeated or sequential SG experiment. On may occasions I have argued that such a repeated experiment has never been done in one century of time. And that is strange because if you were successful in this, you would almost one 100% sure have won a Noble prize. And that’s what all the physics people want; a Nobel prize… A repeated experiment would validate the probabilistic nature of electron spin, but it’s just not there and nobody in the physics community gives a shit about that. That’s why so often I say these people are talking out of their neck.
At about 19 minutes into the video Dr. Jorge S. Diaz claims that a repeated SG experiment has been done by Frisch and Segré but that is just plain wrong. In the Frisch-Segré experiment they tried to rotate the spin of an electron. But it failed so to bring this up as an example of a repeated SG experiment is not allowed.
That’s funny: Einstein & Heisenberg pushed for this…
Before I show you the video I want to make a quote from the pdf on the Frisch Segré experiment. The Frish and Segre guys claimed in an article to have observed nondiabetic spin flip. I doubt if that is true but at present day in a lot of physics labs they too think the can flip electron spin in say a diamond nitrogen vacency. But I think that when this happens, they have just another electron with the opposite magnetic charge. This is a WordPress website and I believe they have a ‘quote environment’ hanging around somewhere. So lets try:
Immediately, Heisenberg and Einstein proposed multi-stage Stern–Gerlach experiments to explore deeper mysteries of directional quantization [2]. Ten years later, Phipps and Stern reported the first effort [8], which was unfortunately discontinued owing to Phipps’ involuntary return to the US [2]. A year later, Frisch and Segrè modified the same apparatus by adopting Einstein’s suggestion on the use of a single wire instead of three electromagnets to rotate spin; they also improved magnetic shielding, slit filtering, and signal detection [2]. Despite the use of three layers of magnetic shielding for the middle stage (i.e., the inner rotation chamber), the remnant or residual fringe magnetic field was still 0.42 × 10−4 T (or 0.42 G). Rather than fight the fringe magnetic field further, they took advantage of it. The magnetic field from the wire in the middle stage cancels the remnant field to produce a magnetic null point, around which the field is approximated as a magnetic quadrupole; consequently, they successfully observed nonadiabatic spin flip [9].
In my mind or in my memory the Frisch Segré experiment failed so it is good to be corrected. But all in all you really can’t say that this was a repeated Stern Gerlach experiment. It was trying to flip the spin of an electron. And that while I think the magnetic properties of electrons are just like their electric properties: permanent and monopole. Ok that was it for this ‘just a video post’. Thanks for your attention.
One or two days back this video from Dr. Jorge S. Diaz came out and all in all in it’s kind it is very good. Even for me there is a lot of new stuff in although nothing of the real important things like why an inhomogeneous magnetic field was used: Otto Stern thought that the silver atoms themselves would act like tiny magnets because of the electrons going round the nucleus. I want to remark that using an inhomogeneous magnetic field when it comes to atom sized magnets makes sense, where I draw the line is the blind application to a point like particle like the electron. So all the big hammers were already known to me yet there is a lot of cute stuff in it I had never seen. Things like the first introduction of those quantum numbers from the principle n to the magnetic number m. In the video Jorge Diaz shows once more what the physics people use as the potential energy when a dipole magnet is placed in a magnetic field, you can see that in the picture below.
It is well known that nature loves to minimize the potential energy and here this is the case if both vectors mu and B point in the same direction. In that case the inproduct is a positive number and the minus sign guarantees the minimum of potential energy. Last year I made a picture for repeated use during this year 2024 and in it you see the official version of an electron pair. The Pauli exclusion principle says that the magnetic numbers must differ and as such they must have opposite or anti-parallel spins. The whole problem is of course that if you calculate the potential energy where you view one spin in the magnetic field of the other and use the above expression, you get a positive potential energy. That’s weird since in the science of chemistry it is well known that the electron pair plays an important role in forming atomic and molecular bonds. Here is the sketch of the electron pair once more:
This potential eneregy isn’t minimized.
I made a similar picture for a lone electron that anti-aligns itself with an applied magnetic field:
Beside the potental energy problem, how can this be stable?
As you can see for yourself in the video below, people like Jorge Diaz never even mention that there are severe energy problems. I name that avoiding Crazyland, they only explain the things that sound logical and as soon as it becomes absurd like here with the electron pair, they just don’t talk about that. The weird potential energy problems arise only if you think the electron is a tiny magnet. Since the year 2015 every year I became a bit more convinced that electrons are magnetic monopoles just like they are electric monopoles. All energy problems fade away fast if you do that but hey try to explain that to people like Jorge Diaz! Or for that matter all those other professional physics people out there, those weirdo’s also think that magnetic monopoles do not exist so the taks of explaining things to those people is an almost impossible task. I also combined a few screen shots from the video with people that played some role or contributed to the Stern-Gerlach experiment. For myself I more or less like it that even a guy like Albert Einstein never realized the monopole nature of electron magnetism. But I am also well aware that this can work against me; the physics professionals will likely think that if Albert didn’t see it, it can’t be true and as such for themselves they have once more confirmed that magnetic monopoles don’t exist…
And finally the video, again in it’s kind it is a very good video:
A lot more could be said or written but lets not do that and may I thank you for your attention.
If you view the interger points of the plane equipped with the elliptic complex multiplication as prime numbers or composites, you have found a good basis to predict or calculate how much of such integer solutions there are. This problem is closely related to the number of integer points on a circle, I am sure you can find enough internet resources of that problem. I decided to take a deeper look into this because of a video on the Eisenstein primes, those Eisenstein primes and integers look a lot like my own elliptic complex integers. But the Eisenstein numbers are defined on the standard complex plane while I modified the way the multiplication is done via a tiny change to i^2 = -1 + i. So that now ‘rules’ my plane with elliptic complex numbers and one of the nice properties is that i^3 = -1 while for that Eisenstein stuff you get +1. So the Eisenstein numbers are more a way of say the split complex numbers. Lets start with the video that I considered to be remarkable good:
For me it was all brand new because to be honest I never ever studied the Gaussian integers and how that gives rise to a unique way of factorizing them. But now I had to solve the problem for my own 2D elliptic numbers I have to say that yes it is beautiful once you grasp what’s going on.
A well known fact from the Gaussian integers is that the number 5 is now no longer a prime number because it can be factored into 2 + i and 2 – i. On the complex elliptic numbers it is 7 that is the smallest integer to have that same fate as 5 on the Gaussian integers. This post is mostly about the two factors that factorize 7, I named them p and q and the interesting thing is they are each others conjugate. But the number 3 is also no longer a prime so all in all for a person like me who dislikes algebra so often for so many years, it was all in all a nice patch of math to understand.
This post is 8 pictures long, each 550×1250 pixels and on top of that two extra figures are addes. So what more do you want? I kept the stuff as less technical as possible while hoping that if you want to dig a bit deeper you can do that for yourself now. So lets start the picture thing:
Figure 1: Seven is the smallest number that has two conjugate prime factors.Figure 2: These are the 18 integer solutions to det(z) = 49.
Last week for the first time I decided to take a look at that so called muon g-2 experiment. Nothing from the preprint archive, no just a little bit lazy watching a few video’s. That’s why in this post I have 3 video’s for you.
It soon dawned on me that the Fermilab experiment was a bit strange. They use the Lorentz force to let the muons go round while the spin stays horizontal. Now muons are cousins of the electrons and the official theory is that they are tiny magnets just like electrons. And as so often observed, the professional physics people only say things that sound or look logical. All weird stuff that comes from what I name Crazyland is just not mentioned. Things from Crazyland are of course the electron pair and how is that configuration even possible? An old experiment done in 1922 was the Stern-Gerlach experiment and there too do the experimetalists use a vertical magnetic field. (It could be that in the original experiment the field was horizontal but that’s not important for our discussion here.) What’s interesting is that if you read or see one hundred explanations for the Stern-Gerlach experiment it is always the official version that the spins align vertical or anti-vertical. The anti-vertical stuff is also a thing from Crazyland; why would an electron turn against the magnetic field and as such gaining potential energy? But we skip that because the relevant obervation is that if you see a 100 explanations, the electrons always align in a vertical manner.
Here you see a screenshot from the first video:
In the above picture it is nicely shown what the professionals have made of it; the Hamiltonian clearly says that if electrons anti-align they gain potential energy but they never talk about that. And the expression for how an electron is accelerated in an inhomogeneous magnetic field is basically the same as say in gravity. The potential energy in a gravity field is mgh and if you differentiate into the vertical direction, that is in the direction of h, you are left with mg and that’s the force due to gravity. I think this is BS because I think electrons (and muons) are magnetic monopoles. As such they should be accelerated by all kinds of magnetic fields and I myself don’t have experimental evidence for that. But the professional physics people don’t have evidence for their claim that in a homogeneous field electrons don’t get accelerated. Since 2014 I never stumbled upon any experimental result in that direction. It’s about time to go to the first video. It is from a channel named Abide By Reason and that’s a very good name only he doesn’t do it. There’s not much reason found but it’s the official explanation for the SG experiment.
Now for the Fermilab muon g-2 experiment: Despite the vertical magnetic field for some strange reason non of those muons change their magnetic orientation. Even stronger, the folks from Fermilab are so über-ultra-mega smart that they know that after one rotation in the ring, the muon spin has furned about 12 degrees more… Of course nobody explains why that spin stays horizontal even though the vertical magnetic field has a strength of about 1.5 Tesla. But in this experiment they need that spin is horizontal stuff so like all physics people at some time they have to talk out of their neck. Physics is the science of talking out of your neck while maintaining that you are a five sigma kind of science.
Where is the torgue on the muon gone? Why is it neglected in the explanation?
The above screenshot is from a lady that has a video channel named “Think Like A Physicist” and sometimes that’s a good idea but when it comes to electron spin you better try to think as a logical person. Video title: Measuring Muon g-2. Link used: https://www.youtube.com/watch?v=IHgaapwwLN0
Now the lady that thinks like a physicist claims the magnetic field is vertical but in the last 9 years I have seen all kinds of weirdo’s making all kinds of claims when it comes to this or that. So again avoiding difficult to read pdf’s from the preprint archive there was indeed a video from Fermilab herself validating the magnetic field is vertical. Please remark that from the outside when you look at that ring the Fermilab got from Brookhaven, it is hard to see what kind of magnetic field is inside. The video is about 3 minutes long. Video title: Muon g-2 Experiment Shimming. Link used: https://www.youtube.com/watch?v=4HlKN0rfdKA
That was it for this post, in this post we had zero people explaining that quantum states like electron spin are just so fragile. But we had some people just ignoring muon spin doesn’t flip even when it’s going round and round in some Fermilab experimental setting.
Likely the next post is about prime numbers in the plane of elliptic complex numbers. So it’s just some two dimensional stuff with numbers and integers. A lot of prime numbers like 7 are not elliptic primes. They can be factored inside the elliptic plane by two smaller primes. So that’s all very interesting but also time consuming but all in all in a week or two it should be finished.
In the picture below you can see what natural primes survive the elliptic onslought. They are the ones with ellipses that don’t have integer solutions.
Lately I added a bunch of sine functions and I wondered what the maximum was. And to be honest I had no idea, in math that is pretty normal otherwise you would not search for such answers. The questions you can answer instantly are often much more boring and often don’t add much value or insights. So what was I looking at? Well take the sine function, lets write it as sin(t). Make a timelag of one unit or if you want a translation and that’s sin(t – 1). Proceed in taking time lags like sin(t – 2), sin(t – 3) and so on and so on and add them all up. The question is: Can you say something about the maximum value that this sum can take? And no, I had no idea about how to approach this problem.
The interesting detail is of course that this sum of sines does not seem to converge or diverge in any significant way. You can check that for yourself in for example the DESMOS package, just type the word sum and you get the sigma symbol for a summation. I like the package and in case you have never seen it, here is a link: https://www.desmos.com/calculator?lang=en.
As far as I know this problem has no or little math meaning, it is just some recreational stuff. But if you in your life had the honor of calculating a bunch of Fourier coefficients again and again, you know that the summation of sines and or cosines and or complex exponentials can have very tricky convergence questions. Now with my little sum of sine time lags we don’t have any convergence at all, the funny thing is it also does not diverge.
This post was meant to be short but as so often it grew to five pictures long and on top of that there are three extra figures added to the mix. It’s all pretty simple and not deep complicated math that as so often is very hard for human brains to digest. Have fun reading it.
Figure 1: Yep, this is not a periodic function.Figure 2: Positive interference leads to larger amplitudes.Figure 3: Oh oh some stupid typo’s with the number 50…
At the end of this post I want to remark that I framed the question for some finite sum of sines. That is because I wanted to avoid all things related to taking a supremum and stuff like that. Look at Example 1 above, here of course the maximum value of the two sines is not 2 because there is no real solution to this, but of course the supremum is 2 because you can come arbitrarily close to 2. Of course in Example 3 I wanted to know the sup and the inf of the amplitudes, but I framed the question in a finite sum of sines anyway.
Ok that was it for this unclassified post. If you want you can think a bit about sums of sines and if you get bored of that you can try to figure out what an electron pair is if the Pauli exclusion principle says it must have opposite spins… Thanks for your attention and see you in the next post.
This is another very short post, the main text is 2 pictures and there is an additonal Figure 1 added. It is about the impossibility of having both spin and angular moment conserved in the electron-positron pair creation process. This is under the assumption that electrons are actually spinning and that this spinning causes the official version of electron spin: the tiny magnet model. Of course there is nothing spinning, back in the time Wolfgang Pauli himself calculated that even if you concentrate all the electric charge of an electron on it’s ‘equator’, it must spin so fast that this is a huge multiple of the speed of light. A long time ago I did such a calculation myself, it is not very hard to do but I skipped it in this because that calculation has nothing to do with the content of the post. So you can easily do that yourself, after all it is just some advanced high school physics and if you do that the answer will of course depend strongly on how large you think the electron is if you view it as a tiny billiard ball. The word ‘spin’ is a terrible wrongly chosen word to describe the magnetic properties of the electron. I have wondered so often as why the physics people think year in year out that the electron is a tiny magnet while you really do not need much brain power to see that this is nonsense. Beside all those fundamental energy problems there are also problems with the above mentioned conservation laws. The fact we have today so many people from the physics community talking about ‘the spinning electron’ is caused in part by that original stupid choice to name it ‘spin’. After all this word strongly suggests that we are dealing with tiny magnets, every electron must be a tiny bipolar magnet while if you view them as magnetic monopoles you don’t have all these weird energy problems. In case you are new to this website: I think that electrons are magnetic monopoles, just like their electric charge, and furthermore this magnetic charge is permanent and as such it is impossible to flip the spin of an electron. And if you are from the physics community yourself, may be you need to vomit from the idea that electrons are not tiny magnets. Or may be you pity me because I am a middle aged man and you think I want to save physics or the wider community known as humankind from wrong doing when it comes to electron spin. Well I have to disappoint you: I don’t give a shit about such stuff, ok in the beginning I did but after a few years I realized that likely physics will be trapped a few centuries longer before they start using logical thinking when it comes to electron spin.
In the two pictures below I also experiment a bit with using other backgrounds, here you see something like a big hand made with some generative AI video thing. May be it is time to replace my old background made with my old Windows XP computer by some fresh stuff.
This intro is getting far to long because I wanted this post to be short. So let me hang in the pictures and here we go:
In Figure 1 below all you see are two images I downloaded from the internet while using the search phrases as written above. You just never see those spinning arrows if you search for electron-positron pair creation. It is as so often: As soon as we get into crazyland, the physics people just don’t talk about it.
Figure 1: Never spin ‘explained’ via arrows in pair creation.
This post is a bit deeper when it comes to the math side, I think you better understand it if you already know what such a Cauchy integral representation for the standard complex plane is. I remember a long long time ago when I myself did see this kind of representation for the first time, I was completely baffled by this. How can you come up with a crazy looking thing like this? But if you look into the details it all makes sense and this representation is the basis for things like residu calculus that you can sometime use to crack an integral if all more easy approaches fail. In most texts on the standard complex numbers (with standard I mean that the imaginary unit i behaves like i^2 = -1 whereas on my elliptical version the behavior is i^2 = -1 + i) it is first shown that you can take such integrals over arbitrary closed contours going counter clockwise. If the function you integrate has no poles on the interior of that contour, the integral is always zero. I decided to skip all that although if you want, you can do that of course for yourself. I also skipped all standard proofs out there because I wanted to craft my own proof and therefore in this post we only integrate over the ellipses and nothing else. Another thing to remark is that this is just a sketch of a proof, a more rigor approach would make the post only longer and longer and I think that people who are interested in math like this are perfectly capable of checking any details they think that are missing or swept under the carpet. For example I show in this post the important concept of ‘radial independence’ but I show that only for a very simple function g(z) = 1. It’s just a sketch and sometimes you have to fill in what is missing yourself. Sorry for being lazy but now already this post is 5 and a half pictures long so that’s long enough.
It also contains two extra figures and may be I will write a small appendix related to figure 1. But I haven’t done that yet so below is the stuff and I hope you like it.
Figure 1: The elliptic complex exponential and it’s coordinate functions.Figure2: This is just some arbitrary point a and some arbitrary radius of 1/16.
Ok, all that is left is an appendix where I give a third parametrization of the elliptic complex exponential. It is just some leftover from some time ago when I wondered if the two coordinate functions might some some time lags of each other. And yes, they are. In the case of these elliptic complex numbers the time lag is one third of the period.
Another short post, this time again on the totally crazy so called bonding and non-bonding pairs in theoretical chemistry. It is one of the many energy problems that come along if you want electrons to be tiny bipolar magnets. And if you view the electrons as magnetic monopoles, in that case all of a sudden you don’t have these kind of weird energy problems.
Lets dive into it, this post is 3 images long and here we go:
That’s more or less all I had to say today, if you view the magnetic properties of electrons as monopole magnets just like their electric properties the standard electron pair becomes the lowest (potential) energy state. Before I close this post let me quote from a wiki an interesting detail about the non-bonding electron pairs: they have a tendency to be outside the so called ‘bonding region’ between atoms in molecules. Once more this only makes sense when electron carry a monopole magnetic charge.
In theoretical chemistry, an antibonding orbital is a type of molecular orbital that weakens the chemical bond between two atoms and helps to raise the energy of the molecule relative to the separated atoms. Such an orbital has one or more nodes in the bonding region between the nuclei. The density of the electrons in the orbital is concentrated outside the bonding region and acts to pull one nucleus away from the other and tends to cause mutual repulsion between the two atoms. This is in contrast to a bonding molecular orbital, which has a lower energy than that of the separate atoms, and is responsible for chemical bonds.
That’s it, see you in some other future post or enjoy some old posts on say the 4D complex numbers because they are beautiful and that is something we cannot say about the behaviour of the average physics professor with their weird fixation on electrons as tiny magnets…
