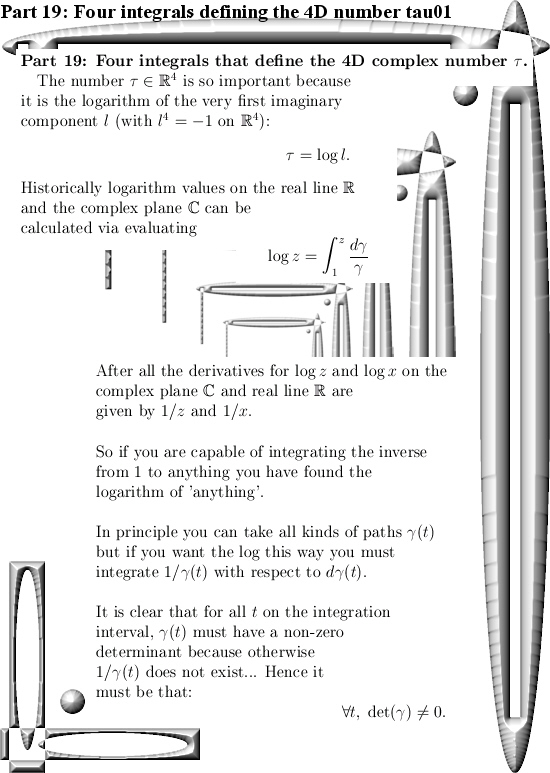
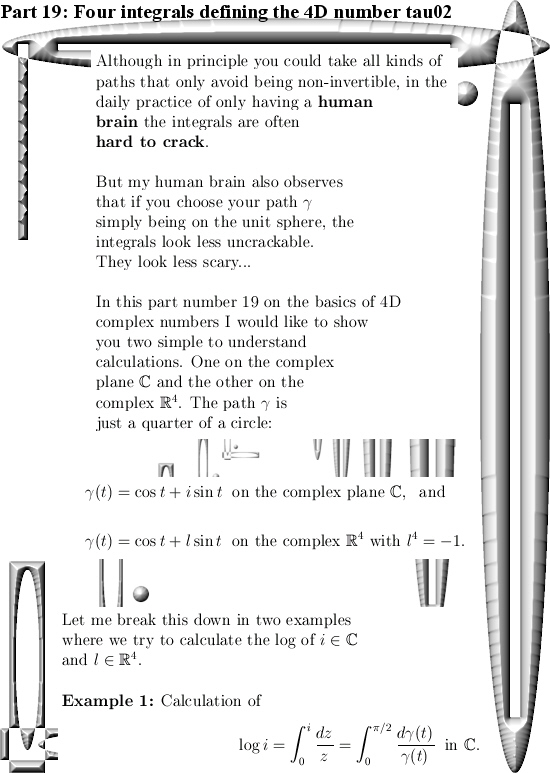
Recently I am working on part 20 to the basics of the 4D complex numbers. Ok ok if you need 20 parts to explain ‘the basics’ how basic is it you can ask yourself.
You can argue long and short on this: are fresh Cauchy integral formula’s really ‘basic stuff’? I don’t know how a democratic vote among professional math professors would fall down.
Anyway, an important property of the determinant of 4D complex numbers is the fact that the determinant is always non-negavite. At least it is zero and at those points in space we have found a non-invertible number.
In part 20 on the basics to 4D complex numbers we will look when the eigenvalues of 4D complex numbers vanish; at those points the stuff is non-invertible & that is what we will be hunting on part 20.
In the next picture you see a difficult to understand inequality & the teaser question is:
Can you prove this inequality via math methods that do not use 4D complex number theory at all?
If so, you should definitely pop up a second pint of perfect beer on a late Friday evening.

Ok, that was it. Till updates in part 20 where we try to find all non-invertible 4D complex numbers in a not too difficult way.