Monthly Archives: February 2021

The last Fermat theorem (positive version) versus the number 1.

Last Fermat theorem, Uncategorized

This is a short post; just over 3 pictures long. We make a few calculation on the ring of integers modulo 35. Of course that is a ring and not a field because 35 has two prime factors namely p = 5 and q = 7. These two prime factors form so called divisors of zero, that means that pq = 35 = 0 inside the ring of integers modulo 35.
Because the two prime factors have this property, that has all kinds of simplications when it comes to expanding (p + q)^n inside this ring. That is what I name the ‘positive version’ of the last theorem of Fermat: The ring of integers modulo 35 is a simple number space where the last theorem of Fermat is possible, here we again have 12^n = (5 + 7)^n = 5^n + 7^n.

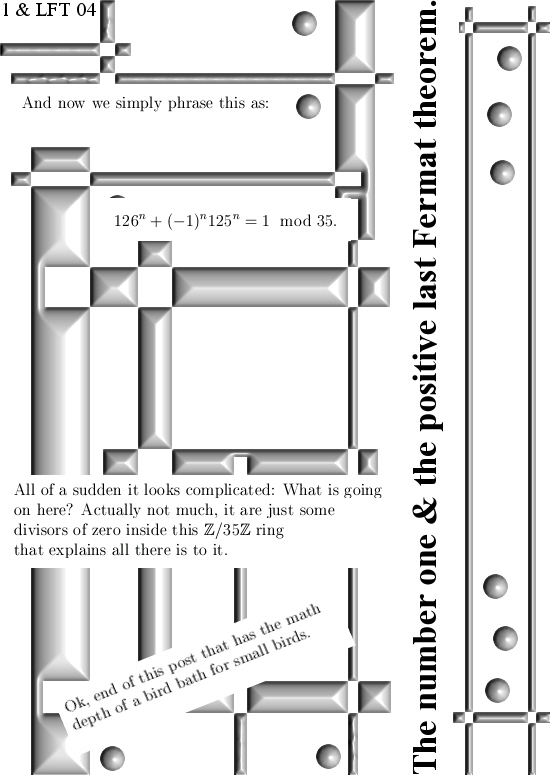
In this post I use the fact that the prime numbers 5 and 7 are also relatively prime and as such you can make a linear combination of them to get the number 1. And once you have the number 1 you can use them as a basis for the entire ring of integers modulo 35. But if you have a healthy brain, likely you will remark that it is far more easy to just use the counting numbers 1, …, 35 or just 1 to craft such a basis… So I understand that you might think I am crazy to the bone. Of course I am crazy to the bone but there is a goal in this utter madness. Take for example 3*5 – 2*7 = 1, this is one possibility to form the number 1 as a linear combination of 5 and 7. Since both terms contain one of the pairs of divisors of zero as a factor, this linear combination allows for a positive last theorem of Fermat decomposition: For a natural numbers n we have that: (15 – 14)^n = 15^n + (-1)^n*14^n = 1.
Although such expressions are very cute looking, it has no significant math depth anyway. All in all this post it totally unimportant because it is all so simple. The post upon the 3D Gaussian integers is far more important because there it was possible to write the number 3 as a linear combination of two 3D Gaussian integers. As such for the first time in about 350 years it was the first serious counter example against the last theorem of Fermat because that number 3 was just on the line of integers. It was not something inside some modulo number space or so, that was the real deal for the first time in 350 years.

Will math professors react on such a finding? Of course not. For example they would reason before the finding that if you can’t use 3D complex numbers to find only one significant result in algebra or number theory, that proves 3D complex numbers are useless.
And after the counter example to the last fermat theorem? Well math professors are the most smart people on earth, they are higly agile and adeptable and now the reasoning will likely be something like: In the entire history of mathematics nobody has ever used 3D Gaussian integers. This all is so far fetched that this is not serious math…

Well that is how they are and there is no changing that kind of behavior I just guess. Anyway enough of the blah blah blah. The post is just over 3 pictures long, has no mathematical significance anyway and I hope you have some fun reading it.

For odd n you get a minus sign, for even n you get a plus sign.
It is not significant math, but it sure looks very cute!

It is now one hour after mdinight so it is time to hit that button named ‘Publish website’. Live well & think well my dear reader. See you in the next post or so.

Another counter example to Fermat’s last theorem using 4D complex numbers.

4D complex numbers, Last Fermat theorem

All in all I am not super satisfied with this post because the math result is not that deep. Ok ok the 4D complex numbers also contain non-invertible numbers, say P and Q, and these are divisors of zero. That means PQ = 0 while both P and Q are non-zero. And just like we did in the case of 3D circular and complex numbers because of the simple property PQ = 0 all mixed terms in (P + Q)^n become 0 and as such: (P + Q)^n = P^n + Q^n.

In the space of 4D complex numbers an important feature of the determinant det(Z) of a 4D complex number Z is that it is non-negative. As such there is not a clear defined layer between the part of the number space where the determinant is positive versus the negative part. During the writing of this post it dawned on me that Gaussian integers in the 4D complex space always have a non-zero determinant. As such the inverse of such a Gaussian exists although often this is not a Gaussian integer just like the inverse of say the number 5 is not an integer. A completely unexpected finding is that the 4D complex fractions form a field…

That made me laugh because the professional math professors always rejected higher dimensional complex numbers because they are not a field. For some strange reason math professors always accept or embrace stuff that forms a field while they go bonkers & beserk when some set or group or ring is not a field. This is a strange behavior because the counter examples that I found against Fermat his last theorem are only there because 3D and 4D numbers are not a field: there are always non zero numbers that you cannot invert.
As such a lot of math professors are often busy to make so called field extensions of the rational numbers. And oh oh oh that is just soo important and our perfumed princes ride high on that kind of stuff. And now those nasty 4D complex numbers from those unemployed plebs form a field too…
I had to smile softly because 150 years have gone since the last 4D field was discovered, that is known as the quaternions, and now there is that 4D field of rationals that are embedded into something the cheap plebs name ‘4D complex numbers’? How shall the professional math professors react on this because it is at the root of their own behavior over decades & centuries of time?

Do not worry my dear reader: They will stay the overpaid perfumed princes as they are. Field or no field, perfumed princes are not known to act as adult people.

After having said that, this post is only five pictures long all of the ususal size of 550×775 pixels. For myself speaking I like the situation on the 3D numbers more because there you can easily craft an infinite amount of counter examples against the last theorem of Fermat.
Ok, here we go:

Yes I have to smile softly: all this hysteria from overpaid math professors about stuff being a field or not. And now we are likely into a situation where the 4D complex numbers are not a field but the space of 4D complex rationals is a field…

Will the math professors act as adults? Of course not.
Ok, let’s end this post because you just like me will always have other things to do in the short time that we have on this pale blue dot known as planet earth. Till updates.

On plasma instability in nuclear fusion reactors.

Magnetism

The next post will be math again; more of the ‘positive’ last theorem of Fermat stuff. This time on the 4D complex numbers. In case you missed it, I found 3D Gaussian integers, say A and T and if we sum them up, say S = A + T, in that case S^n = A^n + T^n. The last theorem of Fermat says this is not possible for ordinary integers but in higher dimensional number systems it is not that hard to find.

Last week the UK Royal Institution had a new video out about nuclear fusion. At first I wanted to comment on it but it is more or less the same video as the one from four years back so I skipped that. Anyway in the UK they still have a workable nuclear fusion reactor and all those years I just thought they put it on just a few seconds every now and then because of the plasma instabilities. I was wrong, the latest video says it is because they do not have superconducting magnets, the magnets they use are made from ordinary copper wiring and that produces a lot of heat and that is the explanation for the short operational times.

But today I came across another video with news about nuclear fusion and there it was claimed that Korea succeeded into more than doubling the operational time of their fusion vessel! From 8 seconds to 20 seconds!
So I feel the need to once more explain how these plasma instabilities form using the simple idea that electrons are not magnetic dipoles but magnetic monopoles. I am well aware of the fact that people like Ian Chapman (he is in the UK video from the RI) start vomiting by the idea that electrons are magnetic monopoles, or may they consider it a funny joke from one of those dumb persons in the so called ‘general audience’. From my side of the story I will not poke fun about Ian Chapman because it is morally rejectable to poke fun at people who are mentally handicapped…;)

The Koreans used an Internal Transport Barrier…

In my view where electrons are magnetic monopoles there are two kinds of electrons: those with a ‘north pole’ magnetic charge and the ones with a south pole version of magnetic charge. Needless to say they have the same electric charge.
Ok, these electrons are in a plasma inside a torus shaped vessel of a fusion reactor and the magnetic field gets turned on. What will happen?

Very simple: The electrons get accelerated into the direction of the magnetic field lines. Therefore if the north pole charged electrons go say clockwise, the south pole charged electrons will go anti clockwise.

Since these electrons are constantly accelerated by the magnetic field that is supposed to contain them, they will cluster together in streams just like water going downhill. Water going downhill does not do that every water molecule on it’s own; it forms stream of water that accumulate in size until you get rivers… The electrons in the plasma simply do the same; if an individual electron finds itself back in an environment where there are lots of other electrons moving into the same direction, it will stay there and get more and more accelerated all of the time.

So over time there will be larger and larger streams or rivers of electrons and because there is a lot of kinetic energy in those streams, if the two streams interact it will be very violent.

That is the explanation in a nuttshell, I know that professional physics professors will laugh about me thinking I am the retarded one. I don’t care that much about that, after all they are too stupid to make use of 3D complex numbers so who is the retarded here at the end of the day?

Fantastic, this will save humanity from climate change…

An interesting detail in those plasma vessels that are shaped like a torus is that in the middle the magnetic field seems to be stronger. That would be an explanation as why the plasma does not blow into the wall at the very beginning. But if you would ask the plasma professors as why the walls are spared for a short time, those people likely have not a clue what soever.
The JET nuclear fusion vessel operates only for short amounts of time but already in these few seconds there are violent outbursts of the plasma against the walls of the vessel. Here is a screen shot from the video where Ian Chapman expains his wisdom at 20 minutes into that video.

It is important to know it gets unstable within a few seconds of operation…

These people chase a dream that is impossible. And at the same time when I demand proof that actually the electrons is a magnetic dipole those mentally handicapped people always stay silent. The silence proves the mentally handicapped thing and the video’s they spit out prove that they are severely overpaid and will never come to their senses.

No comment.

All that is left is to place the two video’s into this website. Because the video on fusion news is so short I place that first.

The Korean stuff is found at 5.30 minutes into the video

And here is the thing from the UK, by the way how is your Brexit going? The important details are at 23 to 25 minutes into that video.

Ok, that was it for this post. All those nuclear fusion plants will blow up but I just don’t care. See you in the next post.

Electrons can’t be magnetic dipoles; yet discontinuation of the magnetic pages…:(

Magnetism

After giving it a few months of thought I decided to discontinue the magnetic pages on the other website. For five years I collected reasons as why it is impossible that electrons are magnetic dipoles. Yet it never took off, if I do an internet search on ‘electrons cannot be magnetic dipoles’ weirdly enough it is a result from this website and just nothing from the files on magnetism.

As a comparison if you search for 3d complex numbers the results from the other website still pop up even dating back to the year 2012…

I had to conclude it just does not work and I better use my time for other hobby’s because there is little use in writing every month the stuff found down if nobody is reading it. That is a waste of time.

Of course from the get go five years back I understood it would be a hard sell to explain that it is impossible that electrons are magnetic dipoles to the community of physics. After all there is zero experimental evidence for the electron being a magnetic dipole so it must be some widespread belief not rooted into experimental proof.

There are more explanations possible as why the magnetic pages never took off; for example it could be that on average the physics professors are much more stupid compared to math professors. They are just too dumb or may be just too arrogant to give it a second thought.

Another possible reason for the failure of the internet search engines could be that in general people are just much more interested in math and not so much in physics. A clue to that could be the extreme popularity of a channel named ‘Numberphile’ on youtube. The guy that runs that channel has much more channels like stuff on physics but that seems to be far less popular.

Whatever it is, I have decided to put an end to it so no more updates in the magnetic pages forever. Here is the last update:

14 Jan  2021: Reason 87: There is ‘too much’ symmetry in the universe.

Yes, over a timespan of five years 87 reasons found while zero response in the internet search engines. In this last reason I quote some words from Gerard ‘t Hooft who is wondering why we only can measure two states for the electron. Well Gerard might have gotten his Nobel prize, but if he keeps on thinking the electron is a magnetic dipole without any fucking experimental proof for that he is a neglectable cognitive quantity.

Inside physics there are many more people that clearly are not very helpfull, take that arrogant piece of shit like a Edward Witten. Always 100% arrogant but just too stupid to understand it is plain impossible for the electron to be a magnetic dipole. How can a guy like Edward explain the results of the Stern-Gerlach experiment while the electron is a magnetic dipole? In my view this only shows that Edward Witten is a mathematical imcompetent person…

But hey I do not want to sound like a sour old man, after all it is with great pleasure but just a little smile on my face that I can write down words like ‘Edward Witten is a mathematical incompetent person’. Please do not think I am driven by hatred, I am not.

Ok, one more clue as why electrons cannot be magnetic dipoles. It is named the Stark effect and this effect is the application of an electric field and that seems to split the spectrum of the photons emmited. But it looks just like the shift in the spectrum of when a magnetic field is applied.
Here is a picture of the spectral shift under application of an electric field:

Oops, that looks just like magnetic splitting…

The above picture is a screen shot from a video source I will not link to.
If those physics people will never grow into adulthood, why take the time and trouble to place correct links and so. Arrogant weirdo’s like Edward Witten from the string theory crazies will only do their own overpaid nonsense…

In life it is important not to get consumed by hatred in the long run because always living in hatred is bad for your health. So you confine you deep hatred to only small attacks that make a bit of fun. After that you shake the hatred off like it is just some water.
And say for yourselve: The next picture shows my bike computer and it says 80 thousand kilometers done. I mean that’s life and listening to the words of Edward Witten is not much of a life…

Wow that is about twice circuling the earth if there would be a bicycle path around our beloved globe. In the next picture I made a cube from it:

And in the last picture also a cube about the results in the previous post where I found some cute results in 3D complex and circular numbers that can be classified as positive Fermat theorems. Now will a piece of shit like Edward Witten ever understand it? I do not care what that weirdo thinks.

But after 350 years of zero progress on the last Fermat theorem, I hope I made a tiny and very small contribution that will survive.

All that modulo stuff is hard to read. So read the previous post!

Ok we are at the end of this post. Till updates.