Monthly Archives: April 2019

Using the Cayley-Hamilton theorem to find ‘all’ multiplications in 3D space.

3D complex numbers, CR equations, Matrix representation, Uncategorized

It is a bit vague what exactly a multiplication is, but I always use things that ‘rotate over the dimensions’. For example on the 3D complex space the imiginary unit is written as j and the powers of j simply rotate over the dimensions because:

j = (0, 1, 0)
j^2 = (0, 0, 1) and
j^3 = (-1, 0, 0). Etc, the period becomes 6 in this way because after the sixth power everything repeats.

In this post we will look at a more general formulation of what the third power of j is. The Cayley-Hamilton theorem says that you can write the third power of 3 by 3 matrices always as some linear combination of the lower powers.

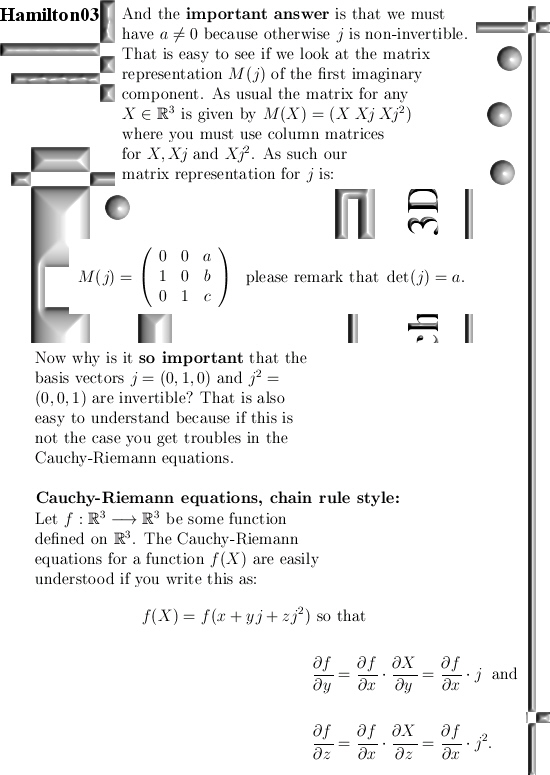
That is what we do in this post; we take a look at j^3 = a + bj + cj^2. Here the a, b and c are real numbers. The allowed values that j^3 can take is what I call the ‘parameter space’. This parameter space is rather big, it is almost 3D real space but if you want the 3D Cauchy-Riemann equations to fly it has to be that a is always non zero. There is nothing mysterious about that demand of being non zero: if the constant a = 0, the imaginary unit is no longer invertible and that is the root cause of a whole lot of trouble and we want to avoid that.

It is well known that sir Hamilton tried to find the 3D complex numbers for about a full decade. Because he wanted this 3D complex number space as some extension of the complex plane, he failed in this detail and instead found the quaternions… But if the 3D numbers were some extension of the 2D complex plane, there should be at least one number X in 3D such that it squares to minus one. At the end I give a simple proof why the equation X^2 = -1 cannot be solved in 3D space for all allowed parameters. So although we have a 3D ocean of parameters and as such an infinite amount of different multiplications, none of them contains a number that squares to minus one…

I gave a small theorem covering the impossibility of solving X^2 = -1 a relative harsh name: Trashing the Hamilton approach for 3D complex numbers. This should not be viewed as some emotional statement about the Hamilton guy. It is just what it says: trashing that kind of approach…

This post is 7 pictures long, each of the usual size of 550×775 pixels.

Test picture, does jpg upload again?












Sorry for the test picture, but the seven jpg pictures refused to upload. And that is strange because they are just seven clean jpg’s. Now it is repaired although I do not understand this strange error.

Anyway have a cool summer. Till updates.

The supersized electron, can you accelerate one cubic cm of this stuff with a magnetic field?

Magnetism

This post is a continuation of Reason number 50 as why electrons cannot be magnetic dipoles as found on the other website. I published nr 50 in 2017 on 14 Oct. In that nr 50 Reason I tried to estimate the gradient of an inhomogeneous (non constant) magnetic field. It was just a rough estimation so you can have all kinds of critisism on it, but the gradient needed in the magnetic field was so huge that we safely can conclude that electrons cannot be accelerated by non constant magnetic fields.

Back in the year 2017 I more or less stated that universities are never very helpful. I joked that the word cooporation was not found in their dictionary. So now about 18 months later this seems to be true, why is that? Well all universities are relatively formal structures, most things go along some kind of protocol. For example when I would try to get a research job for the study of magnetic domains (because I think magnetic domains have surplusses of either one of the spin variants, so every magnetic domain is a magnetic ‘monopole’ on the domain level), that likely would not be possible. Because everything goes in such a formal manner likely I have to start as a first year student of physics, slowly climb the ranks and that’s it because ‘we cannot make an exception’. And from the university this is rather logical; if they give in to one weirdo that think that electrons cannot be magnetic dipoles, next comes along another crazy person that wants to study more homeopathic medicines or whatever what.

Ok, what are we looking at in this post? I simply view the electron as some kind of massive small sphere with a diameter of 10^-16 meter and as such estimate the density or the mass per cubic meter.

Without trying any kind of calculation, try to accelerate such an object with an inhomogeneous magnetic field…

It is three pictures long so this is a short post although the numbers are impressive. Picture sizes all 550×775 pixels.

Ok, this is what I had to say on the impossibility of accelerating magnetic dipole electrons in any meaningful amount while using inhomogeneous magnetic fields… See you in the next post.

The Cayley-Hamilton theorem neglected for 25 years?

3D complex numbers, Matrix representation, Uncategorized

That is strange, if you don’t know the Cayley-Hamilton theorem; it is the finding that every square matrix A, if you calculate the characteristic polynomial for the matrix A it is always zero. At first this is a very surprising result, but it is easy to prove. It’s importance lies in the fact that in this way you can always break down higher powers of the matrix A in lower powers. In the study of higher dimensional complex and circular numbers we do this all the time. If in 3D space I say that the third power of the imaginary component is minus one, j^3 = -1, we only write the third power as a multiple of the zero’th power…

In this post I will give two simple proofs of the Cayley-Hamilton theorem and although in my brain this is just a one line proof, if you write it down it always gets longer than anticipated.

At the end I show you an old video from the year 1986 from the London Mathematical Society where it is claimed that the CH theorem was neglected for 25 years. Now Hamilton is also famous for having sought the 3D complex numbers for about a full decade before he gave up. And I still do not understand why Hamilton tried this for so long but likely he wanted to include the imaginary unit i from the complex plane in it and that is impossible. Or may be he wanted a 3D complex number system that is also a field (in a field all elements or numbers that are non-zero have an inverse, in algebra wordings; there are no divisors of zero). A 3D field is also impossible and in this post I included a small proof for that.

Furthermore in this post at some point may be you read the words ‘total incompetents’ and ‘local university’. You must not view that as some emotional wording, on the contrary it is a cold clinical description of how math goes over there. So you must not think I am some kind of frustrated person, for me it is enough that I know how for example to craft a 3D complex number system. If they don’t want to do that, be my guest. After all this is a free country and we also have this concept of ‘academic freedom’ where the high shot math professors can do what they want.

And what is this ‘academic freedom’ anyway? If for example unpaired electrons are never magnetically neutral but electron pairs always are magnetically neutral, can the physical reality be that electrons are magnetic dipoles? Of course not, that is a crazy idea to begin with. But 97 years of academic freedom since the Stern-Gerlach experiment have never ever brought any meaningful understanding of the magnetic properties of the electron. If it acts as a magnetic charge and you say it is not a charge it is easy to understand how you can fool yourself for about one century of time.

This post is seven pictures long although the last picture is empty.
The two proofs of the Cayley/Hamilton theorem is how I would prove such a thing but good theorems always have many proofs. All pictures are of the size 550×775 pixels.













Why is the seventh picture without math?

Here is the old video from 1986 where it is claimed the Cayley-Hamilton theorem was neglected for about 25 years. Oh oh oh what a deep crime. But the human mind is not made to produce or understand math, so in my view 25 years is a short period of time if in the good old days math professors were equally smart as the present day math professors. The title of the video is The Rise and Fall of Matrices.

Matrices saved my life from crazy math professors.

Ok let me leave it with that an not post a link to the top wiki on the Cayley-Hamilton theorem where all kinds of interesting proofs are given. Till updates my dear reader.