Monthly Archives: August 2019

The two self-conjugate planes for 3D circular and complex numbers.

3D complex numbers, Matrix representation

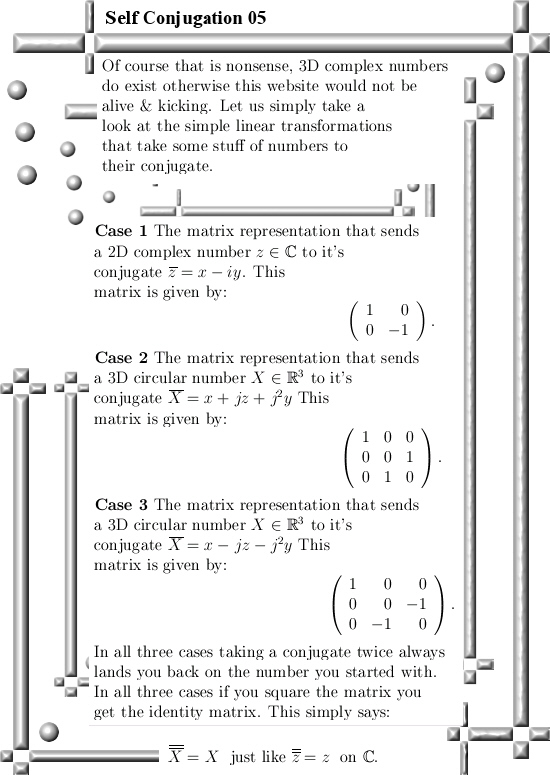
This is another lightweight easy going summer update. It is about matrix representations and how to find the conjugate of a 3D complex or circular number. I use the case of the complex plane of 2D conplex numbers to show that conjugation is not some silly reflection just always but rather simple will always be the upper row of a proper matrix representation. As a matter of fact it is so easy to understand that even the biggest idiots on this planet could understand it if they wanted. Of course math professors don’t want to understand 3D numbers so also this new school year nothing will happen on that front…

Did you know that math professors study the periodic system? Yes they do, anyway in my home country the Netherlands they do because every year they get a pay rise and that pay rise is called a periodic. And as such they study the periodic system deep and hard…

I classified this post only under the categories ‘3D complex numbers’ and ‘matrix representations’ and left all stuff related to exponential circles out. Yet the exponential circle stuff is interesting; after reading this post try to find out if the numbers alpha (the midpoint of the exponential circles) are symmetrix (yes). And the two numbers tau (the log of the first imaginary unit on the circular and complex 3D space) are anti-symmetrix (yes).

This post is just over 7 pictures long. As the background picture I used the one I crafted for the general theorem of Pythagoras. (Never read that one? Use the search funtion for this website please!) All pictures are of the usual size namely 550×775 pixels.

It is a cute background picture, I remember it was relatively much work but the result was fine.

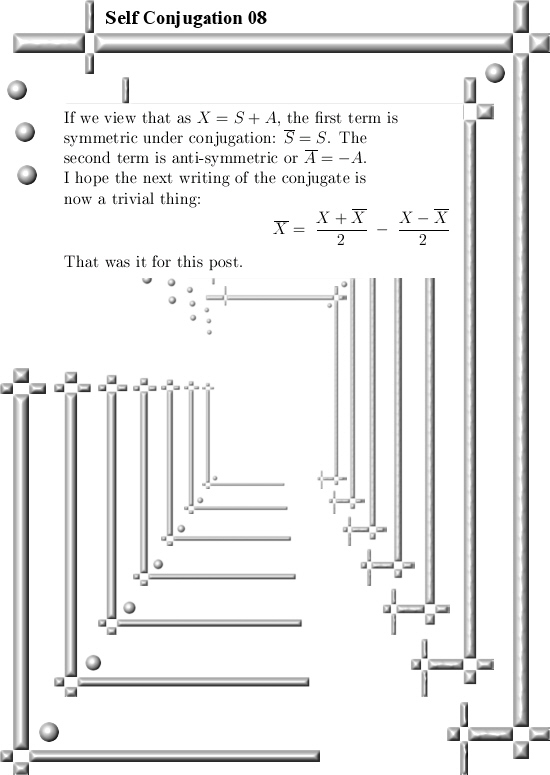
Ok, that was it for this update. Although it is so very simple (for years I did not want to write of just two simple planes that contain all the self-conjugate numbers) but why make it always so difficult? Come on it is summer time and in the summer almost all things are more important than math. For example goalkeeper cat is far more important compared to those stupid 3D numbers. So finally I repost a video about a cat and that makes me very similar to about 3 billion other people.

Till updates & thanks for your attention.

Making a permanent magnet using 20 thousand amps of electric current.

Magnetism

A lovely video was found where a guy from the Nottingham university is showing his workplace around. And they have that heavy equipment for making permanent magnets in just one blast. In the first five years of looking at magnetism I only told you about that slow process of heating up the material till above the Curie temperature, applying an external magnetic field, cool everything down slowly and voila: there are your permanent magnets!
But you can do it in one blast too, all you need is a very strong applied magnetic field. For me that is nothing new because my father worked at the local electricity plant and decades back they too had the equipment to make a permanent magnet in one short blast. At an electricity plant they have plenty of electricity anyway so why waste that?
(My father worked at the electric meter department and in those times they used permanent magnets in the electricity meters you had in your home or your business.)

Anyway, if my version of electron spin is true and electrons are not magnetic dipoles but come in two varieties carrying magnetic charge, in that case the ‘permanent’ in a permanent magnet arises from the fact that the unpaired electrons are shielded in the inner atomic orbitals. That is what makes them permanent… All that blah blah of electron spins aligning themselves to the applied magnetic field is pure nonsense, that blah blah does not explain why the magnetism is permanent.
Of course professional physics professors will always point to the tiny detail that if you think you understand quantum mechancis, you don’t understand quantum mechanics…
Now I too have a lot of things that I do not understand in quantum mechancis, but I think the electron being a magnetic dipole is 100% bullshit. They carry magnetic charge because that makes more sense and is a far more simple explanation of what we observe…

After having said that, if a permanent magnet always has it’s unpaired electrons that give rise to the emergent magnetism always in it’s inner orbitals, in that case if you blast them with a giant external magnetic field they should always heat up. They heat up because the unpaired electrons feels a relatively giant force from the applied magnetic field and as such are ripped out of those inner orbitals. And all ripped out electrons are replaced by electrons of the opposite magnetic charge…
It’s as simple as it is.

Here is the video it is only 15 minutes long:

How do you prove electron bipolar magnetism?

Ok, let me end this post with a picture made from two screen shots from the video. In the top screen shot you see at the left those strips of metal. Wow man, those strips of metal are the wires that transport the 10 to 20 thousand Ampere blast.
In the lower screen shot you see the blue machine where the magic seems to happen.

Ok that was it. If you make permanent magnets and they are not heated at the end, I am wrong about my electron idea’s… Only a professional physics professor will lamentate that applying a short energy burst of only 20 thousand amps will likely heat up everything.

End of this post.

But are these quadratic forms?

3D complex numbers, Exponential circle, Matrix representation

This is a lazy easy going summer post, it does not have much mathematical depth. Let’s say the depth of a bird bath. But with most posts I write you also need a lot of knowledge about what was in previous posts and for the average person coming along that is often too time consuming… So we keep it simple today; quadratic forms on 3D space.

If you have had one or two courses of linear algebra you likely have encountered quadratic forms. They are often denoted as Q(X) where the X is a column matrix and the quadratic form is defined as Q(X) = XT A X. Here XT is the transponent of X so that would be a matrix row. As you might guess, the X column matrix contains the variables while the constant square matrix A is the source of coefficients in the quadratic form Q(X).  In most literature it is told the matrix A is symmetric, of course there is no reason at all for that; any square matrix will do. On the other hand it is easy to see or to show that if a square matrix is anti-symmetric the corresponding quadratic form will always be zero everywhere.

In this post we will take matrices that are always the matrix representation of 3D complex & circular numbers. Matrix representations are a complete category on this website so if you don’t know them you must look that up first. (Oh oh, here I go again: this was supposed to be easy but now the average reader must first try to understand matrix representations of higher dimensional multiplications…)

Compared to the previous update on the likely failure of all fusion reactors this post is far less dramatic. If in the future I am right and we will never have fusion power, that will be the difference between life and death of hundreds of millions of people in the long run… So in order to be a bit less depressing let’s lift the spirits by a lightweight new post on quadratic forms! Why not enjoy life as long as it lasts?

Ok, the actual post is seven pictures long, all in the usual size of 550×775 pixels.













As you see the math is only bird bath deep.

I have to admit that for me the use of the number alpha was important because that is at the center of the exponential circles in the 3D complex and circular spaces. So I have a legitimate reason to post this also under the category ´exponential circle´. And from the non-bird bath deep math, that is the big math ocean that is very deep, I like to classify as much posts under that category ´exponential circles´.

Ok, let´s leave it with that and try to upload this post. Till updates my dear reader.