Category Archives: CR equations

Cauchy-Riemann equations for a ‘golden ratio’ 2D multiplication.

2D multiplications, CR equations

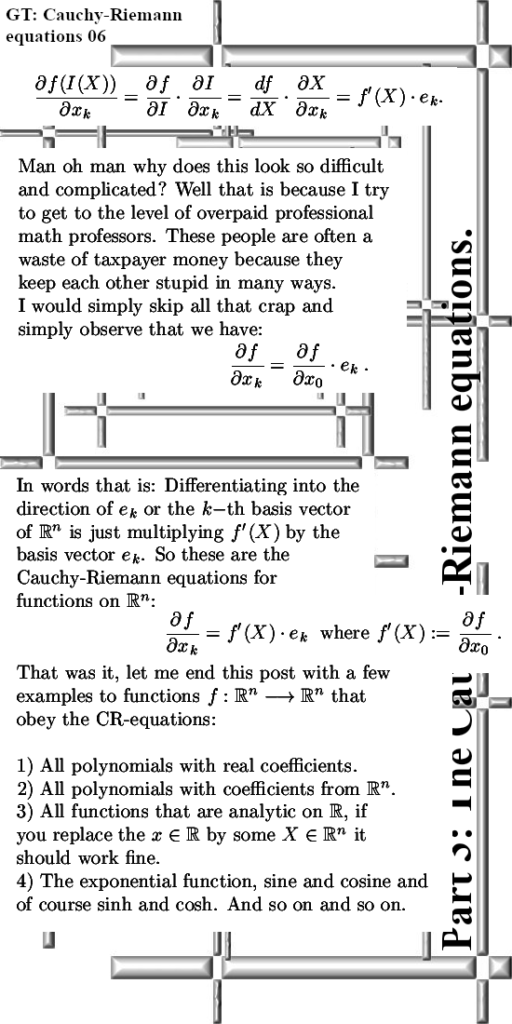
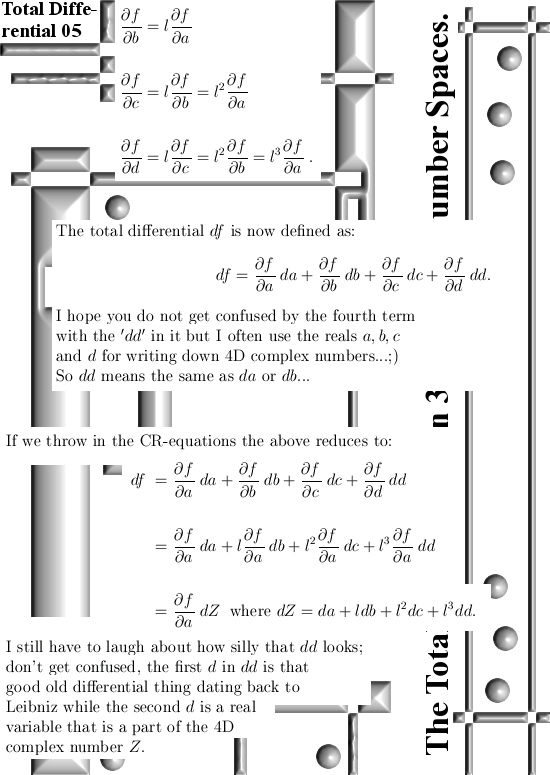
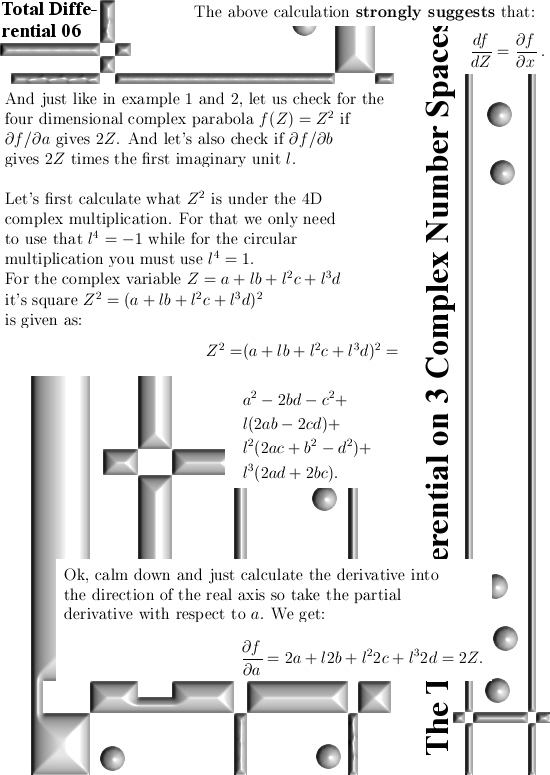
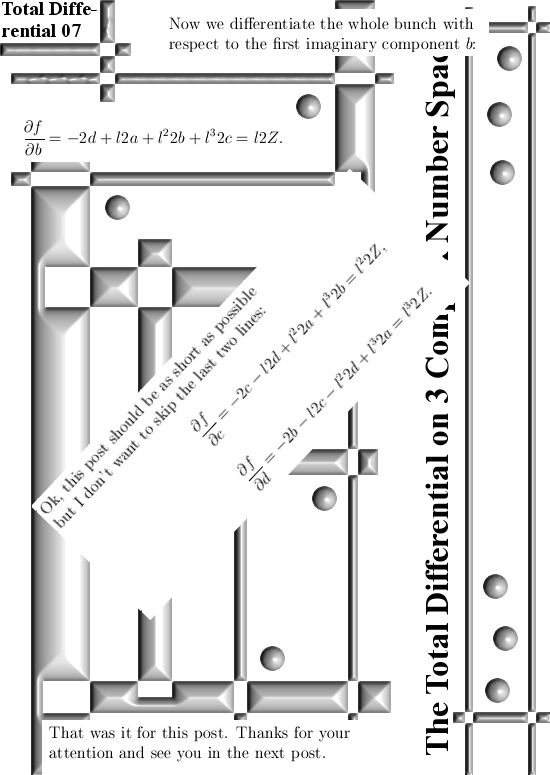
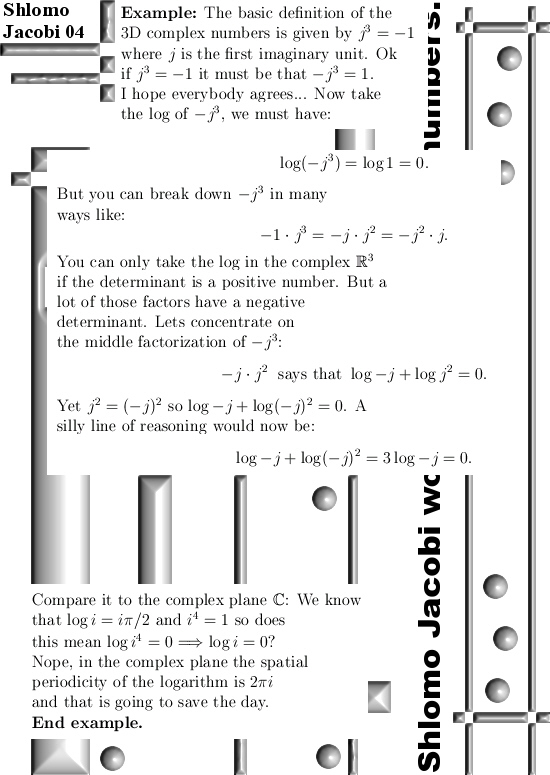
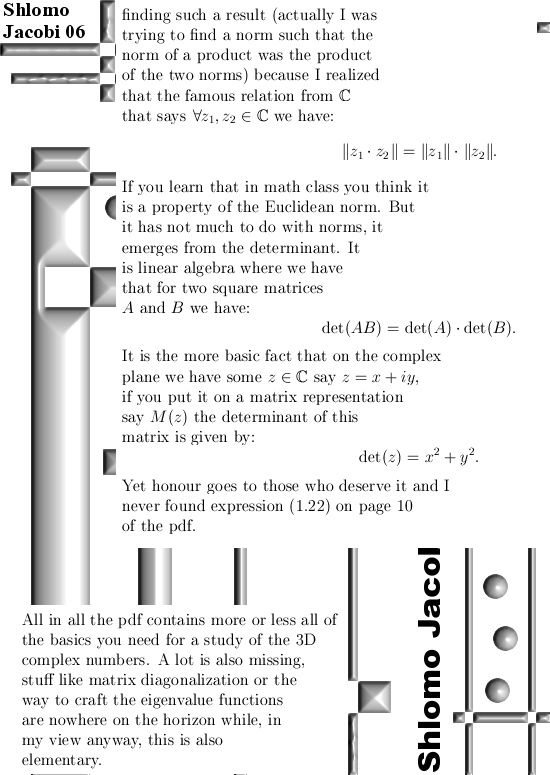
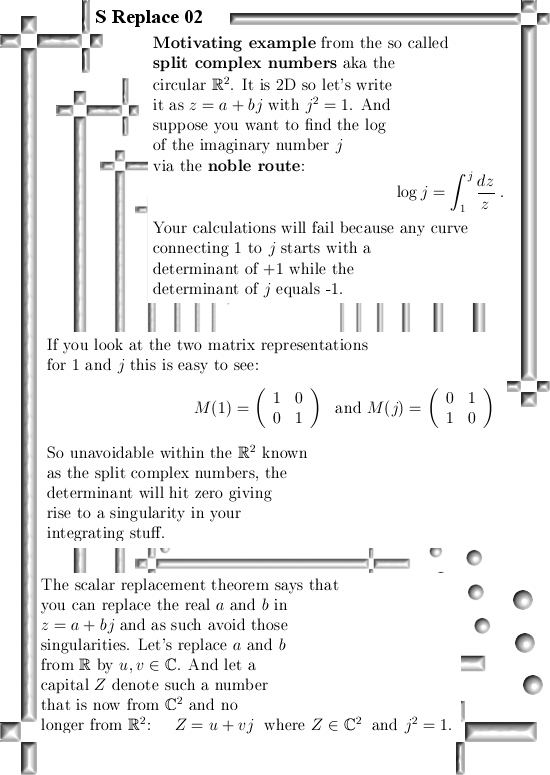
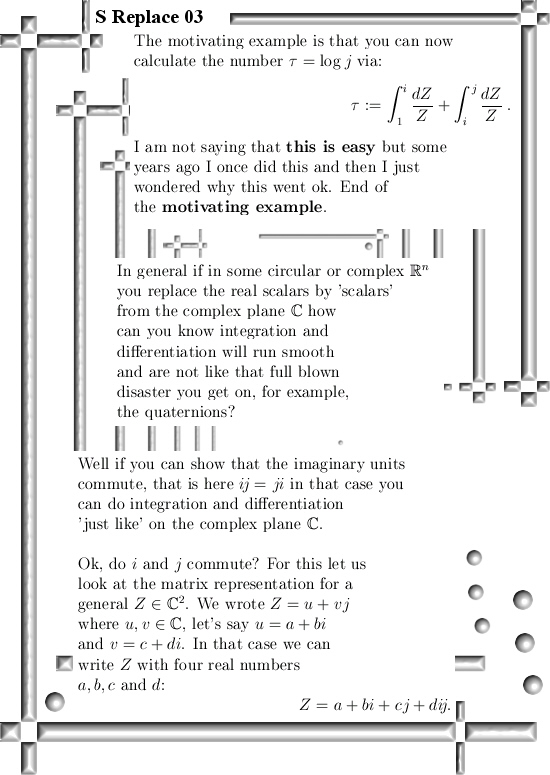
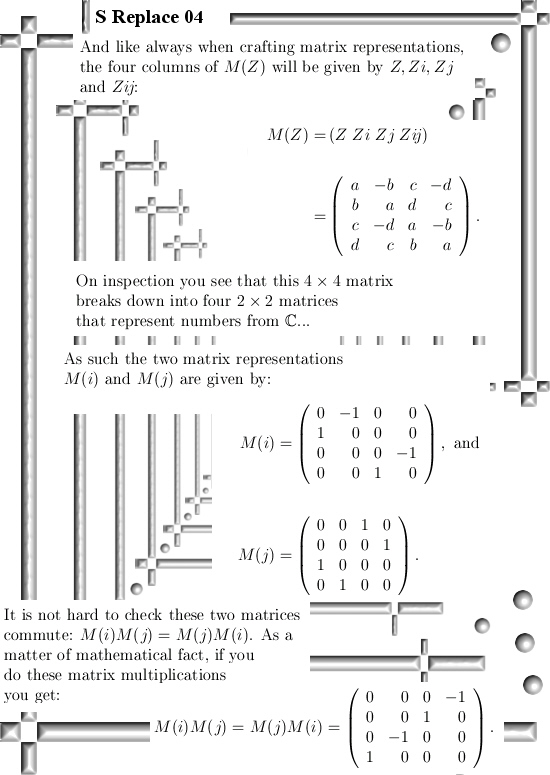
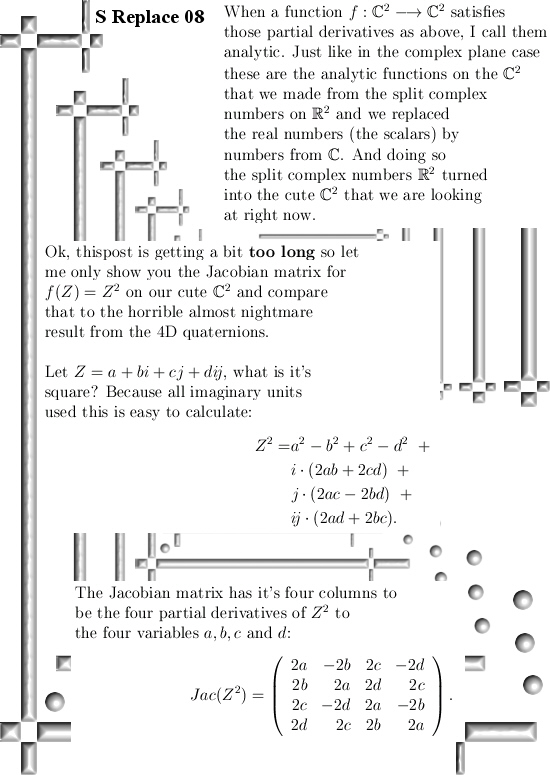
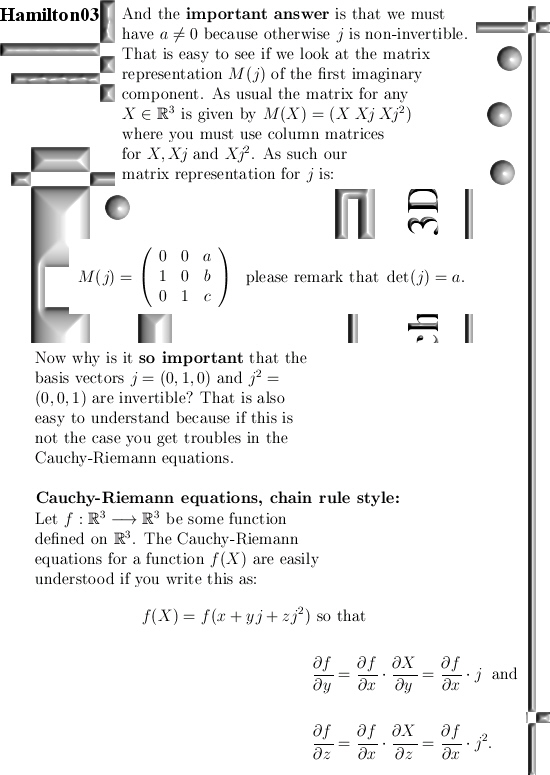
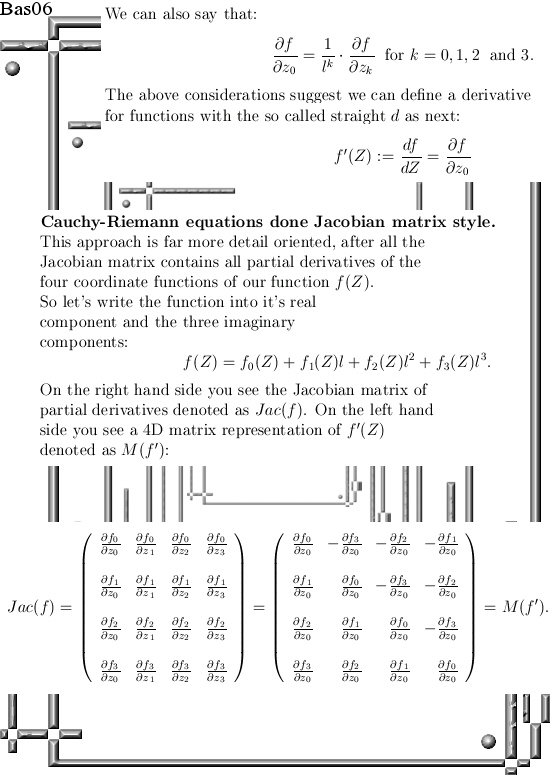
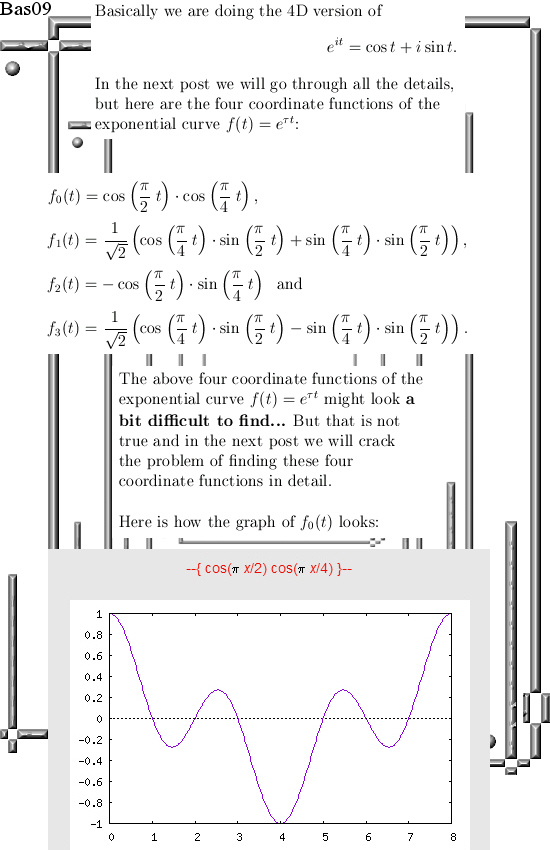
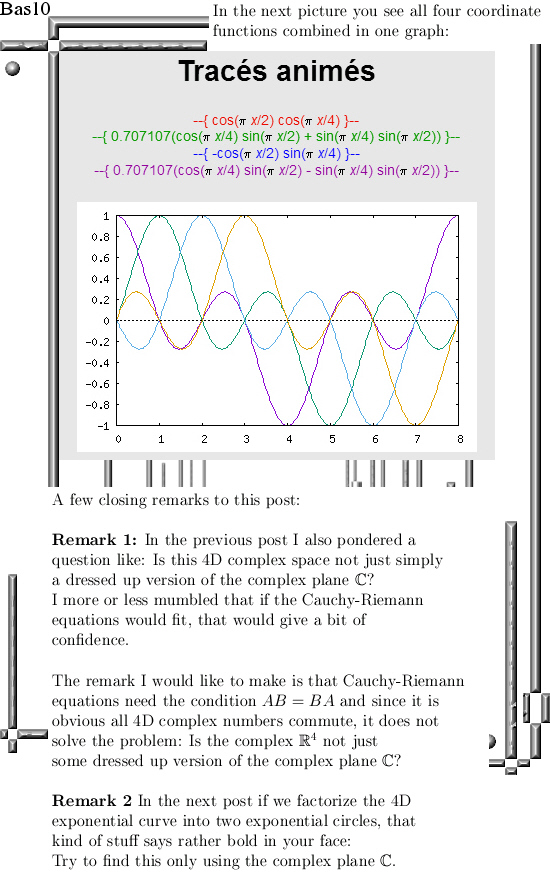
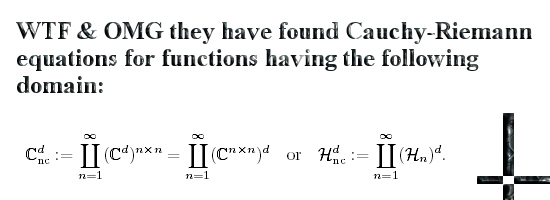Even if you change the multiplication in the plane away from the complex or split complex multiplication it is always easy to find the famous CR-equations. And if you have those in the pocket you can differentiate functions defined on the space you made ‘just like’ on the real line.

After all the CR-equations only need that the numbers commute, you also need to make sure that all basis vectors have an inverse but that are the only restrictions. As far as I know in the math world of the universities the CR-equations are only used in the complex plane, may be some stuff with multiple complex variables and that’s all there is in that part of the math universe.

Originally I wrote the post in just one go and one day later when I read it I was rewarded with a lot of stupid typo’s. Stuff like mindlessly typing x and y where it should have been a and b, also I added the inverse of the imaginary unit because after all I said it was important in the previous post where we looked at CR-equations in the case of a more general n-dimensional space.

An interesting feature of the two dimensional plane is that the two basis vectors 1 and i always commute no matter what you come up with for i^2.
I hope the reader is familiar with the fact that on the complex numbers you have the square of i being minus one and plus one for the split complex numbers. In this post we will look at a 2D multiplication that is ruled by i^2 = 1 + i, so you can view this as a minor modification of the split complex numbers.

At first I named the multiplication a ‘strange multiplication’ but one day later I realized that the age old golden ratio has the same property as my imaginary unit i. If you square the golden ratio, that is also the same as the golden ratio plus one. So I renamed it to the golden ratio multiplication. I know it is a little click baity because the golden ratio itself is not used but only the polynomial equation you need to calculate the golden ratio. Universities have their multi-million marketing budgets, still can’t find 3D complex numbers by the way and I have my free tiny click baity golden ratio multiplication. I think it is an allowed sin.

Did you know that if there is something wrong with a product, it always needs massive marketing budgets. Just look at Coca Cola, without the advertisements the stuff should gradually sell less and less because it is not a healthy product. You can say it is an unhealthy product so there is something wrong with it and as such it needs all that marketing stuff in order to survive.

This post is only four pictures long, I hope it is a bit more easy to digest because it is only two dimensions. So lets go to the math in the four pictures:

Ok, that was it for this post. Thanks for your attention.

General Theory Part 3: Cauchy-Riemann equations.

3D complex numbers, 4D complex numbers, 5D complex numbers, CR equations, Uncategorized

There are many ways to introduce CR-equations for higher dimensional complex and circular numbers. For example you could remark that if you have a function, say f(X), defined on a higher dimensional number space, it’s Jacobian matrix should nicely follow the matrix representation of that particular higher dimensional number space.
I didn’t do that, I tried to formulate in what I name CR-equations chain rule style. A long time ago and I did not remember what text it was but it was an old text from Riemann and it occured he wrote the equations also chain rule style. That was very refreshing to me and it showed also that I am still not 100% crazy…;)
Even if you know nothing or almost nothing about say 3D complex numbers and you only have a bit of math knowledge about the complex plane, the way Riemann wrote it is very easy to understand. Say you have a function f(z) defined on the complex plane and as usual we write z = x + iy for the complex number, likely you know that the derivative f'(z) is found by a partial differentiation to the real variable x. But what happens if you take the partial differential to the variable y?
That is how Rieman formulated it in that old text: you get f'(z) times i. And that is of course just a simple application of the chain rule that you know from the real line. And that is also the way I mostly wrote it because if you express it only in the diverse partial differentials, that is a lot of work in my Latex math typing environment and for you as a reader it is hard to read and understand what is going on. In the case of 3D complex or circular numbers you already have 9 partial differentials that fall apart into three groups of three differentials each.
In this post I tried much more to hang on to how differentiation was orginally formulated, of course I don’t do it in the ways Newton and Leibniz did it with infitesimals and so on but in a good old limit.
And in order to formulate it in limits I constantly need to divide by vectors from higher dimensional real spaces like 3D, 4D or now in the general case n-dimensional numbers. That should serve as an antidote to what a lot of math professors think: You cannot divide by a vector.
Well may be they can’t but I can and I am very satisfied with it. Apperently for the math professors it is too difficult to define multiplications on higher dimensional spaces that do the trick. (Don’t try to do that with say Clifford algebra’s, they are indeed higher dimensional but as always professional math professors turn the stuff into crap and indeed on Clifford algebra’s you can’t divide most of the time.)

May be I should have given more examples or work them out a bit more but the text was already rather long. It is six pictures and picture size is 550×1100 so that is relatively long but I used a somehow larger font so it should read a bit faster.

Of course the most important feature of the CR-equations is that in case a function defined on a higher dimensional space obeys them, you can differentiate just like you do on the real line. Just like we say that on the complex plane the derivative of f(z) = z^2 is given by f'(z) = 2z. Basically all functions that are analytic on the real line can be expanded into arbitrary dimension, for example the sine and cosine funtions live in every dimension. Not that math professors have only an infitesimal amount of interest into stuff like that, but I like it.
Here are the six pictures that compose this post, I hope it is comprihensible enough and more or less typo free:

Ok that was it, thanks for your attention and I hope that in some point in your future life you have some value to this kind of math.

The total differential for the complex plane & the 3D and 4D complex numbers.

3D complex numbers, 4D complex numbers, CR equations

I am rather satisfied with the approach of doing the same stuff on the diverse complex spaces. In this case the 2D complex plane and the 3D & 4D complex number systems. By doing it this way it is right in your face: a lot of stuff from the complex plane can easily be copied to higher dimensional complex numbers. Without doubt if you would ask a professional math professor about 3D or higher dimensional complex numbers likely you get a giant batagalization process to swallow; 3D complex numbers are so far fetched and/or exotic that it falls outside the realm of standard mathematics. “Otherwise we would have used them since centuries and we don’t”. Or words of similar phrasing that dimishes any possible importance.

But I have done the directional derivative, the factorization of the Laplacian with Wirtinger derivatives and now we are going to do the total differential precisely as you should expect from an expansion of the century old complex plane. There is nothing exotic or ‘weird’ about it, the only thing that is weird are the professional math professors. But I have given up upon those people years ago, so why talk about them?

In the day to day practice it is a common convention to use so called straight d‘s to denote differentiation if you have only one variable. Like in a real valued function f(x) on the real line, you can write df/dx for the derivative of such a function. If there are more then one variable the convention is to use those curly d’s to denote it is partial differentiation with respect to a particular variable. So for example on the complex plane the complex variable z = x + iy and as such df/dz is the accepted notation while for differentiation with respect to x and y you are supposed to write it with the curly d notation. This practice is only there when it comes to differentiation, the opposite thing is integration and there only straight d‘s are used. If in the complex plane you are integrating with respect to the real component x you are supposed to use the dx notation and not the curly stuff.
Well I thought I had all of the notation stuff perfectly figured out, oh oh how ultrasmart I was… Am I writing down the stuff for the 4D complex numbers and I came across the odd expression of dd. I hope it does not confuse you, in the 4D complex number system I always write the four dimensional numbers as Z = a + bl + cl^2 + dl^3 (the fourth power of the imaginary unit l must be -1, that is l^4 = -1, because that defines the behavior of the 4D complex numbers) so inside Z there is a real variable denoted as d. I hope this lifts the possible confusion when you read dd…

More on the common convention: In the post on the factorization of the Laplacian with Wirtinger derivatives I said nothing about it. But in case you never heard about the Wirtinger stuff and looked it up in some wiki’s or whatever what, Wirtinger derivatives are often denoted with the curly d‘s so why is that? That is because Wirtinger derivatives are often used in the study of multi-variable complex analysis. And once more that is just standard common convention: only if there is one variable you can use a straight d. If there are more variable you are supposed to write it with the curly version…

At last I want to remark that the post on the factorization of the Laplacian got a bit long: in the end I needed 15 pictures to publish the text and I worried a bit that it was just too long for the attention span of the average human. In the present years there is just so much stuff to follow, for most people it is a strange thing to concentrate on a piece of math for let’s say three hours. But learning new math is not an easy thing: in your brain all kind of new connections need to be formed and beside a few hours of time that also needs sleep to consolidate those new formed connections. Learning math is not a thing of just spending half an hour, often you need days or weeks or even longer.

This post is seven pictures long, have fun reading it and if you get to tired and need a bit of sleep please notice that is only natural: the newly formed connetions in your brain need a good night sleep.

Here we go with the seven pictures:

Yes, that’s it for this post. Sleep well and think well & see you in the next post. (And oh oh oh a professional math professor for the first time in his or her life they calculate the square Z^2 of a four dimensional complex number; how many hours of sleep they need to recover from that expericence?)
See ya in the next post.

Factorization of the Laplacian (for 2D, 3D and 4D complex numbers).

3D complex numbers, 4D complex numbers, CR equations, Laplacian, Magnetism, Quantum mechanics

Originally I wanted to make an oversight of all ways the so called Dirac quantization condition is represented. That is why in the beginning of this post below you can find some stuff on the Dirac equation and the four solutions that come with that equation. Anyway, Paul Dirac once managed to factorize the Laplacian operator, that was needed because the Laplacian is part of the Schrödinger equation that gives the desired wave functions in quantum mechanics. Well I had done that too once upon a time in a long long past and I remembered that the outcome was highly surprising. As a matter of fact I consider this one of the deeper secrets of the higher dimensional complex numbers. Now I use a so called Wirtinger derivative; for example on the space of 3D complex numbers you take the partial derivatives into the x, y and z direction and from those three partial derivatives you make the derivative. And once you have that, if you feed it a function you simply get the derivative of such a function.

Now such a Wirtinger derivative also has a conjugate and the surprising result is that if you multiply such a Wirtinger derivative against it’s conjugate you always get either the Laplacian or in the case of the 3D complex numbers you get the Laplacian multiplied by the famous number alpha.

That is a surprising result because if you multiply an ordinary 3D number X against it’s conjugate you get the equation of a sphere and a cone like thing. But if you do it with parital differential operators you can always rewrite it into pure Laplacians so there the cones and spheres are the same things…

In the past I only had it done on the space of 3D numbers so I checked it for the 4D complex numbers and in about 10 minutes of time I found out it also works on the space of 4D complex numbers. So I started writing this post and since I wanted to build it slowly up from 2D to 4D complex numbers it grew longer than expected. All in all this post is 15 pictures long and given the fact that people at present day do not have those long timespan of attention anymore, may be it is too long. I too have this fault, if you hang out on the preprint archive there is just so much material that often after only five minutes of reading you already go to another article. If the article is lucky, at best it gets saved to my hard disk and if the article has more luck in some future date I will read it again. For example in the year 2015 I saved an article that gave an oversight about the Dirac quantization condition and only now in 2020 I looked at it again…

The structure of this post is utterly simple: On every complex space (2D, 3D and 4D) I just give three examples. The examples are named example 1, 2 and not surprising I hope, example 3. These example are the same, only the underlying space of complex numbers varies. In each example number 1 I define the Wirtinger derivative, in example 2 I take the conjugate while in the third example on each space I multiply these two operators and rewrite the stuff into Laplacians. The reason this post is 15 pictures long lies in the fact that the more dimensions you have in your complex numbers the longer the calculations get. So it goes from rather short in the complex plane (the 2D complex numbers) to rather lengthy in the space of 4D complex numbers.

At last I would like to remark that those four simultanious solutions to the Dirac equation it once more shouts at your face: electrons carry magnetic charge and they are ot magnetic dipoles! All that stuff like the Pauli matrices where Dirac did build his stuff upon is sheer difficult nonsense: the interaction of electron spin with a magnetic field does not go that way. The only reason people in the 21-th century think it has some merits is because it is so complicated and people just loose oversight and do not see that it is bogus shit from the beginning till the end. Just like the math professors that neatly keep themselves stupid by not willing to talk about 3D complex numbers. Well we live in a free world and there are no laws against being stupid I just guess.

Enough of the blah blah blah, below are the 15 pictures. And in case you have never ever heard about a thing known as the Wirtinger derivative, try to understand it and may be come back in five or ten years so you can learn a bit more…
As usual all pictures are 550×775 pixels in size.

Oh oh the human mind and learning new things. If a human brain learns new things like Cauchy-Riemann equations or the above factoriztion of the Laplacian, a lot of chages happen in the brain tissue. And it makes you tired and you need to sleep…
And when you wake up, a lot of people look at their phone and may be it says: Wanna see those new pictures of Miley Cyrus showing her titties? And all your new learned things turn into insignificance because in the morning what is more important compared to Miley her titties?

Ok my dear reader, you are at the end of this post. See you in the next post.

The directional derivative (for 3D & 4D complex numbers).

3D complex numbers, 4D complex numbers, CR equations, Matrix representation

A couple of days ago all of a sudden while riding my bicycle I calculated what the so called directional derivative is for 3D & 4D complex numbers. And it is a cute calculation but I decided not to write a post about it. After all rather likely I had done stuff like that many years ago.

Anyway a day later I came across a few Youtube video’s about the directional derivative and all those two guys came up with was an inner product of the gradient and a vector. Ok ok that is not wrong or so, but that is only the case for scalar valued functions on say 3D space. A scalar field as physics people would say it. The first video was from the Kahn academy and the guy from 3Blue1Brown has been working over there lately. It is amazing that just one guy can lift such a channel up in a significant manner. The second video was from some professional math professor who went on talking a full 2.5 hour about the directional derivative of just a scalar field. I could not stand it; how can you talk so long about something that is so easy to explain? Now I do not blame that math professor, may be he was working in the USA and had to teach first year math students. Now in the USA fresh students are horrible at math because in the USA the education before the universities is relatively retarded.

Furthermore I tried to remember when I should have done the directional derivative. I could not remember it and in order to get rid of my annoyance I decided to write a small post about it. Within two hours I was finished resulting in four pictures of the usual 550×775 pixel size. So when I work hard I can produce say 3 to 4 pictures in two hours of time. I did not know that because most of the time I do not work that fast or hard. After all this is supposed to be a hobby so most of my writing is done in a relaxed way without any hurry. I have to say that may be I should have taken a bit more time at the end where the so called Cauchy-Riemann equations come into play. I only gave the example for the identiy function and after that jumped to the case of a general function. May be for the majority of professional math professors that is way to fast, but hey just the simple 3D complex numbers are ‘way to fast’ for those turtles in the last two centuries…

Anyway, here is the short post of only 4 pictures:

Should I have made the explanation longer? After all so often during the last years I have explained that the usual derivative f'(X) is found by differentiating into the direction of the real numbers. At some point in time I have the right to stop explaining that 1 + 1 = 2.

Also I found a better video from the Kahn academy that starts with a formal definition of the directional derivative:

At last let me remark that this stuff easily works for vector valued functions because in the above limit you only have to subtract two vectors and that is always allowed in any vector space. And only if you hang in a suitable multiplication like the complex multiplication of 3D or 4D real space you can tweak it like in the form of picture number 4 above.

That was all I had for you today, this is post number 166 already so I am wondering if this website is may be becoming too big? If people find something, can they find what they are searching for or do they get lost in the woods? So see you in another post, take care of yourself & till the next post.

On the work of Shlomo Jacobi & a cute more or less new Euler identity.

3D complex numbers, CR equations, Exponential circle, Matrix representation

For a couple of years I have a few pdf files in my possession written by other people about the subject of higher dimensional complex and circular numbers. In the post we will take a look at the work of Shlomo Jacobi, the pdf is not written by him because Shlomo passed away before it was finished. It is about the 3D complex numbers so it is about the main subject of this website.

Let me start with a link to the preprint archive:

On a novel 3D hypercomplex number system

Link used: http://search.arxiv.org:8081/paper.jsp?r=1509.01459&qid=1603841443251ler_nCnN_1477984027&qs=Shlomo+Jacobi&in=math

Weirdly enough if you search for ‘3D hypercomplex number’ the above pdf does not pop up at all at the preprint archive. But via his name (Shlomo Jacobi) I could find it back. Over the years I have found three other people who have written about complex numbers beyond the 2D complex plane. I consider the work of Mr. Jacobi to be the best so I start with that one. So now we are with four; four people who have looked at stuff like 3D complex numbers. One thing is directly curious: None of them is a math professional, not even a high school teacher or something like that. I think that when you are a professional math professor and you start investigating higher dimensional complex numbers; you colleagues will laugh about it because ‘they do not exist’. And in that manner it are the universities themselves that ensure they are stupid and they stay stupid. There are some theorems out there that say a 3D complex field is not possible. That is easy to check, but the math professionals make the mistake that they think 3D complex numbers are not possible. But no, the 2-4-8 theorem of say Hurwitz say only a field is not possible or it says the extension of 2D to 3D is not possible. That’s all true but it never says 3D complex numbers are not possible…

Because Shlomo Jacobi passed away an unknown part of the pdf is written by someone else. So for me it is impossible to estimate what was found by Shlomo but is left out of the pdf. For example Shlomo did find the Cauchy-Riemann equations for the 3D complex numbers but it is only in an epilogue at the end of the pdf.

The content of the pdf can be used for a basic introduction into the 3D complex numbers. It’s content is more or less the ‘algebra approach’ to 3D complex numbers while I directly and instantly went into the ‘analysis approach’ bcause I do not like algebra that much. The pdf contains all the basic stuff: definition of a 3D complex number, the inverse, the matrix representation and stuff he names ‘invariant spaces’. Invariant spaces are the two sets of 3D complex numbers that make up all the non-invertible numbers. Mr. Jacobi understands the concept of divisors of zero (a typical algebra thing that I do like) and he correctly indentifies them in his system of ‘novel hypercomplex numbers’. There is a rudimentary approach towards analysis found in the pdf; Mr. Jacobi defines three power series named sin1, sin2 and sin3 . I remember I looked into stuff like that myself and somewhere on this website it must be filed under ‘curves of grace’.

A detail that is a bit strange is the next: Mr. Jacobi found the exponential circle too. He litarally names it ‘exponential circle’ just like I do. And circles always have a center, they have a midpoint and guess how he names that center? It is the number alpha…

Because Mr. Jacobi found the exponential circle I applaud him long and hard and because he named it’s center the number alpha, at the end I included a more or less new Euler identity based on a very simple property of the important number alpha: If you square alpha it does not change. Just like the square of 1 is 1 and the square of 0 is 0. Actually ‘new’ identity is about five years old, but in the science of math that is a fresh result.

The content of this post is seven pictures long, please read the pdf first and I hope that the mathematical parts of your brain have fun digesting it all. Most pictures are of the standard size of 550×775 pixels.

Yes all you need is that alpha is it’s own square.

Ok ok, may be you need to turn this into exponential circles first in order to craft the proof that a human brain could understand. And I am rolling from laughter from one side of the room to the other side; how likely is it that professional math professors will find just one exponential circle let alone higher dimensional curves?

I have to laugh hard; that is a very unlikely thing.

End of this post, see you around & see if I can get the above stuff online.

The scalar replacement theorem.

CR equations, Matrix representation

Ok ok I was a bit lazy but it is finished now so let’s finally post this scalar replacement theorem. Never in this post I formulate or proof this scalar replacement theorem, but basically this theorem says that if you replace the real numbers (scalars) in the way you describe say 2D split complex numbers by numbers from the complex plane, the result is a space who’s numbers also commute and it even has viable Cauchy Riemann equations. In this post I will write z = x + yj for the 2D circular numbers (also known as the split complex numbers) and write z = x + yi for numbers from the complex plane. If you combine such spaces it must have imaginary units that are different in notation, so j is the imaginary unit that does j^2 = 1 while the good ol i from the complex plane is known for it’s important property that i^2 = -1.

If we replace the x and y in z = x + yj by complex numbers we get a new 4D space where both j and i place there role. All in all those 4D numbers will be written as Z = a + bi + cj + dij. Of course the a, b, c and d are real numbers and as such this new space is 4D.

A long time ago I once used this to calculate the logatithm of j, it worked perfectly and that is why I more or less gave idea’s like that the name of ‘scalar replacement’. Later I found that way of using diagonalization of the matrix representations in order to calculate the logarithm, that is a far more general useable way of calculating logarithms but anyway the original calculation for log j was so cute, I could not abondon it and say to that calculation: From now on you are a poor orphan and no one will help you survive from day to day… How could I abandon such a calculation, better loose the UK a 100 times on a row than abandoning such nice calculations… 😉

But let’s go back to being a serious and responsible adult; the post is relatively long with 10 pictures. As usual I had to leave a lot out and I hope it is more or less easily readable. After all a lot of math out there looks like it is written by people who eat a plate of coal for breakfast. And if you eat coal for breakfast, likely this has an influence on the math you will produce on a particular day… Ok, here we go:

Ok, the goal of this post is of course to make you think a little bit about this 4D space and compare it to the quaternions and stuff. But last year on 2 March I posted the diagonalization method for finding the logarithm of an arbitrary split complex number. Below is a link.

The logarithm of all 2D circular numbers (the split complex numbers).

Let me end this post with a funny mathematical joke about how to NOT WRITE MATH. Using a fucking lot of indices is not a way to make your work readable, here is a picture of what I view as some kind of mathematical joke.

In case you desire a serious headache, go read that file.

https://arxiv.org/pdf/1906.09014.pdf

Ok, end of this post.

Using the Cayley-Hamilton theorem to find ‘all’ multiplications in 3D space.

3D complex numbers, CR equations, Matrix representation, Uncategorized

It is a bit vague what exactly a multiplication is, but I always use things that ‘rotate over the dimensions’. For example on the 3D complex space the imiginary unit is written as j and the powers of j simply rotate over the dimensions because:

j = (0, 1, 0)
j^2 = (0, 0, 1) and
j^3 = (-1, 0, 0). Etc, the period becomes 6 in this way because after the sixth power everything repeats.

In this post we will look at a more general formulation of what the third power of j is. The Cayley-Hamilton theorem says that you can write the third power of 3 by 3 matrices always as some linear combination of the lower powers.

That is what we do in this post; we take a look at j^3 = a + bj + cj^2. Here the a, b and c are real numbers. The allowed values that j^3 can take is what I call the ‘parameter space’. This parameter space is rather big, it is almost 3D real space but if you want the 3D Cauchy-Riemann equations to fly it has to be that a is always non zero. There is nothing mysterious about that demand of being non zero: if the constant a = 0, the imaginary unit is no longer invertible and that is the root cause of a whole lot of trouble and we want to avoid that.

It is well known that sir Hamilton tried to find the 3D complex numbers for about a full decade. Because he wanted this 3D complex number space as some extension of the complex plane, he failed in this detail and instead found the quaternions… But if the 3D numbers were some extension of the 2D complex plane, there should be at least one number X in 3D such that it squares to minus one. At the end I give a simple proof why the equation X^2 = -1 cannot be solved in 3D space for all allowed parameters. So although we have a 3D ocean of parameters and as such an infinite amount of different multiplications, none of them contains a number that squares to minus one…

I gave a small theorem covering the impossibility of solving X^2 = -1 a relative harsh name: Trashing the Hamilton approach for 3D complex numbers. This should not be viewed as some emotional statement about the Hamilton guy. It is just what it says: trashing that kind of approach…

This post is 7 pictures long, each of the usual size of 550×775 pixels.

Test picture, does jpg upload again?












Sorry for the test picture, but the seven jpg pictures refused to upload. And that is strange because they are just seven clean jpg’s. Now it is repaired although I do not understand this strange error.

Anyway have a cool summer. Till updates.

Part 8 of the 4D basics: Wirtinger derivatives.

4D complex numbers, CR equations, Laplacian

This is the 91-th post on this website so surely but slowly this website is growing on. This post was more or less written just for myself; I don’t know if the concept of Wirtinger derivates is used a lot in standard complex analysis but I sure like it so that’s why we take a look at it.

The idea of a Wirtinger derivative is very simple to understand: You have some function f(Z) and by differentiating it in the direction of all four basis vectors you craft the derivative f'(Z) from that.

At the basis for all the calculations we do in this post are the Cauchy-Riemann equations that allow you to rewrite the partial derivatives we put into the Wirtinger derivative.

The main result in this post is as follows:
We take our Wirtinger operator W and we multiply it with the 4D complex conjugate of W and we show that this is a real multiple of the Laplacian.

The 4D case is more or less the same as on the complex plane, that is not a miracle because in previous 4D basics we already observed two planes inside the 4D complex numbers that are isomorphic to the complex plane. So it is not much of a surprise the entire 4D space of complex numbers behaves in that way too; all functions are harmonic that is the Laplacian of such a function is zero.

This post is ten pictures long, most of them are size 550 x 775 but a few of them are a bit broader like 600 x 775 because the calculations are rather wide.

On the scale of things this post is not ultra important or so, it is more like I wrote it for myself and I wanted to look in how much this all was different from the three dimensional case.

Here are the pics:

Further reading from a wiki (of course that is only about 2D complex numbers from the complex plane):
Wirtinger derivatives
https://en.wikipedia.org/wiki/Wirtinger_derivatives

Ok, that was it. Till updates.

The basics of 4D complex numbers.

4D complex numbers, CR equations, Exponential curves, Matrix representation

In the previous post on 4D complex numbers I went a little bit philosophical with asking if these form of crafting a 4D number system is not some advanced way of fooling yourself because your new 4D thing is just a complex plane in disguise…

And I said let’s first craft the Cauchy-Riemann equations for the 4D complex numbers, that might bring a little bit more courage and making us a little bit less hesitant against accepting the 4D complex numbers.

In this post we also do the CR equations and indeed they say that for functions like f(Z) = Z^2 you can find a derivative f'(Z) = 2Z. So from the viewpoint of differentiation and integration we are in a far better spot compared to the four dimensional quaternions from Hamilton. But the fact that the CR equations can be crafted is because the 4D complex numbers commute, that is XY = YX. And on the quaternions you cannot differentiate properly because they do not commute.

So crafting Cauchy-Riemann equations can be done, but it does not solve the problem of may be you are fooling yourself in a complicated manner. Therefore I also included the four coordinate functions of the exponential 4D curve that we looked at in the previous post.

All math loving folks are invited to find the four coordinate functions for themselves, in the next post we will go through all details. And once you understand the details that say the 4D exponential curve is just a product of two exponential circles as found inside our 4D complex numbers, that will convince you much much more about the existence of our freshly unearthed 4D complex numbers.

Of course the mathematical community will do once more in what they are best: ignore all things Reinko Venema related, look the other way, ask for more funding and so on and so on. In my life and life experiences not one university person has ever made a positive difference, all those people are only occupied with how important they are and that’s it. Being mathematical creative is not very high on the list of priorities over there, only conform to a relatively low standard of ‘common talk’ is acceptable behavior…

After having said that, this post is partitioned into five parts and is 10 pictures long. It is relatively basic and in case that for example you have never looked at matrix representations of complex numbers of any dimension, please give it a good thought.

Because in my file I also encountered a few of those professional math professors that were rather surprised by just how a 3 by 3 matrix looks for 3D complex numbers. How can you find that they asked, but it is fucking elementary linear algebra and sometimes I think these people do not understand what is in their own curriculum…

Ok, here are the 10 pictures covering the basic details of 4D complex numbers:

 

 

 

 

 

 

 

 

Ok, that was the math for this post.

And may be I am coming a bit too hard on the professional math professors. After all they must give lectures, they must attend meetings where all kinds of important stuff has to be discussed until everybody is exhausted, they must be available for students with the questions and problems they have, they must do this and must do that.

At the end of the day, or at the end of the working week, how much hours could they do in free thinking? Not that much I just guess…

Let’s leave it with that, see you in the next post.