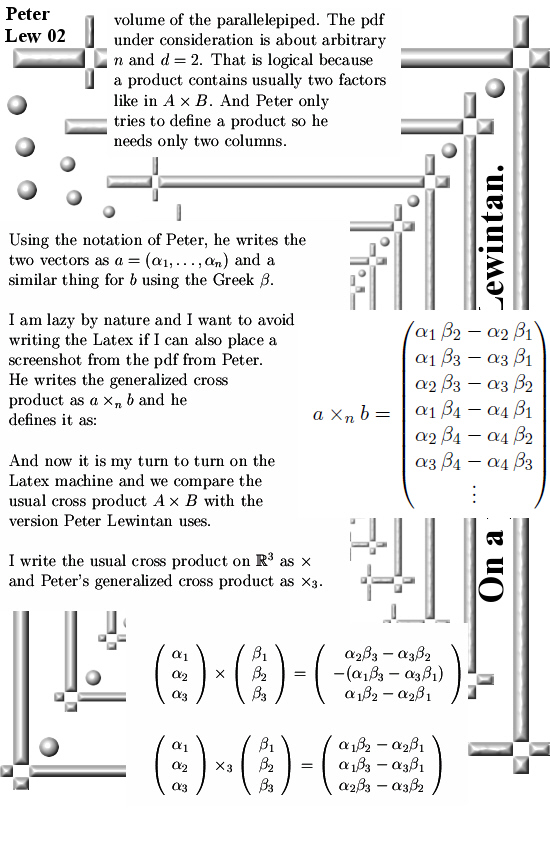
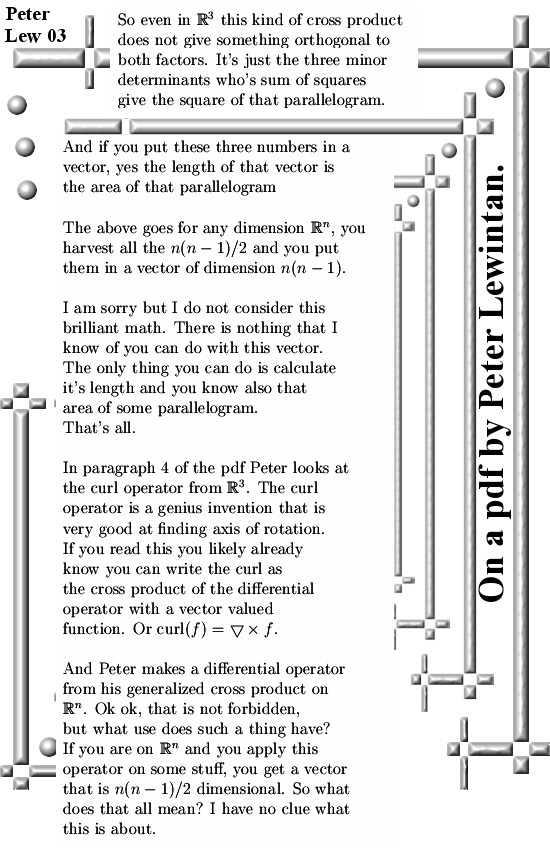
This is one of those videos based in large part on that old theorem of Frobenius that says there are no 3D fields containing the complex numbers from the complex plane. There is another similar proof out, also rather old, that says the same.
Well there is nothing new about that, after all there is nothing in the 3D complex numbers that squares up to -1. (See a few posts back when I wrote the first so called general theory where I show that in all odd-dimensional number systems you cannot solve for X^2 = -1).
It is also not much of a secret that beside 0 there are much more non-invertible numbers in 3D real space. So no, it is not a field but I knew that for over 30 years my dear reader.
Over the years I have joked at many occasions that the only thing math professors are good at is at saying “We cannot find the 3D complex numbers”. And that is so deep ingrained for some strange reason that actually they can’t. Ok ok there is also the question of competence into doing new math research. As a matter of fact most math professors are relatively bad at doing researh on new math stuff. Math professors are rather good at reproducing the good math from the past, in such a comparison they are much more like a classical orchestra that plays old works of music from Bach or any other long dead composer. But most professional musicians do not compose very music for themselves, it is their job to repeat the old music from the past and that’s it. Math professors are just like that often, now that is not only negative or so. For example the proof of the prime number theorem (how much primes are there asymptotically under a given magnitude?) was hard to find and it is long. If you can repeat that proof in front of a class, that is for sure a highly cognitive thing to do. I am not saying all math professors are dumb.
But as far as I know it most of them have a strong tendency for shallow thought, better fast than accurate and much slower. For example in 30 years of time every now and then some folks discover the 3D complex numbers again and oh oh what exiting it is to find the conjugate! They do it all wrong, yes one 100% take the wrong kind of conjugate and after that all calculations fade into total nonsense and as such they too conclude there is not much going on with 3D complex numbers. I have never seen anyone finding the 3D complex exponential, that is what I mean with shallow thinking. People just project on the new stuff things they know from the old stuff and the new stuff ‘must’ for some strange reason obey the old stuff and when that does not happen they begin to cry like the crybabies they are.
I did that too on a few occasions but after doing stupid twice I understood what I was doing wrong: I just was not open minded about how the new stuff actually worked.
Now when I viewed the video for the first time a few weeks back I was relatively annoyed, not only because of the dumb content but also because of the title (3D complex numbers do not exist). But the days after when this new post came to my mind I just felt so tired. Why is it always so fucking stupid and shallow? Why is that year in year out why are all those math professors never evolving, why is it always fucking stupid and no oversight at all?
So I did not have a good feeling about it and because the video is so stupid I could easily write 20 different posts and that made me feel even more tired and exhausted because these people just don’t improve.
Anyway I decided to keep it short and simple and only point out that the two most important new numbers in the 3D complex numbers are the number tau and alpha that are related to the 3D complex exponential. These two numbers if you multiply them that gives zero, the property that non-zero numbers can multiply to zero is called divisors of zero.
And guess what, the video from Michael Penn begins with a small list of the properties that 3D numbers have to obey in case you will have something meaningful or so as Michael says it. Well in his small list is indeed it must be a field and also it does not have divisors of zero. Furthermore Michael did not figure it out himself but uses the work of another person so we have everything combined: Shallow thinking combined with repeating the work of other people.
Here is the video:
Left is placing the two pictures that compose this post here below. And I have an extra pdf with that Frobenius stuff in it, it is hard to read and is precisely the kind of math I avoid to write down. You can find the Forbenius classification from page 26 of the pdf.


The pdf from Ray E. Artz:
For myself speaking: I consider this pdf a disaster to read. It is all overly complicated formulated with not much math content to it. But it contains a bit of the old school Frobenius stuff so it has some value although it has weird notation that is hard to grasp…
Over time I have come to understand that the 3D complex numbers are an expansion from the real line just like the complex plane is. For example: multiplication in the 3D complex numbers is ruled by the imaginary unit j who’s third power equals minus one: j^3 = -1.
But if you have seen only the complex plane your entire life, in that case you are likely tempted to try and think of it as e to some imaginary power like on the complex plane. But you cannot do that because the number i from the complex plane does not live inside the 3D complex numbers. So for me they have equal right to exist or to study, they are very different but at least you can do complex analysis on the 3D complex numbers and you can’t do that on the famous quaternions.
Now I don’t want to sound as a sour old man, after all this post was not very funny to write but on the scale of things it is just a luxery problem. Let me end this post with thanking you for your attention.