When reading some old texts I found that in the past I named this theorem the Scalar Replacement Theorem and that is may be a better description of the stuff involved. The Sledge Hammer theorem says that if you have say a 3D complex or circular number, you can always replace the reals by numbers from other higher dimensional system.
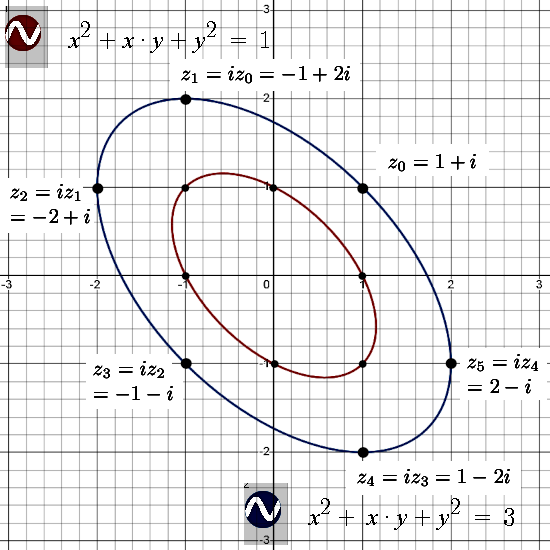
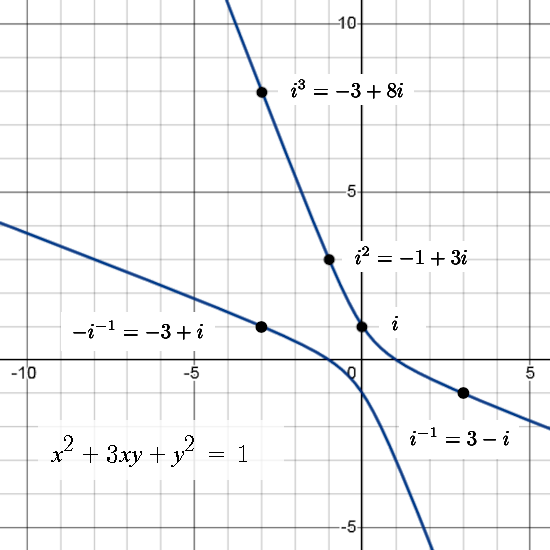
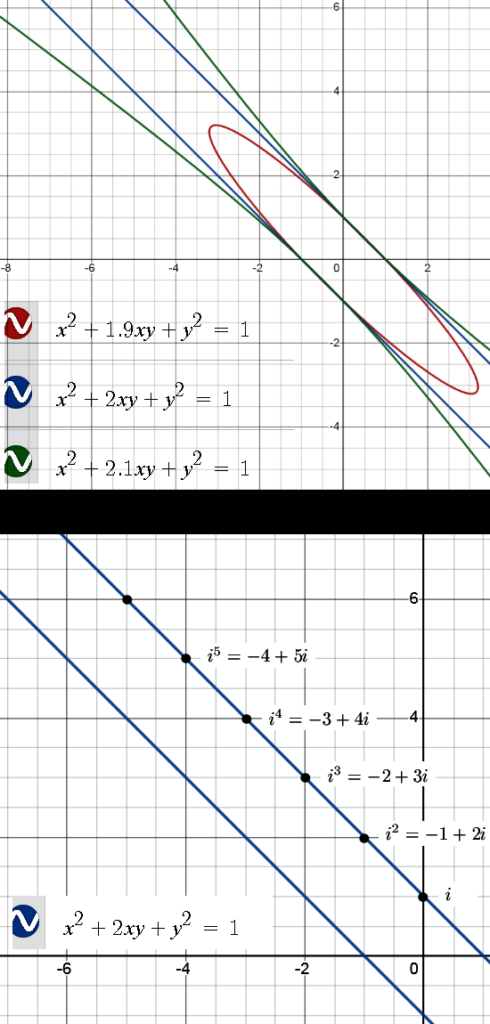
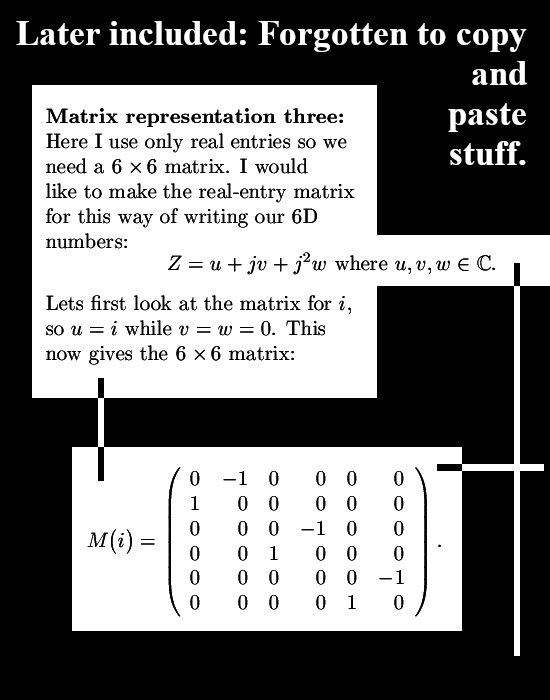
I took the 3D circular numbers, so the third power of the first imaginary unit equals one, and replaced the real x, y and z by the 2D complex numbers from the complex plane. Of course you know that in the complex plane the imaginary unit i squares to minus one so if we replace the reals by 2D complex numbers we get a 6D number system.
The Sledgehammer Theorem says that if you do that, the newly formed 6D number system commutes and if you want you can find the Cauchy-Riemann equations that belong to this particular set of higher dimensional numbers. This is the very first hybrid number system I crafted, it is hybrid because it is not circular nor complex but has imaginary units that are different in that detail.
The main goal of this post is to show that both imaginary units commute and that makes the whole 6D number system commute. I concentrated on two different ways of making a matrix representation and I kept it that way. So the simple to understand thing that ij = ji is the main goal of my new post but from experience I know that for other people it is always amazingly hard to find a conjugate. On the complex plane it is just a flip in the real axis and for some strange reason people always do that and end up with rubbish in say spaces like the 3D circular numbers. Therefore I took the freedom to include the conjugate and of course if you have the conjugate why not try to extract a bit of cute math like the sphere-cone equation from it and see how this looks in this 6D hybrid number system.
The post is seven pictures long and one appendix so all in all eight pictures of size 550×1500 pixels. I tried to keep it all as simple as possible but hey it’s a 6D space made from a 3D circular space and a 2D complex space.
Have fun reading it.







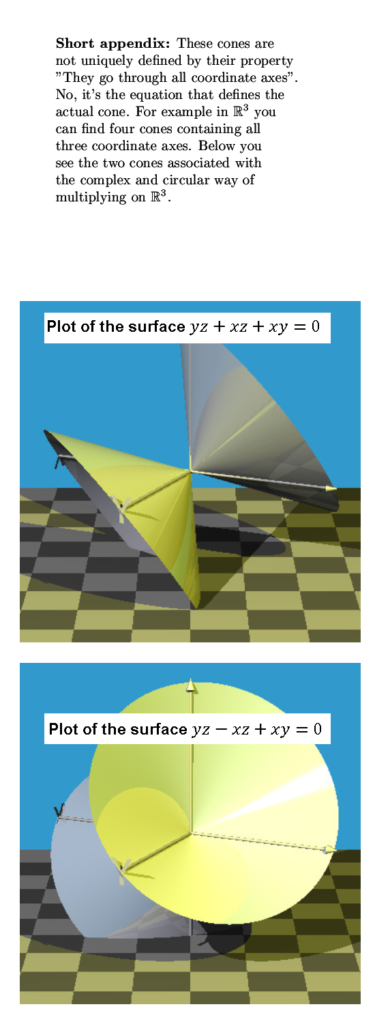
And I made a tiny appendix upon those cone like structures. Only in 3D it is a proper 2D cone of course. It is only to show that a cone is defined by it’s equation and it has the property it goes through all coordinate axes. Even in 3D space there are four cones that include all coordinate axes, I show you the cone associated with the complex and circular 3D spaces.
That was it for this post that despite it’s rather limited math content grew a bit long after all. In case you haven’t fallen asleep right now may I thank you for your attention. May be we do a good old post on magnetism as the next post or just somehting else. I don’t know yet so we’ll see.