Monthly Archives: February 2016

Atomic orbitals, the Schrödinger wave equation and 3D complex numbers.

3D complex numbers, Exponential circle, Laplacian, Quantum mechanics

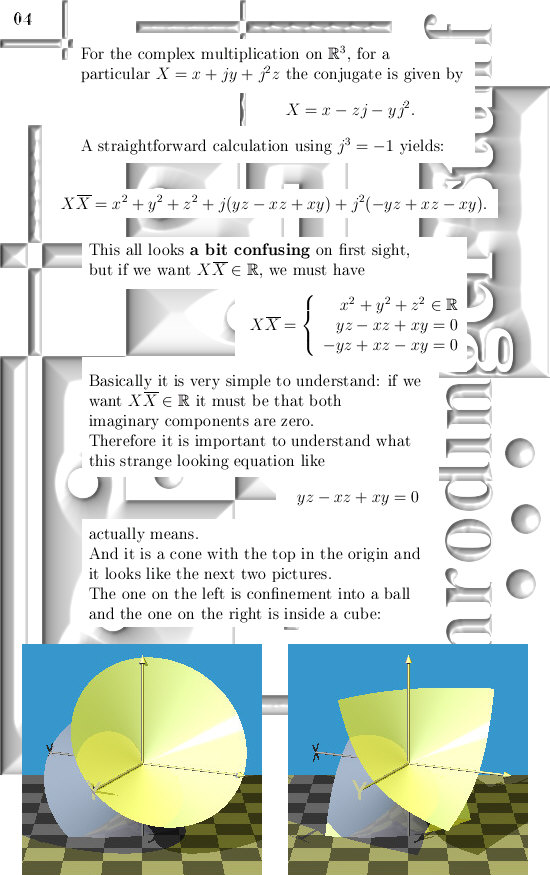
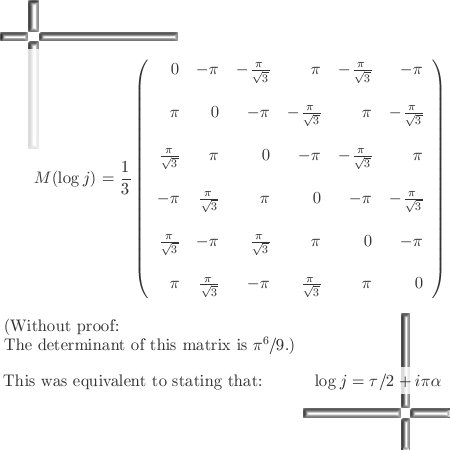
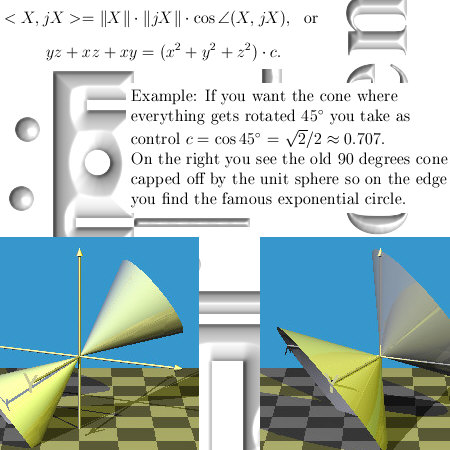
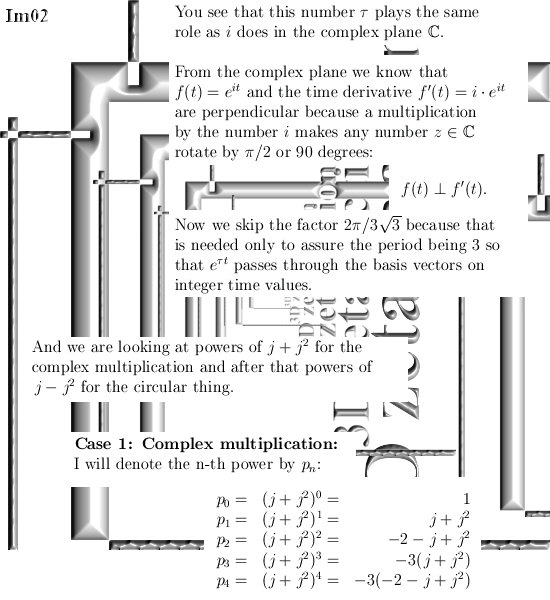
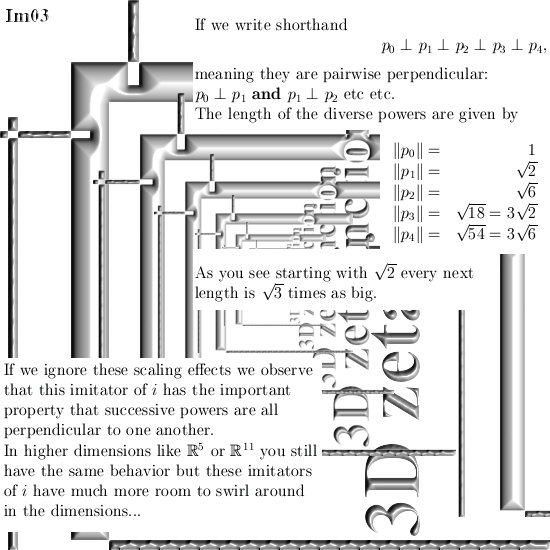
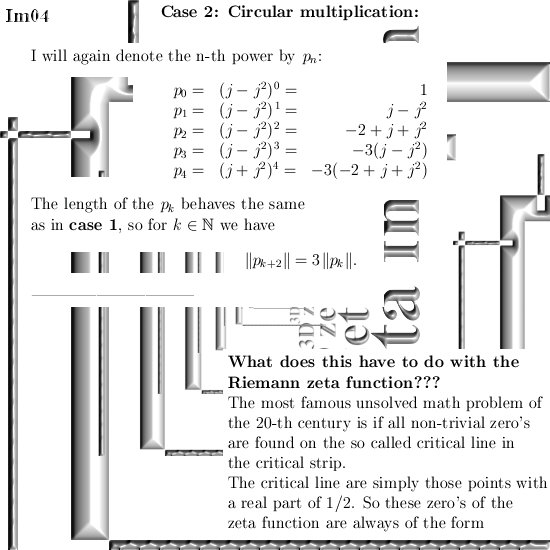
The numerical use of three dimensional complex numbers is almost the same as the situation on the complex plane. This is caused by the simple fact that only on the main cone that includes the three coordinate axes, we have that if you multiply a number X by it’s conjugate, the result is a real number.

In the complex plane this is valid for all numbers in the plane but in higher dimensional complex number systems the situation is different; you must always pick numbers from that main cone where also the exponential circle lives (in 3D) or exponential curves (in higher dimensions).

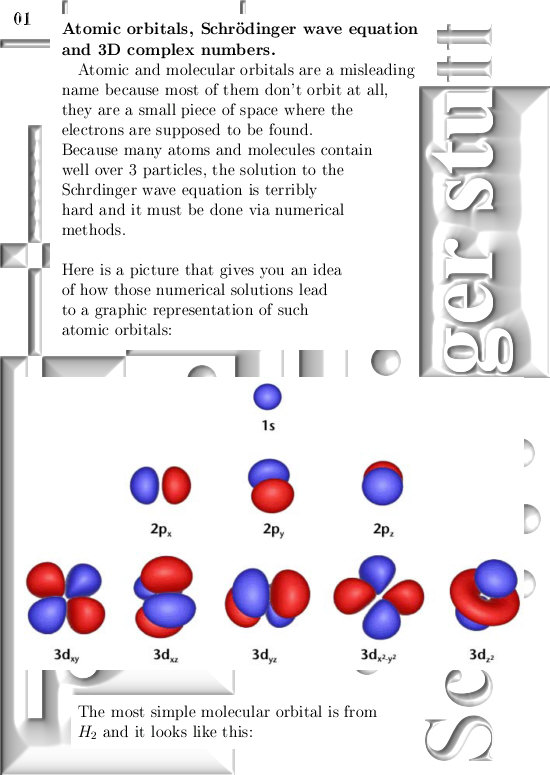
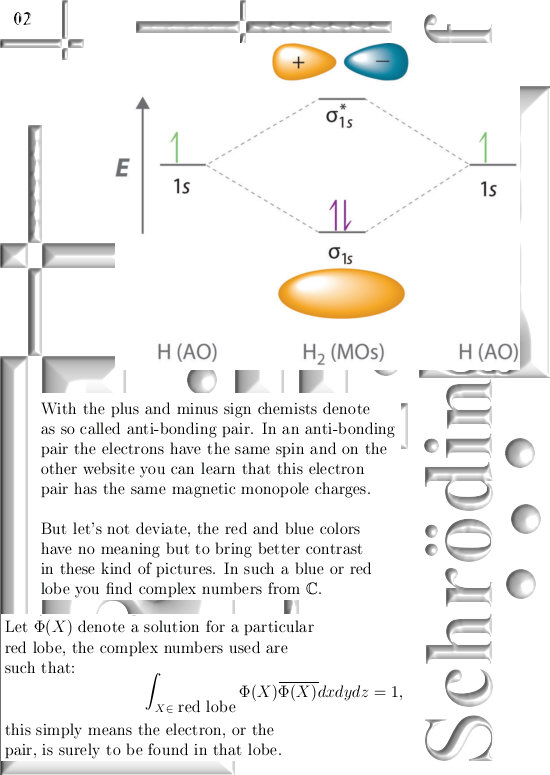
This update is 5 pictures long, size pics = 550 by 775.

__________

One hour later:

Shit! There is a serious problem with uploading the pictures, they get uploaded but they are  not visible… So you must wait at least one day longer because I do not understand the problem at hand…

Till updates.

__________

Problem with the jgp pictures is solved; according to my webhost provider it was caused by the name Schrödinger because that contains an o with two dots: ö.
My computer can handle filenames with ö so for me they looked normal but the server that hosts this website cannot deal with these kinds of symbols…

Anyway after a few days here are the pictures:

0015=28Feb2016=orbital_Schrodinger_post01

0015=28Feb2016=orbital_Schrodinger_post02

0015=28Feb2016=orbital_Schrodinger_post03

0015=28Feb2016=orbital_Schrodinger_post04

0015=28Feb2016=orbital_Schrodinger_post05

Well I am happy this strange problem of invisible pictures has been solved. Till updates.

A new type of Cauchy integral formula.

3D complex numbers, Exponential circle, Exponential curves, Matrix representation

Yesterday I wrote a new post on the Schrödinger equation using 3D complex numbers but before I post that let’s go a bit more hardcore with a brand new Cauchy integral formula.
Actually it is not that brand new because on 18 Jan 2014 I posted it on the other website.

Now in a normal world a brand new Cauchy integral would be greeted with a lot of joy and plenty of discussion, yet that has not happened by now. Once more we observe that among professional math professors there is a severe problem concerning the so called ‘competence question’.
Or may be it is better to frame this into a lack of competence; if you have that you are also not able to judge new results properly and this is what we observe year in year out.

But I have to admit it is a relatively hardcore update, it is 10 pages long and I remember clearly it was fun to write because I wanted to prove the Cauchy formula in this way for a long time.

0014=27Feb2016=Cauchy_integrals

Source: http://kinkytshirts.nl/rootdirectory/just_some_math/3d_complex_stuff02.htm#18Jan2014

__________

Now a person that is not 100% insane might wonder how the hell you calculate the determinant of a six by six matrix because in parctice that is an awful amount of work. But I used an internet applet and as such got a numerical value like about 106,821 and within a few seconds I recognized this as being pi to the power of six divided by nine.

Once back in the year 1992 I came across that number and it was kinda weird to observe that in 2014 it was still floating around in my brain. Sometimes I wonder if I am the crazy one and the math professors are the ones with healthy brains…;)

Ok, till updates my dear reader.

The Cone Theorem.

3D complex numbers, Exponential circle, Matrix representation

On the other website I just posted 12 pages about the cone theorem. This theorem states that cones with a central axis the line through 0 and the number alpha and with their top in 0, undergo a fixed rotation when multiplied by one of the imaginary numbers like j or j^2.

You can find that on page four covering stuff posted this year.

It is important to remark I got the idea to study this particular detail because of the article in the preprint archive from Shlomo Jacobi. Now this Shlomo guy seems to be dead so I have to be a bit cautious. Let’s say these 12 pages are the way should study stuff like this & don’t forget I got the idea from this Jacobi guy while the professional math professors as usual contribute nothing.

In the next teaser picture you see how it works, while calculating some inner product you get this equation and if you fill in some allowed number for the control c you get the desired cone.

These cones are online easily made with an applet named Polyray. The great advantage of this applet is that you can fill in implicit equations so you are not bonded by some explicit stuff like

z = bla bla formulae in x and y.

You can click on the picture to land on the new update (open in a new window):

0013=22Feb2016=teaser_picture_cone_theorem

In another development I posted a few more reasons as why electrons are magnetic monopoles in the magnetic page on the other website. Now lately some folks from MIT have run six simulations of nuclear plasma and the results nicely confirm my insights in the behavior of nuclear plasma.

The MIT folks thought that in a nuclear fusion reactor you could simply neglect the contributions from the electrons because their mass is so small compared to the mass of protons and higher isotopes of atomic hydrogen. But ha ha ha, when electrons are magnetic monopoles such thinking is shallow & hollow. Anyway to make a long story short: the simulations point to a magnetic monopole electron.

Problem is I do not know how they model the plasma in detail, don’t forget the weirdo’s from the universities think electrons are magnetic dipoles and if you think that how can you make a reliable model of plasma anyway???

Here is the link around magnetic monopole stuff:
http://kinkytshirts.nl/rootdirectory/just_some_math/monopole_magnetic_stuff.htm#17Feb2016

Enough of the bla bla bla, may be in the next post on this website I am going to dive into stuff related to the Schrödinger equation. Or something else like thousands and thousands of new and previously unknown trigoniometric identities…

We’ll see, till updates.

Seven properties of the number alpha.

3D complex numbers, Laplacian, Matrix representation

The number alpha is one of my best finds in the field of mathematics. In all kinds of strange ways it connects very different parts of math to one another, for example when it comes to partial differential equations the number alpha plays a crucial role in transforming this of a pile of difficult stuff into something that lives in only one dimension.

You can also use the number alpha for perpendicular projections, you can use it for this and you can use it for that.

__________

Now in the previous post I told you I would write out some of the elementary properties of the number alpha, but when I finished it the thing was about 5 A4 size pages long and that would be about 10 pictures on this new website.

That would be a bit too long and also I had written nothing in the page for 2016 on the other website. So I decided to hang those five A4 pages in the old website and you get a few teaser pictures on this new website.

Here are the three teaser pictures, click on any to land on the alpha update:

0012=09Feb2016=teaser_pics_alpha_properties01

0012=09Feb2016=teaser_pics_alpha_properties02

0012=09Feb2016=teaser_pics_alpha_properties03

The applet I used is a very helpfull tool, you can find it here:
http://calculator.vhex.net/calculator/linear-algebra/matrix-exponential-using-the-pade-approximation

Ok, that was it. Till updates and do not forget to floss your brain a bit every now and then…

Imitators of the complex number i and how this relates to the zero’s of the Riemann zeta function in 3D.

3D complex numbers

The zero’s of the Riemann zeta function is one the things I will never be able to find because I hate it to write computer code. Always my original enthousiasm fades away quickly and after some time I simply stop working in that direction and foces on things that I like more.

Just like a few posts back when I finally decided to skip the stupid Mandelbrot fractal in three dimenstions. Computers are nice things to build but programming has never been my cup of tea let alone my pint of beer. (I am also a hobby brewer, it is a great hobby and it saves you a lot of money. The more you brew the more money you save…).

Ok in this update we are going to take a look at imitators of the number i from the complex plane. I think that most readers here already know that multiplication by i rotates everything 90 degrees. In 3D space we have similar things but not all higher dimensional number spaces contain the number i from the complex plane. In that case we must use substitutes like what I name the ‘imitators of i‘.

This update is seven pictures long, each picture is 550 by 550 pixels:

0011=04Feb2016=imitators_of_i01

0011=04Feb2016=imitators_of_i02

0011=04Feb2016=imitators_of_i03 0011=04Feb2016=imitators_of_i04

0011=04Feb2016=imitators_of_i05

0011=04Feb2016=imitators_of_i06

0011=04Feb2016=imitators_of_i07

In the next post we will flea through the elementary properties of the number alpha, look at the dynamics on the line through zero and alpha (just like on the real line) and so on and so on.
Till updates.