Monthly Archives: July 2021

Oversight of all counter examples to the last theorem of Pierre de Fermat, Part 3.

3D complex numbers, Last Fermat theorem, Matrix representation

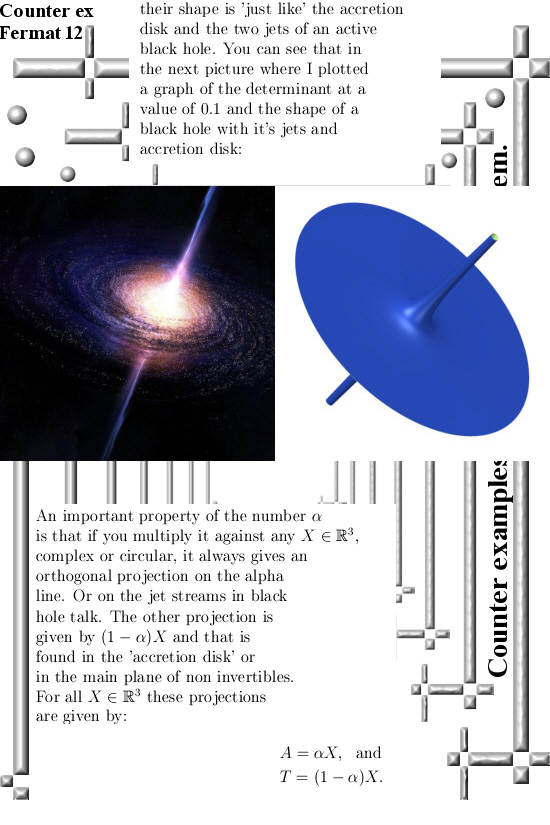
It is late at night, my computer clock says it is 1.01 on a Sunday night. But I am all alone so why not post this update? This post does not have much mathematical depth, it is all very easy to understand if you know what split complex numbers are.
In the language of this website, the split complex numbers are the 2D circular numbers, In the past I named a particular set of numbers complex or circular. I did choose for circular because the matrix representations of circular numbers are the so called circulant matrices. It is always better to give mathematical stuff some kind of functional name so people can make sense of what the stuff is about. For me no silly names like ‘3D Venema positive numbers’ or ‘3D Venema complex numbers’. In math the objects should have names that describe them, the name of a person should not be hanged on such an object. For example the Cayley-Hamilton theorem is a total stupid name, the names of the humans who wrote it out are not relevant at all. Further reading on circulant matrices: Circulant matrix.
I also have a wiki on split complex numbers for you, but like all common sources they have the conjugate completely wrong. Professional math professors always think that taking a conjugate is just replacing a + by a – but that is just too simplistic. That’s one of the many reasons they never found 3D complex numbers for themselves, if you do that conjugate thing in the silly way all your 3D complex math does not amount to much…
Link: Split-complex number.

This is the last part on this oversight of counter examples to the last theorem of Pierre de Fermat and it contains only the two dimensional split complex numbers. When I wrote the previous post I realized that I had completely forgetten about the 2D split numbers. And indeed the math results as found in this post are not very deep, it’s importance lies in the fact that the counter examples now are unbounded. All counter examples based on modular arithmetic are always bounded, periodic to be precise, so professional math professors could use that as a reason to declare that all a bunch of nonsense because the real integers are unbounded. And my other counter examples that are unbounded are only on 3D complex & circular number spaces and the 4D complex numbers so that will be neglected and talked into insignificance because ‘That is not serious math’ or whatever kind of nonsense those shitholes come up with.

All in all despite the lack of mathematical depth I am very satisfied with this very short update. The 2D split numbers have a history of say 170 years so all those smart math assholes can think a bit about why they never formulated such simple counter examples to the last theorem of Fermat… May be the simplicity of the math results posted is a good thing in the long run: compare it to just the natural numbers or the counting numbers. That is a set of numbers that is very simple too, but they contain prime numbers and all of a sudden you can ask thousands and thousands of complicated and difficult questions about natural numbers. So I am not ashamed at all by the lack of math depth in this post, I only point to the fact that over the course of 170 years all those professional math professors never found counter examples on that space.

This post is just 3 pictures long although I had to enlarge the lastest one a little bit. The first two pictures are 550×825 pixels and the last one is 550×975 pixels. Here we go:

That was it for this post, one of the details as why this post is significant is the use of those projector numbers. You will find that nowhere on the entire internet just like the use of 3D complex numbers is totally zero. Let’s leave it with that, likely the next post is about magnetism and guess what? The physics professors still think there is no need at all to give experimental proof to their idea of the electron having two magnetic poles. So it are not only the math professors that are the overpaid idiots in this little world of monkeys that think they are the masters of the planet.

Oversight of all counter examples to the last theorem of Pierre de Fermat, Part 2.

3D complex numbers, 4D complex numbers, Last Fermat theorem

Post number 191 already so it will be relatively easy to make it to post number 200 this year. If you think about it, the last 190 posts together form a nice bunch of mathematics.
In this post we will pick on where we left it in the last post; we start with the three dimensional complex and circular numbers. In the introduction I explain how the stuff with a pair of divisors of zero works and from there it is plain sailing so to say. When back in Jan of this year I constructed the first counter example to the last theorem of Pierre de Fermat I considered it a bit ‘non math’ because it was so easy. And when one or two days later I made the first counter example using modular arithmetic I was really hesitant to post it because it was all so utterly simple…
But now half a year later it has dawned on me that all those professional math professors live up to their reputation of being overpaid under performers because in a half year of time I could find not one counter example on our beloved internet. And when these people write down some calculations that could serve as a counter example, they never say so and use it only for other purposes like proving the little theorem of Fermat. It has to be remarked however that in the past three centuries of time, when people tried to find counter examples, they likely started with the usual integers from the real line and as such tried to find counter examples. Of course that failed and this is not because they are stupid or so. It is the lack of number spaces they understand or know about that prevented them in finding counter examples to the last theorem of Pierre de Fermat.
If you do not know anything about 3D complex or circular numbers, you are not a stupid person if you cannot find counter examples to the last theorem. But you are definitely very very stupid if you do not want to study 3D complex numbers, if you refuse that it proves you have limited mathematical insights and as such likely all your other math works will be limited in long term value too.
While writing this post all of a sudden I realized I skipped at least one space where counter examples are to be found: It is on the space of so called split complex numbers. I did not invent that space, that was done by the math professors. The split complex numbers are a 2D structure just like the complex plane but instead of i^2 = -1, on the split complex plane the multiplication is ruled by i^2 = 1. Likely I will write a small post about the split complex number space. (Of course in terms of the language of this website, the 2D split complex numbers are the 2D circular numbers.)

This post is 8 pictures long, I kept on to number them according to the previous post so we start at picture number 11. They are all in the size of 825×550 pixels. I hope it is worth of your time. Here we go:

In this post I used only ‘my own spaces’ like 3D complex and circular numbers and the 4D complex numbers. As such it will be 100% sure the math professionals will 100% not react on it. Even after 30 years these incompetents are not able to judge if there is any mathematical value in spaces like that. Why do we fork out so much tax payer money to those weirdo’s? After all it is a whole lot of tax payer money for a return of almost nothing. Ok ok a lot of math professors also give lectures in math to other studies like physics so not all tax payer money is 100% wasted but all in all the math professors are a bunch of non-performers.

I think I will write a small post about the 2D split complex numbers because that is a space discovered by the math pro’s. So for them we will have as counter examples to the last theorem of Pierre de Fermat all that modulo calculus together with the future post on the split complex numbers. Not that this will give a reaction from the math pro’s but it will make clear you just cannot blame me for the non reactive nature of the incompetents; the blame should go to those who deserve it… Or not?

May be the next post is about magnetism and only after that I will post the split complex number details. We’ll see, anyway if you made it untill here thanks for your attention and I hope you learned a bit from the counter examples to the last theorem of Pierre de Fermat.