Monthly Archives: January 2024

That mysterious electron pair and so called VESPR theory.

Magnetism

Some time ago I stopped writing posts about magnetism because the number of such posts would exceede the number of posts on the 3D complex numbers. And that was of couse not the long term strategic goal of this website, so I stopped posting it here.
But on the other website I kept on writing small sniplets and what I consider the best two sniplets is now reposted here in a new post on magnetism.

For readers who are new: For the last 9 years I have been trying to figure out if electrons are truly tiny magnets yes or no. About 9 years ago I started to doubt that electrons or electron spin is indeed a bipolar magnet. At the time I tried to explain the results from the Stern-Gerlach experiment and I arrived at the conclusion that very likely electrons were magnetic monopoles. My main argument has been all those years: If electrons are magnetic dipoles, because they are so small they must be neutral under application of (large) magnetic fields.

Since the SG experiment it is know that lone electrons are not magnetically neutral but all and everything observed was always explained by electrons as tiny magnets. Why at the time (1922 and later) they never observed that there are all kinds of problems with electron spin as tiny magnets, is unknown to me. For example the scientists at the time had correspondence between each other and some of those letters literally started with the Gauss law for magnetism and stating that a solution must be found inside the framework of the Gauss law for magnetism…

It never dawned on them that doing science is that you must prove the Gauss law for magnetism does apply for lone or unpaired electrons. But they never did that, no one doubted that magnetism was without magnetic charges and as such even a very small particle like the electron had to be a tiny magnet.

Since last year I often phrase my view on electron magnetism as follows:

The magnetic properties of the electron are just like it’s electric properties: Permanent and Monopole.

It is a bit strange that after 9 years I still have to try and find nice sounding slogans like the above as if I were some marketing bureau.

Anyway one of the big mysteries of the official version of electron spin is that in an electron pair the spins must be opposite. Nobody remarks this is totally crazy because if we allow for that we also give up the observation that opposite charges atract while same charges repel. I made an extra picture for this weird official version of electron spin:

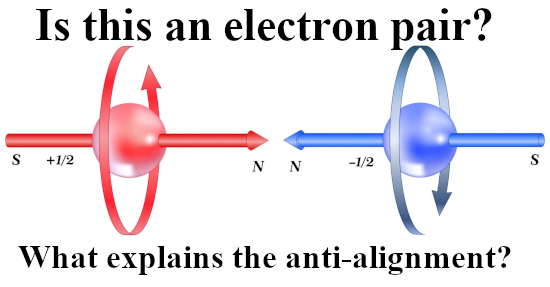
Well take your time to think about it, this is the official version of the electron pair if electrons were tiny magnets. The physics professors never ever mention such details, no you often get a boatload of complicated math but they never ever talk about what anti alignment for tiny magnets actually means.

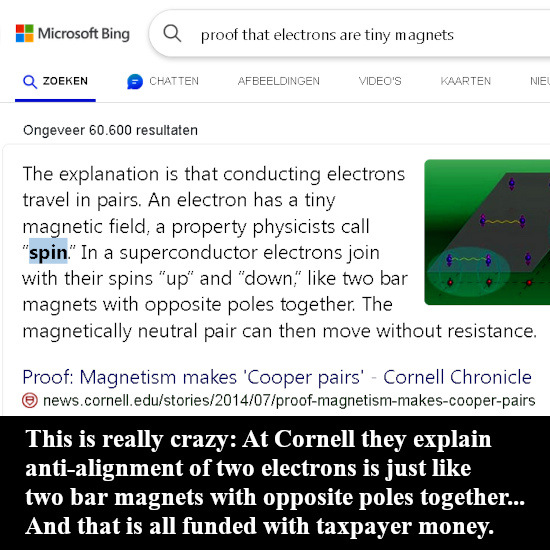
I also want to remark that journalists never ever ask such questions when they interview physics professors on magnetic related stuff. It’s fucking taxpayer money and we must believe this kind of crap?
Well yes, according to Cornell university we must. The next picture is one I actually used on the other website:

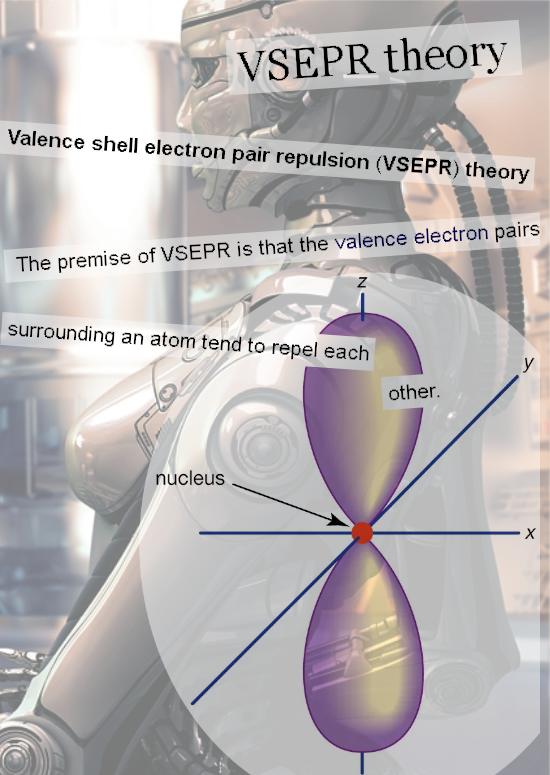
You don’t make this nonsense up: Like two bar magnets with opposite poles together.

VESPR theory. VESPR stands for Valence Electron Shell Pair Repulsion. This theory comes a bit more from the chemical sciences where they try to explain the shapes of the electron clouds of atoms and molecules.

The important detail is that electron pairs are neutral to magnetism and that as such electron pairs around an atomic nucleus repel each other.

If you use the idea that electrons are magnetic monopoles this all is very logical: Coulomb forces pull electrons in and the electrons form pairs because they have opposite monopole magnetic charges.

If you use the idea that electrons are tiny magnets this all is very crazy: Coulomb forces pull electrons in and they only form pairs? Why not form other configurations that are possible with tiny magnets? Why only electron pairs my dear physics professors?

My dear reader you have a brain for yourself so look in the picture below as why this particular atomic nucleus has two electron pairs that repel each other. And don’t mind the female robot or ponder the question as why there are female robots at all…
Just think a bit around the nonsense that comes along with electrons being tiny bipolar magnets. Here is the picture as used on the other website:

It’s time to publish this post, thanks for your attention and see you in a next post.

Two parametrizations for the ‘unit’ ellipse in the i^2 = -1 + i kind of multiplication.

2D multiplications, 3D complex numbers, Exponential circle, Exponential curves

Basically this post is just two parametrizations of an ellipse, so all in all it should be a total cakewalk… So I don’t know why it took me so long to write it, ok ok there are more hobbies as math competing for my time. But all in all for the level of difficulty it took more time as estimated before.
In the last post we looked at the number tau that is the logarithm for the imaginary unit i and as such I felt obliged to at least base one of the parametrizations on that. So that will be the first parametrization shown in this post.
The second one is a projection of the 3D complex exponential on the xy-plane. So I just left the z-coordinate out and see what kind of ellipse you get when you project the 3D exponential circle on the 2D plane. Acually I did it with the 3D circular multiplication but that makes no difference only the cosines are now more easy to work with. Anyway the surprise was that I got the same ellipse back, so there is clearly a more deeper lying connection between these two spaces (the 3D circular numbers and these 2D complex multiplication defined by i^2 = -1 + i).
A part of the story as why there is a connection between these spaces is of course found into looking at their eigenvalues. And they are the same although 3D complex numbers have of course 3 eigenvalues while the 2D numbers have two eigen values. A lot of people have never done the calculation but the complex plane has all kinds of complex numbers z that each have eigenvalues too…
Anyway I felt that out of this post otherwise it would just become too long to read because all in all it’s now already 10 images. Seven images with math made with LaTex and three additional figures with sceenshots from the DESMOS graphical package.
By the way it has nothing to do with this post but lately I did see a video where a guy claimed he calculated a lot of the Riemann zeta function zero’s with DESMOS. I was like WTF but it is indeed possible, you can only make a finite approximation and the guy used the first 200 terms of the Riemann zeta thing.
At this point in time I have no idea what the next post will be about, may be it’s time for a new magnetism post or whatever what. We’ll wait and see, there will always pop something up because otherwise this would not be post number 254 or so.
Well here is the stuff, I hope you like it or enjoy it.

Figure 1: This parametrization is based on the number tau.
Figure 2: The projection in red, stuff without 1/3 and 2/3 in blue.
Figure 3: The end should read (t – 1.5) but I was to lazy to repair it.

That was it for this post, of course one of the reasons to write is that I could now file it under the two categories “3D complex numbers” and “2D multiplications” because we now have some connection going on here.
And I also need some more posts related to 3D complex numbers because some time ago I found out that the total number of posts on magnetism would exceed those of the 3D complex numbers.

And we can’t have that of course, the goal of starting this website was to promote 3D complex numbers via offering all kinds of insights of how to look at them. The math professors had a big failure on that because about 150 years since Hamilton they shout that they can’t find the 3D complex numbers. Ok ok, they also want it as a field where any non-zero number is invertible and that shows they just don’t know what they are talking about.
The 3D complex numbers are interesting simply because they have all those non-invertible numbers in them.

It is time to split my dear reader so we can both go our own way so I want to thank you for your attention.