Basically this post is just two parametrizations of an ellipse, so all in all it should be a total cakewalk… So I don’t know why it took me so long to write it, ok ok there are more hobbies as math competing for my time. But all in all for the level of difficulty it took more time as estimated before.
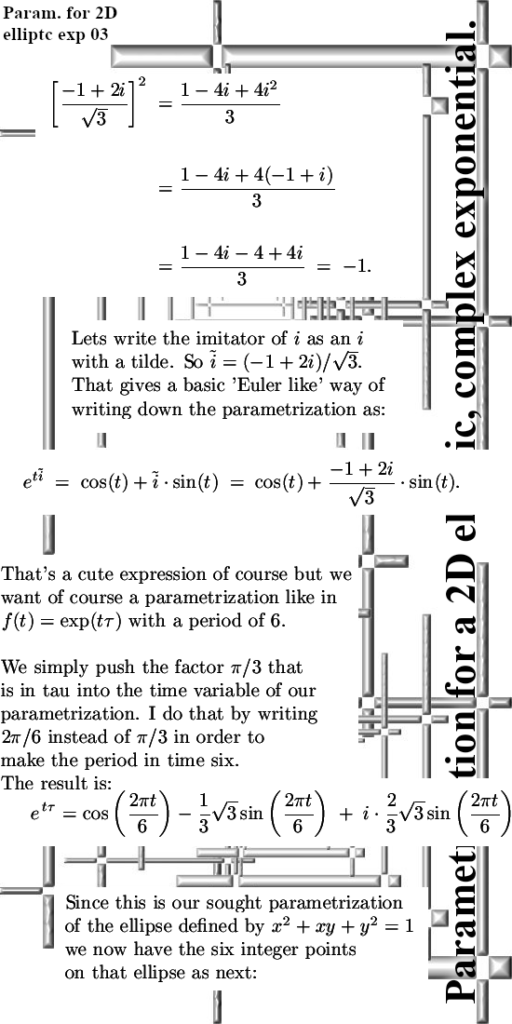
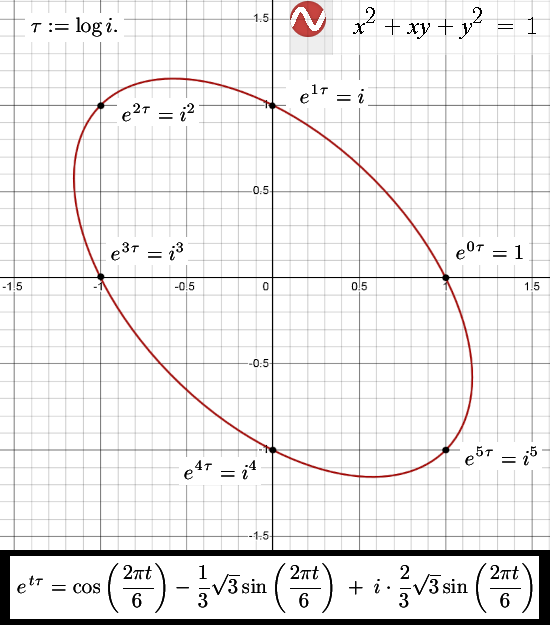
In the last post we looked at the number tau that is the logarithm for the imaginary unit i and as such I felt obliged to at least base one of the parametrizations on that. So that will be the first parametrization shown in this post.
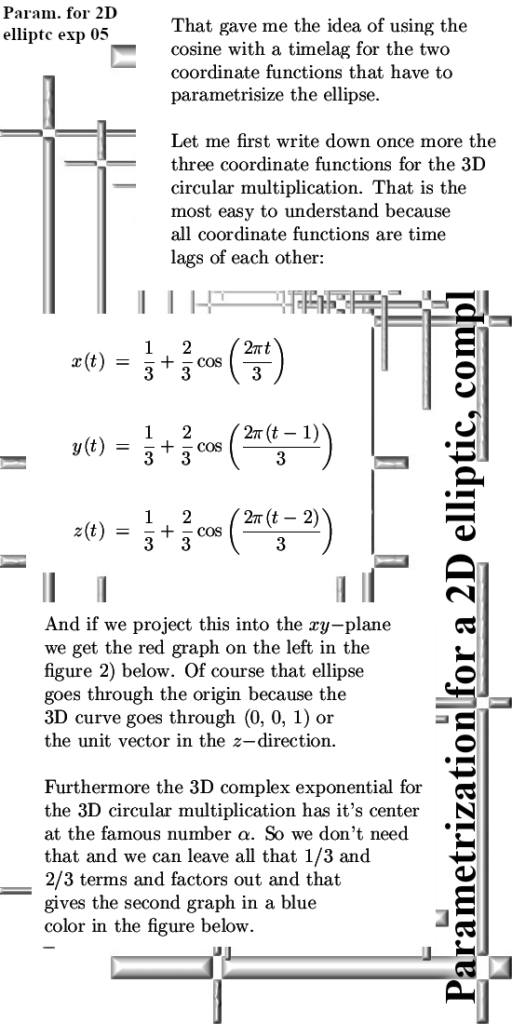
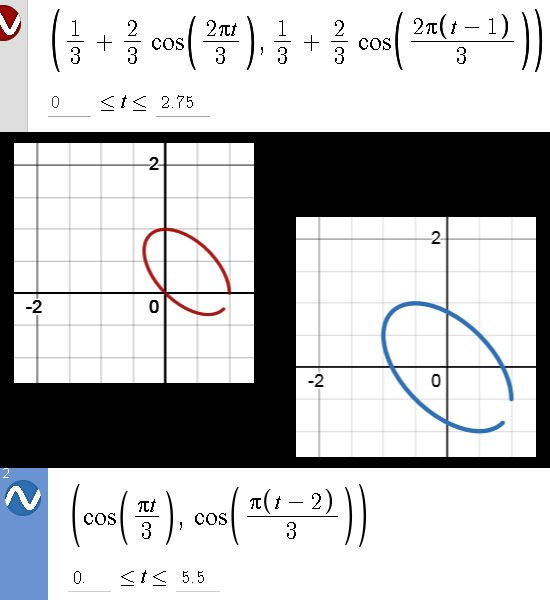
The second one is a projection of the 3D complex exponential on the xy-plane. So I just left the z-coordinate out and see what kind of ellipse you get when you project the 3D exponential circle on the 2D plane. Acually I did it with the 3D circular multiplication but that makes no difference only the cosines are now more easy to work with. Anyway the surprise was that I got the same ellipse back, so there is clearly a more deeper lying connection between these two spaces (the 3D circular numbers and these 2D complex multiplication defined by i^2 = -1 + i).
A part of the story as why there is a connection between these spaces is of course found into looking at their eigenvalues. And they are the same although 3D complex numbers have of course 3 eigenvalues while the 2D numbers have two eigen values. A lot of people have never done the calculation but the complex plane has all kinds of complex numbers z that each have eigenvalues too…
Anyway I felt that out of this post otherwise it would just become too long to read because all in all it’s now already 10 images. Seven images with math made with LaTex and three additional figures with sceenshots from the DESMOS graphical package.
By the way it has nothing to do with this post but lately I did see a video where a guy claimed he calculated a lot of the Riemann zeta function zero’s with DESMOS. I was like WTF but it is indeed possible, you can only make a finite approximation and the guy used the first 200 terms of the Riemann zeta thing.
At this point in time I have no idea what the next post will be about, may be it’s time for a new magnetism post or whatever what. We’ll wait and see, there will always pop something up because otherwise this would not be post number 254 or so.
Well here is the stuff, I hope you like it or enjoy it.





That was it for this post, of course one of the reasons to write is that I could now file it under the two categories “3D complex numbers” and “2D multiplications” because we now have some connection going on here.
And I also need some more posts related to 3D complex numbers because some time ago I found out that the total number of posts on magnetism would exceed those of the 3D complex numbers.
And we can’t have that of course, the goal of starting this website was to promote 3D complex numbers via offering all kinds of insights of how to look at them. The math professors had a big failure on that because about 150 years since Hamilton they shout that they can’t find the 3D complex numbers. Ok ok, they also want it as a field where any non-zero number is invertible and that shows they just don’t know what they are talking about.
The 3D complex numbers are interesting simply because they have all those non-invertible numbers in them.
It is time to split my dear reader so we can both go our own way so I want to thank you for your attention.