An inverse and a number tau for the i^2 = -1 + i multiplication.

2D multiplications

This way of doing the complex multiplication keeps on drawing my attention because of the funny property that i^3 = -1. As such it has interesting parallels to the 3D complex number. For example the eigenvalues of this defining imaginary unit is the third root out of -1 (and it’s conjugate). That is in line with the results from the 3D numbers although over there 3D numbers have 3 eigenvalues and not 2.

In this post I want to show you a way to find the logarithm of this imaginary unit i via integrating the inverse from 1 to i. Just like on the real line if you integrate 1/x from 1 to say some positive a, you get log a. It is important to remark there are more methods to find such logarithms. For example you can diagonalize the multiplication and take the log of the eigenvalues and as such you can find the log of the imaginary unit.

Anyway back in the time I did craft my first complex exponential for the 3D complex numbers this way (using the integral of the inverse) so for me it is a bit of a walk down memory lane. You always get integrals that are hard to crack but if you use the WolframAlpha website it’s easy to find. Remarkably enough the two values for the integrals we will find below are also found in 3D and even the 6D complex numbers. So for me that was something new.

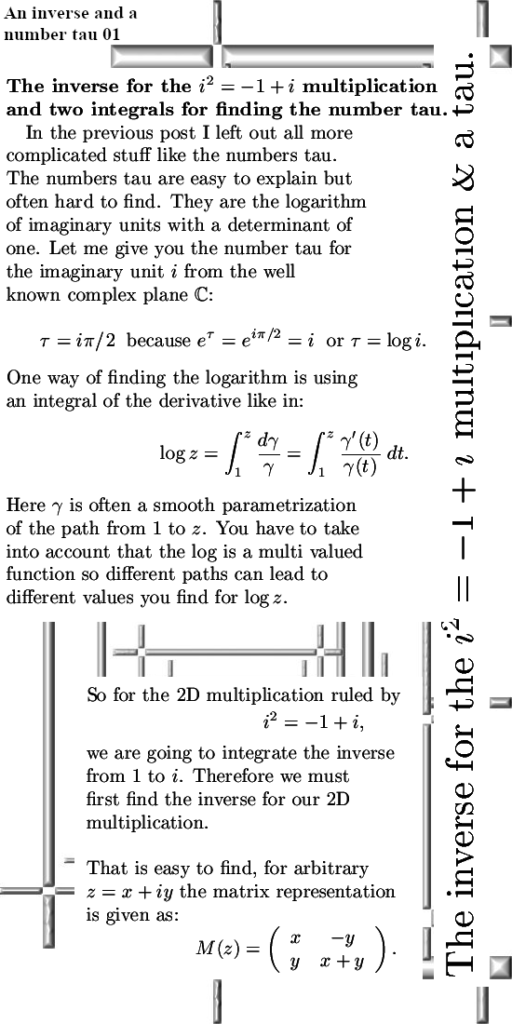
For myself speaking I loved the way the inverse of a complex number based on i^2 = -1 + i looks. You have to divide by the determinant once more proving that norms do not have very much to do with it. (In standard lessons on complex numbers it is always told that the norm of the product is the product of the norms, but that’s only so for the complex plane and the quaternions. So if you keep on trying such idea’s you won’t come very far…)

This post is five pictures long, lets go:

May be this parametrization is the next post.

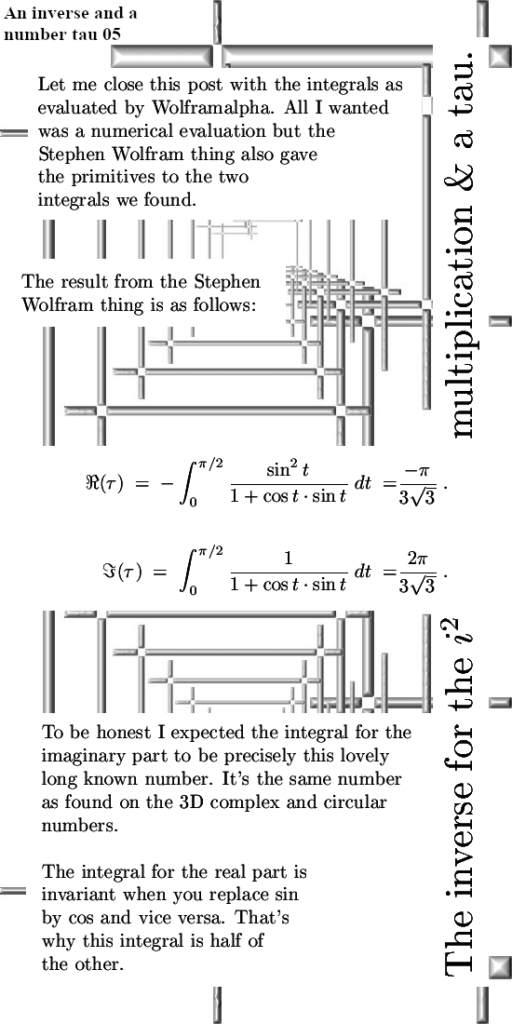
Ok, that was it more or less for this post. Since we are now getting more and more posts on two dimensional complex (and split complex) numbers may be I will open a new category for those posts. On the other hand you must not open a new category every time you things that are a bit different from what you usually do…