Monthly Archives: October 2016

Derivation of the number tau for the circular 3D number system.

3D complex numbers, Exponential circle, Matrix representation

There are lot’s of reasons for this update; one reason is that the actual calculation is mega über ultra cool. Another important reason is that this collection of plain imitation of how the value for the number i in the complex plane was found serves as a proof in itself that this way of crafting 3D complex and circular numbers is the only way it works.

Don’t forget that on the scale of things the Irish guy Hamilton tried for about a decade to find the 3D numbers but he failed. Yet Halmilton was not some lightweight, the present foundation of Quantum Mechanics via the use of the Hamilton operator is done so via the work of Hamilton…
Wether the professional math professors like it or not; that is the scale of things.

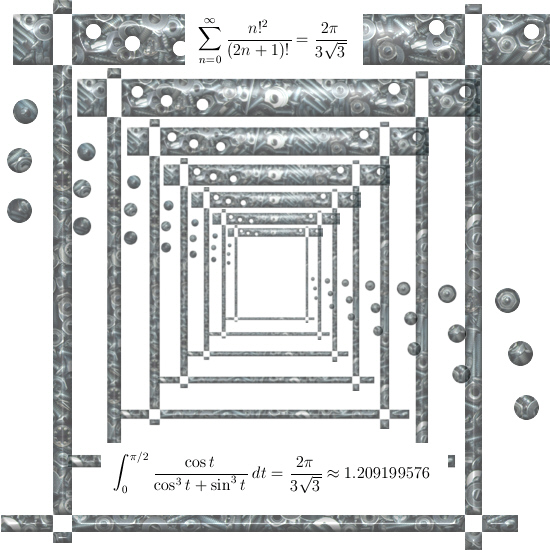
During the writing of this post I also got lucky because I found a very cute formula related to the so called Borwein-Borwein function. I have no clue whatsoever if it has any relevance to my own work on this website but because it is so cute I just had to post it too…

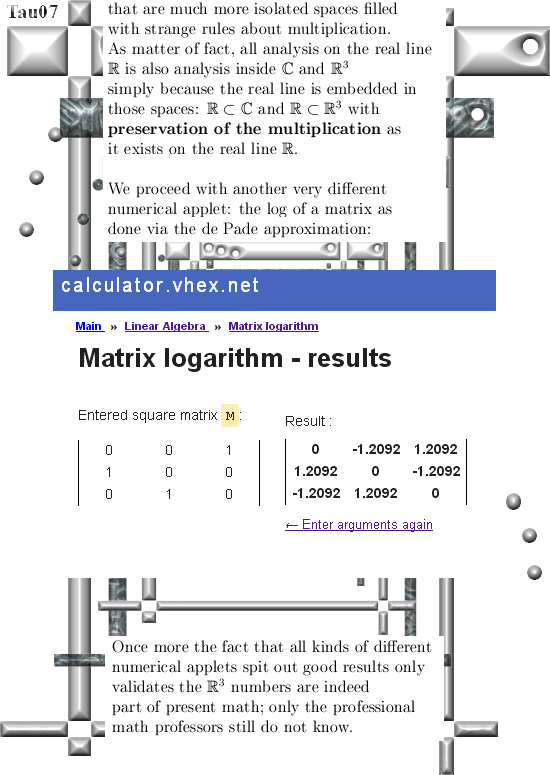
Furthermore I used two completely different numerical applets, one for integration and the other for evaluating the log of a matrix, only to show you that these kind of extensions of the complex plane to three dimensional space is the way to go and all other approaches based on X^2 = -1 fail for the full 100%.

__________

This post is ten pictures long, size 550 x 775 pixels.

At the end I will make a few more remarks and give you enough links for further use in case you want to know more about this subject. Have fun reading it.

22oct2016-calculation-of-the-circular-tau01

22oct2016-calculation-of-the-circular-tau02

22oct2016-calculation-of-the-circular-tau03

22oct2016-calculation-of-the-circular-tau04

22oct2016-calculation-of-the-circular-tau05

22oct2016-calculation-of-the-circular-tau06

22oct2016-calculation-of-the-circular-tau07

22oct2016-calculation-of-the-circular-tau08

22oct2016-calculation-of-the-circular-tau09

22oct2016-calculation-of-the-circular-tau10The applet for the logarithm of a matrix can be found in this nice collection of linear algebra applets:

Linear algebra
http://calculator.vhex.net/function-index/linear-algebra

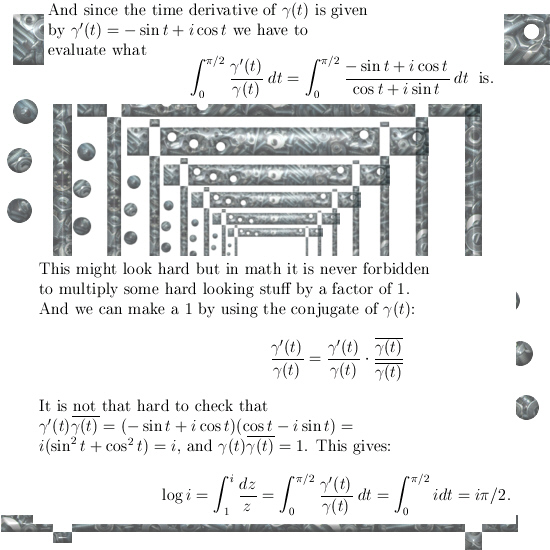
In this update you might think that via the pull back principle you observed some proof for the value of the integrals we derived, but an important detail is missing:
In 3D space the exponential circle should be run at a constant speed.
As a matter of fact this speed is the length of the number tau, you can find more insight on that in the theorem named ‘To shrink or to grow that is the question’ at:

On the length of the product of two 3D numbers.
http://kinkytshirts.nl/rootdirectory/just_some_math/3d_complex_stuff04.htm#06May2016

A bit more hardcore is my second proof of the value of the integrals as derived in this post. On 15 Nov 2015 I published the second proof that I found while riding on my bicycle through the swamps near a local village named Haren. It is kinda subtle but you can use matrix diagonalization to get the correct answer.
The reaction from the ‘professional community of math professors’ was the usual: Zero point zero reaction. These people live in a world so far away from me: overpaid and ultra stupid…

Integral calculus done with matrix diagonalization.
http://kinkytshirts.nl/rootdirectory/just_some_math/3d_complex_stuff03.htm#21Nov2015

A link to the online encyclopedia of integer sequences is the next link.
Remark that by writing the stuff as on-line instead of online reflects the fact this website must be from the stone age of the internet. That is why it can have this strange knowledge…

The On-Line Encyclopedia of Integer Sequences
https://oeis.org/ (Just fill in 1, 2, 0, 9, 9, 5, 7 in order to land on my lucky day).

The last link is one of those pages that try to explain as why 3D complex numbers cannot exist, the content of this page is 100% math crap written by a person with 0% math in his brain. But it lands very high in the Google ranking if you make a search for ‘3D complex numbers’.
So there must be many people out there thinking this nonsense is actually true…

N-DIMENSIONAL COMPLEX NUMBERS.
http://www.alenspage.net/ComplexNumbers.htm

Ok, this is what I had to say. Let me close this post, hit the button ‘update website’ and pop up a fresh beer… Till updates.

Too little time left so only a second teaser picture on the next post on the details of the 3D tau calculus.

Uncategorized

Originally I planned to upload tonight the new post on the integrals related to the number tau for the circular multiplication. But I found this very cute result from some other math professors, I believe these are two brothers Borwein & Borwein.

Beside that I also had more time to spend on a very important hobby: Brewing beer…;)

Four years back when I for the first time derived integrals like this with the cosine and sine stuff to the power three in it, I just had no clue whatsoever how to find analytical stuff for their value. These kind of integrals cannot be solved by throwing in some simple primitive or so.

At present I have two independent proofs for their value.
Back in the time I knew there was some internet website that contains a whole lot of integer sequences so if I could find that I would have at least some analytical clue about that nasty problem. Only a long time later I found that website, but is said ‘we do not know’.
Or ‘unknown integer sequence’ or whatever what.

But yesterday when I tried more or less to get a negative result my luck changed for the better: the website with the integer sequences in it actually returned an answer.

And for my few pounds of human brain tissue the answer was completely crazy.
Therefore I decided to put the result of this Borwein function on top in the teaser picture and my own idea’s at the bottom. Here it is:

20-10-2016-borwein-borwein-teaser-pictureI have absolutely no clue as why these two things should be the same, but four years back I had absolutely no clue as what this numerical value like 1.2092 actually meant…

The link to what might be the Borwein & Borwein function

A248897 Decimal expansion of Sum_{i >= 0} (i!)^2/(2*i+1)!.
https://oeis.org/A248897

Let’s leave it with that, see ya in the next post.

Three new magnetics updates + Intro to a new post about calculation of the number tau.

Magnetism, Uncategorized

On the other website I posted reason number 37, 38 and 39 about why it is impossible for electrons to be magnetic dipoles. Let me give you the links and short descriptions about their content.

05 Oct 2016: Reason 37: Old and new experiments upon the bonkers force.
http://kinkytshirts.nl/rootdirectory/just_some_math/monopole_magnetic_stuff.htm#05Oct2016

Once more the importance of repeatable experiments is stressed; my own simple experiments with that old color television is explained once more. Furthermore I am proposing a few other experiments that I cannot do here myself because, for example, they should be done is a space without magnetic or electrical fields.

The thing ‘bonkers force’ is acting along the magnetic field lines and makes electrons (and protons etc) accelerate. So it is perpendicular to the Lorentz force.

10 Oct 2016: Reason 38: The Hendrik Casimir effect and the vacuum catastrophe.
http://kinkytshirts.nl/rootdirectory/just_some_math/monopole_magnetic_stuff.htm#10Oct2016

The Nobel prize in physics went this year to three men who studied two dimensional structures of electrons. So with just 50 to 70 minutes of labor I managed to do the same and explain as why the experiment of Hendrik Casimir has a wrong experimental set up because there they use the idea that electrons are magnetic dipoles. En passant using this wrong set up of Hendrik Casimir I can explain the root cause of the so called ‘vacuum catastrophe’.
The theoretical value of the so called zero-point energy of one cubic centimeter of space should be 10 to the power 112 erg of energy, yet at present day the best value found is about 10 to the power -8.

That is off the mark by just a factor of 10 to the power 120…

14 Oct 2016: Reason 39: The acceleration of the solar wind.
http://kinkytshirts.nl/rootdirectory/just_some_math/monopole_magnetic_stuff.htm#14Oct2016

This is just one of the many things you cannot explain with electrons and protons being magnetic dipoles; despite gravity and or the influence of electrical fields the solar wind does not go down in speed. The professional physics professors cannot explain this nasty detail because they keep on holding on to the Gauss law for magnetism that says magnetic monopoles do not exist…

For the electron pair the Gauss law is valid but not for loose electrons.
As far as I know the winners of the Nobel prize from this year also believe electrons are magnetic dipoles so the Nobel committee has done a great disservice to the progress in physics.

So from the vacuum catastrophe to the properties of the solar wind: the professional physics professors will not find an explanation century in century out because you must not think that by writing down how stuff likely works they will change their ways.

But, ha ha ha my dear but incompetent and coward physics professors: My experiment with an old television can be repeated by any person and you, you fxckheads, cannot explain it…

__________

Ok, we proceed with math: The next post will be about how to find the number tau that you must use for crafting exponential circles and curves in dimensions above 3.

In order to focus the mind I would like to repeat a rather famous calculation from the complex plane: the calculation of the logarithm of the imaginary number i.
It is a beautiful calculation and it says that log i = i*pi/2.

Three teaser pictures to ram home to the brains of professional physics professors that I know plenty of complex numbers and that in my view using only 2D complex numbers simply shows what kind of brain matter you folks are made of:

16oct2016-famous-math-calculation01

16oct2016-famous-math-calculation02

16oct2016-famous-math-calculation03

At the closing of this small update I would like to remark that in the next post we are going to try and find logarithm values for imaginary numbers from 3D space.

And if in the future the Nobel committee would select Nobel prize winners that can actually think deeply and not all this shallow stuff, that would be great!

See you around my dear reader, till updates.