Category Archives: 2D multiplications

Two parametrizations for the elliptic complex number done in the Euler style.

2D multiplications, Exponential curves

This is a follow up from a post from Jan 2024 that also has ‘two parametrizations’ in the title but that were two parametrizations of the same ellipse and in this post I look at two ellipses. So this post is a bit of a repeat and a bit of new stuff. You can always use the search function of this website to find that old post and I can also link to it:

Two parametrizations for the ‘unit’ ellipse in the i^2 = -1 + i kind of multiplication.

Ok, all in all this is not a very ‘important’ post like lately when I showed you how you can do integration in say 3D space using a primitive. But I considered the two parametrizations elegant enough to write this new post about them.
In the post from Jan 2024 I showed you how to parametrize or cover the complex ellipse with two cosines with a time lag of one third of a period between them. The unit circle in the complex plane can be viewed as two cosines with a quarter of a time lag between them because that transforms a cosine into a sine and you get the familiar expression for the complex exponential.

This post is six images long and I added three appendices to it for the graphs that hopefully make all the stuff a bit more transparant. I hope you like it and that we are not in a situation where say in half an hour your neighbors phone the police one more time with “He is shouting at the mirror again, please come help and save us”. Ok, here we go:

As you see it’s not very hardcore but it is all relatively simple. Just some covers of two ellipses. Thanks for your attention.

Two times the number tau for the 2D elliptic complex numbers.

2D multiplications, Exponential circle, Exponential curves, Integration

Throughout this entire website numbers tau are always the logarithm of a suitable imaginary unit. Of course this depends on the kind of space you are in, the higher the dimension the more difficult they become to calculate. Here is the dimension as low as possible with only 2 dimensions, in this post and all other posts on the elliptics they are always 2D and in this post I only look at the imaginary unit i and the multiplication they define are as usual:
i^2 = -1 + i, this gives the elliptic complex numbers. And if we do
i^2 = -1 – i that gives the split elliptic numbers.

Try it yourself: The third power of these imaginary units are -1 in the first case and the third power is +1 for the split elliptic numbers. That is why I name those the split complex numbers, just like there are ordinary complex and split complex numbers are defined by i^2 = +1.

The basic idea behind this post is that the derivative of the log equals the inverse and the other way around: integration of the inverse must yield the logarithm. Of course outside the real line complex exponentials can have periods and sometimes people use that to say the log is a multi valued function. That is also why people often leave a cut out of the complex plane, for example the complex plane without the negative real numbers. Now the log is not multi valued. Well I skip all such considerations and beside that in this post we only calculate a number and we do not study the log in itself.

So integration of the inverse in a 2D number system, that’s basically what this post is. It is more or less the royal road paved with silver and gold that leads to defining complex exponentials while as we will see in the next post that if we want to parametrize these complex exponentials we don’t need knowledge about the actual number tau at all.

This post is seven images in itself and one addendum so 8 images in total.

That was it for this post, thanks for your attention and I hope you liked it a bit. Or may be you didn’t vomit at all and that would also be a great thing, that would still be progress although may be you didn’t like it like I hoped for… Enough of this silly talk, let me upload the whole bunch and see you in a future post.

Two versions of the 2D elliptic complex numbers.

2D multiplications, Matrix representation

The main reason for me writing this post is once more showing you how to take a conjugate when it is not as simple as “A reflection into the x-axis”. I am now in my sixties when it comes to my age and to be honest in my entire life I have never seen just one person doing it right. All they do is flip it into the x-axis and when their calculations derail they just throw away the whole thing and never think twice about what they are doing.

A better way of formulating a conjugate is the next: Replace all imaginary units by their inverse. And yes, in case of the standard 2D complex plane that is a reflection in the x-axis. But that does not mean that in every space where a conjugate is a meaningful thing it will be a reflection. In the case of this post it surely is not a reflection and likely that is the reason that these kind of elliptic complex numbers are completely unknown to the professional math profession. In that regard it is the same as say the 3D complex numbers; also completely unknown because they are to stupid to adjust the math when that’s needed. In some highly autistic version of reality the conjugate must be a flip in the real axis and these people are totally blind for what they do wrong.

This post is five images long and an extra addendum with the two graphs of the ellipses that form the complex exponential on these two relatively simple spaces. May be the next post is about finding those famous numbers tau, on this entire website a number tau is always the logarithm of a suitable imaginary unit. Because a 2D number space is very simple we have only one imaginary unit of course written as i and tau is the log of i.

The direction of the tangents in the point z = 1 is the direction of the number tau. That is a simple yet effective idea from Sophus Lie who a long long time ago invented those things we now know as Lie algebra’s and Lie groups. So on the one hand if you already know what tau is, all you do is differentiate the complex exponential. And if you haven’t found the precise value for tau you can always use implicit differentiation on the equations that define the complex exponential, in this case the equations for the two ellipses. You can use that for checking your calculations for the number tau because those calculations have a strong tendency to run if the rails but if you get the wrong direction you now know there must be a calculation error somewhere…

Ok that was it for this post and this is the 300-th post on this website. As you might have noticed I don’t write more or less two posts a months, only about one. With 300 posts on higher dimensional number systems I have done enough and there is no use in repeating things over and over again. That was it for this post, as always thanks for your attention.

Cauchy-Riemann equations and integration: Part II.

2D multiplications, 3D complex numbers, 4D complex numbers, CR equations, Integration

I made another math post with only differentiating the square function and integrating the identity function like in integrating zdz on the complex plane. This post is much shorter, only 7 images long and one appendix so all in all 8 images.
One of the reasons I decided to write another post on this relative simple stuff is that historically speaking the square was the thing that gave the complex plane. And for some reason professional math people are completely fixated on that when they try for example find 3D complex numbers: It has to be based on some stuff with a square. Just like say the 4D quaternions from Hamilton: Basically it’s all based on the squares of the three imaginary components and an extra rule for multiplying different imaginary units.

Without much ado let me hang in the 8 images:

It is no secret that inside the profession of math at the universities they can only perform integration with a primitive when it comes to the real line and the complex plane. In the last two posts I showed you again and again how to do this on other spaces. Will the professional community ever change ways and include more spaces where you can perform integration ‘Just like on the real line’? No, after all these are university people and as such it is mostly a giant balloon of hot ego air and not much substance when it comes to math.

By accident I came across a work of professor Tom who happily informs his audience of the miracles of the 4D quaternions. You know for me math is a hobby, it’s an important hobby but it’s just a hobby. And because after all the subject is math I take it seriously. But decade in decade out the only thing professional math professors do is fuck around and that’s it.
Here’s the link to the garbage from professor Tom:
Stop 3: Multi-dimensional World
These people just never make any kind of progress, if it’s the year 1990 or the present 2026 it just does not matter. They can’t go beyond the square and also they are very unwilling to go beyond the square.
Let me leave my little rant with that, here’s what missing in literally all texts on quaternions: The square of a quaternion…

Ok that was it for this latest post. Likely the next post is one on magnetism in particular electron pairs in chiral molecules. Thanks for your attention.

On the number of integer solutions on the ellipse x^2 + xy + y^2 = N.

2D multiplications

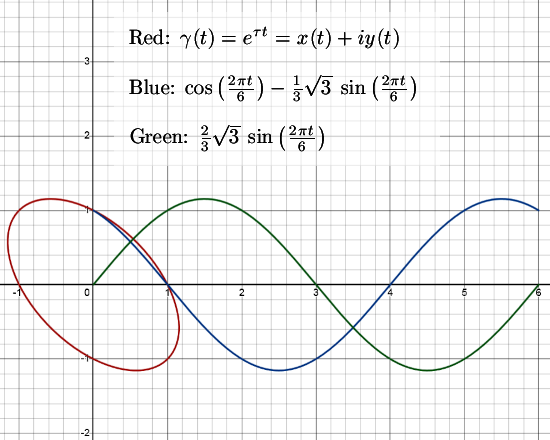
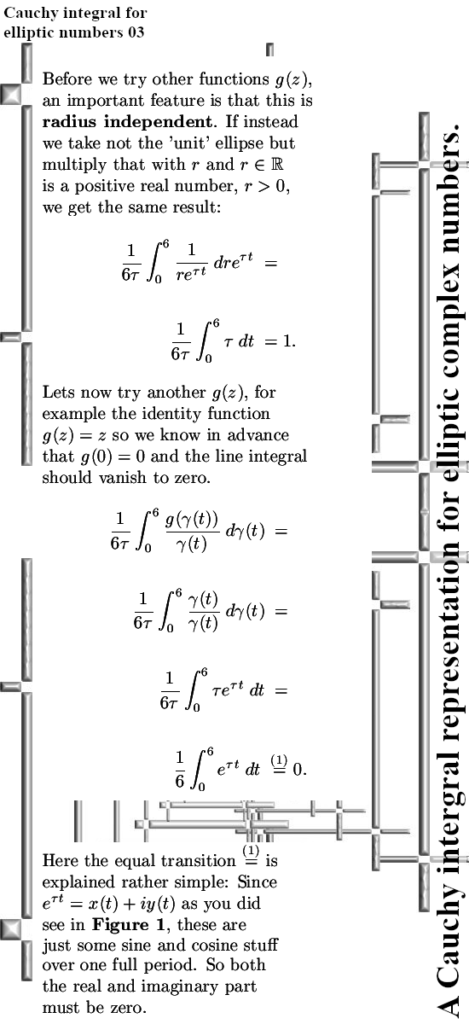
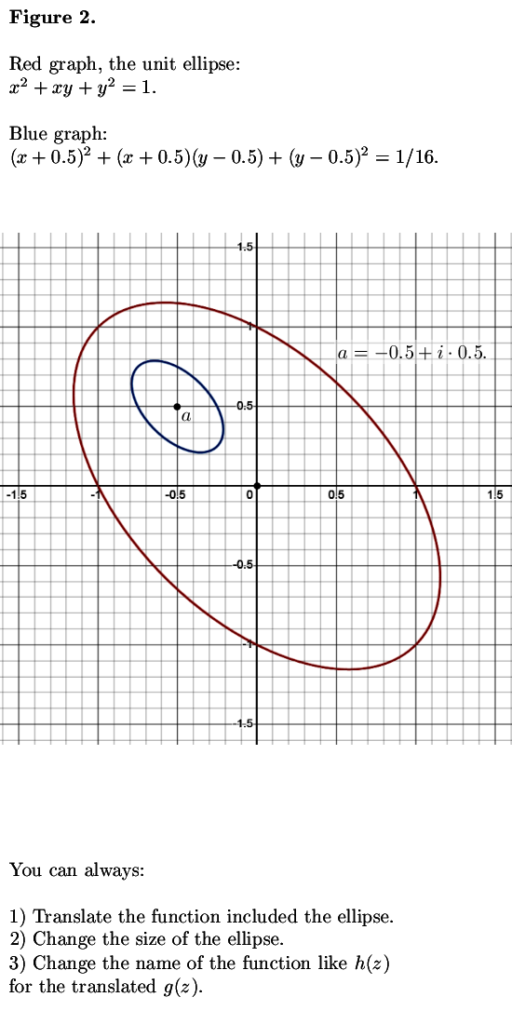
If you view the interger points of the plane equipped with the elliptic complex multiplication as prime numbers or composites, you have found a good basis to predict or calculate how much of such integer solutions there are. This problem is closely related to the number of integer points on a circle, I am sure you can find enough internet resources of that problem.
I decided to take a deeper look into this because of a video on the Eisenstein primes, those Eisenstein primes and integers look a lot like my own elliptic complex integers. But the Eisenstein numbers are defined on the standard complex plane while I modified the way the multiplication is done via a tiny change to i^2 = -1 + i. So that now ‘rules’ my plane with elliptic complex numbers and one of the nice properties is that i^3 = -1 while for that Eisenstein stuff you get +1. So the Eisenstein numbers are more a way of say the split complex numbers.
Lets start with the video that I considered to be remarkable good:

For me it was all brand new because to be honest I never ever studied the Gaussian integers and how that gives rise to a unique way of factorizing them. But now I had to solve the problem for my own 2D elliptic numbers I have to say that yes it is beautiful once you grasp what’s going on.

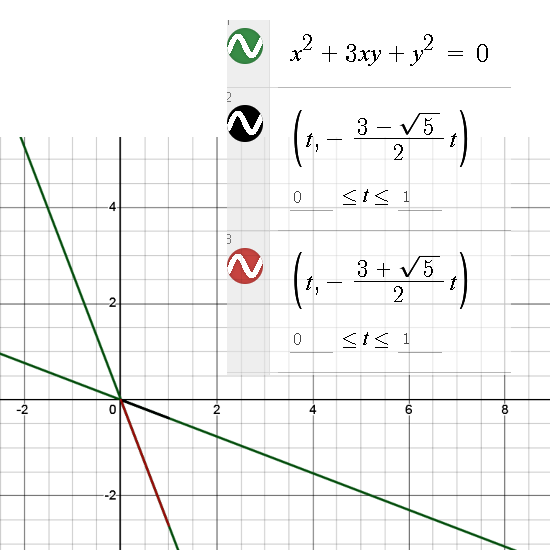
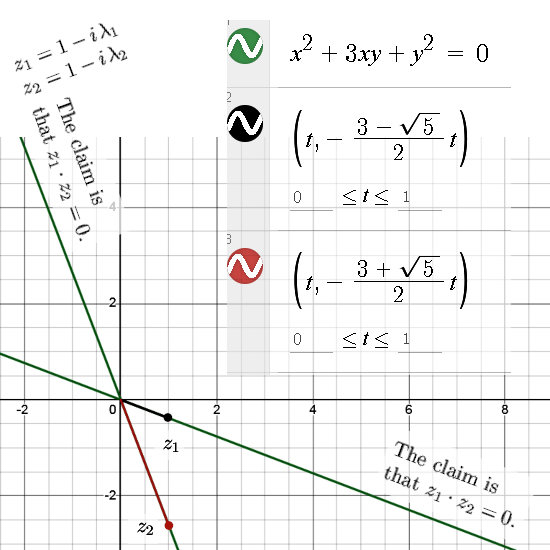
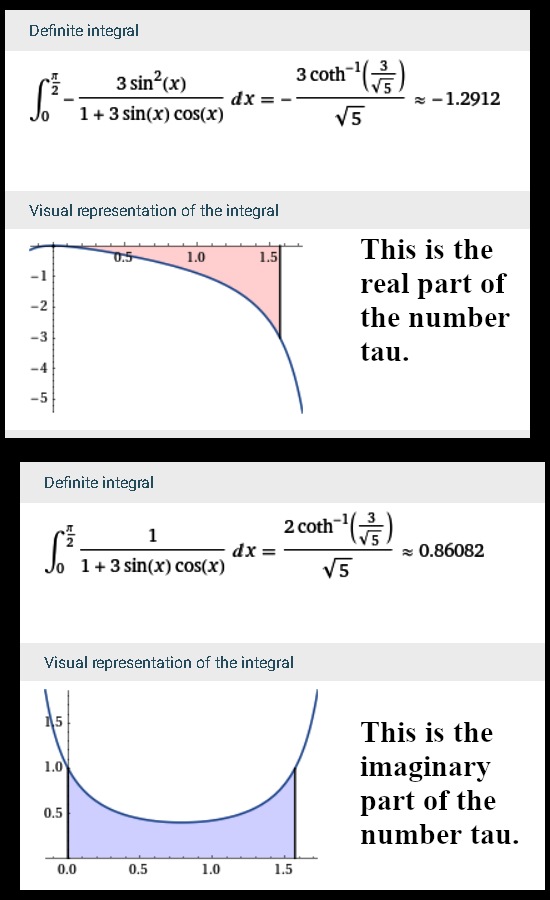
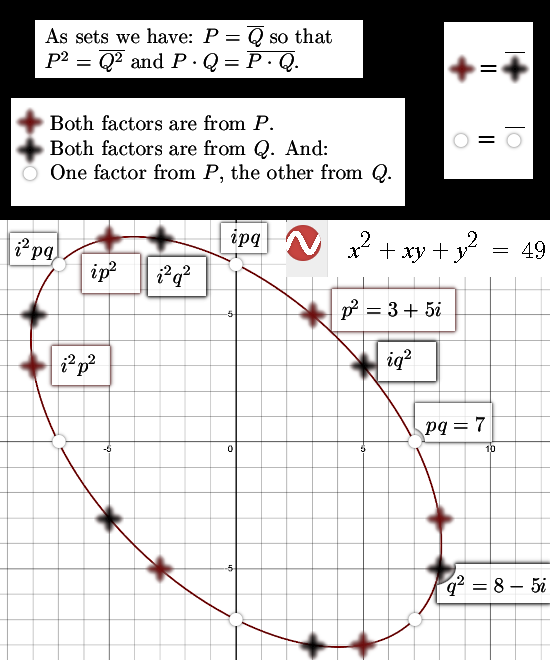
A well known fact from the Gaussian integers is that the number 5 is now no longer a prime number because it can be factored into 2 + i and 2 – i. On the complex elliptic numbers it is 7 that is the smallest integer to have that same fate as 5 on the Gaussian integers. This post is mostly about the two factors that factorize 7, I named them p and q and the interesting thing is they are each others conjugate.
But the number 3 is also no longer a prime so all in all for a person like me who dislikes algebra so often for so many years, it was all in all a nice patch of math to understand.

This post is 8 pictures long, each 550×1250 pixels and on top of that two extra figures are addes. So what more do you want? I kept the stuff as less technical as possible while hoping that if you want to dig a bit deeper you can do that for yourself now. So lets start the picture thing:

Figure 1: Seven is the smallest number that has two conjugate prime factors.
Figure 2: These are the 18 integer solutions to det(z) = 49.

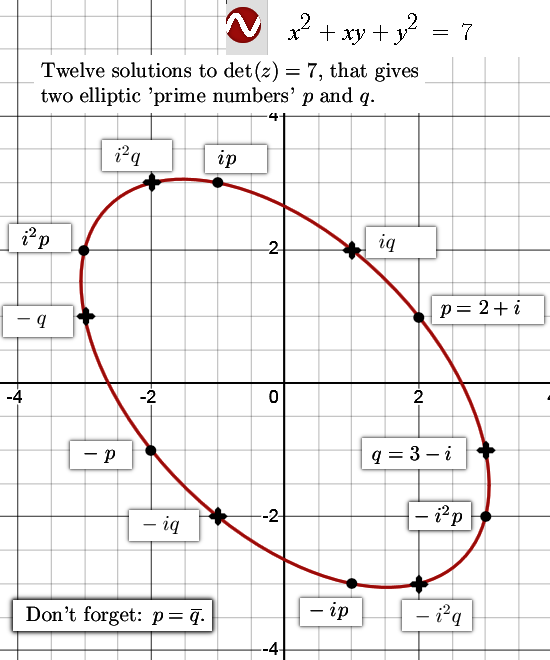
Here is a link to the free Wolfram webpage where you can check that indeed 1729 has 48 integer solutions because you can make 8 different factors with the prime numbers involved: https://www.wolframalpha.com/input?i=x%5E2+%2B+xy+%2B+y%5E2+%3D+172

Here’s the wiki: https://en.wikipedia.org/wiki/Unique_factorization_domain.
That was it for this post, thanks for your attention.

A Cauchy integral representation for the 2D elliptic complex numbers.

2D multiplications, Integration

This post is a bit deeper when it comes to the math side, I think you better understand it if you already know what such a Cauchy integral representation for the standard complex plane is. I remember a long long time ago when I myself did see this kind of representation for the first time, I was completely baffled by this. How can you come up with a crazy looking thing like this?
But if you look into the details it all makes sense and this representation is the basis for things like residu calculus that you can sometime use to crack an integral if all more easy approaches fail.
In most texts on the standard complex numbers (with standard I mean that the imaginary unit i behaves like i^2 = -1 whereas on my elliptical version the behavior is i^2 = -1 + i) it is first shown that you can take such integrals over arbitrary closed contours going counter clockwise. If the function you integrate has no poles on the interior of that contour, the integral is always zero.
I decided to skip all that although if you want, you can do that of course for yourself. I also skipped all standard proofs out there because I wanted to craft my own proof and therefore in this post we only integrate over the ellipses and nothing else.
Another thing to remark is that this is just a sketch of a proof, a more rigor approach would make the post only longer and longer and I think that people who are interested in math like this are perfectly capable of checking any details they think that are missing or swept under the carpet. For example I show in this post the important concept of ‘radial independence’ but I show that only for a very simple function g(z) = 1. It’s just a sketch and sometimes you have to fill in what is missing yourself. Sorry for being lazy but now already this post is 5 and a half pictures long so that’s long enough.

It also contains two extra figures and may be I will write a small appendix related to figure 1. But I haven’t done that yet so below is the stuff and I hope you like it.

Figure 1: The elliptic complex exponential and it’s coordinate functions.
Figure2: This is just some arbitrary point a and some arbitrary radius of 1/16.

Ok, all that is left is an appendix where I give a third parametrization of the elliptic complex exponential. It is just some leftover from some time ago when I wondered if the two coordinate functions might some some time lags of each other. And yes, they are. In the case of these elliptic complex numbers the time lag is one third of the period.

Before I end this post, why not place a link to all that official knowledge there is around the Cauchy integral representation there is. Here is a link:
https://en.wikipedia.org/wiki/Cauchy%27s_integral_formula

That was it for this post, as always thanks for your attention.


Eigenvalue functions for the elliptic complex plane.

2D multiplications

This is a very short post, in it I even joke this is done in “Tik Tok style”. It is about finding the eigenvalues for an arbitray elliptic complex number. Such numbers have matrix representations and as such they have also eigenvalues that live in the ordinary complex plane.
Here the elliptic plane is the same as we always studied the last couple of months, it is ruled by the imaginary unit i via i^2 = -1 + i. If you need the eigenvalues of such a number, instead of going through the calculation for eigenvalues every time, with the eigenvalue functions you just substitute it in and it spits out the two eigenvalues.
To be honest I did not explain in detail why it works, I hope it is rather obvious. Take for example two commuting (square) matrices A and B. They have the same eigen vectors (because they commute) and as such it is very easy to find the eigenvalues of any linear combination of A and B.

The post itself is only two pictures long and I included a third picture that I used on the other website. Beside a female robot the third picture contains another factorization of the equation of the ellipse that is the determinant of the matrix representations.
So this equation for the ellipse can be factored on the standard complex plane and also on the elliptic complex plane. The interesting detail is of course that on the elliptic complex plane you have integer coefficients while on the standard complex plane this is impossible.

Basically the eigenvalue funtions are both a map from the elliptic complex plane to the ordinary complex plane. If it was made by a professional math professor he or she would likely call it an isomorphism but I name them eigenvalue functions. In the past I also made them for the 3D complex and circular numbers and of course for the 4D complex numbers that were under study years ago.
Enough of the introdutionary talk, lets go:

There is a small ‘cut & paste’ error at the top of the next picture.

Now I left a lot of stuff out otherwise it would not be a Tik Tok short kind of math post. But you can also use the elliptic complex plane as your primary source of eigenvalues. For example at the other side of our galaxy there lives an alien race known as the Orcs. And for some kind of religious reason these Orcs just don’t want to use circles because as they all know circles are evil. But they found the elliptic complex plane and they use that for solving eigenvalue problems like eigenvalues from square matrices or even stuff that we humans know as the Hamiltonian energy operator. That should work just as good as we humans do in using the complex plane we have over here where the complex exponential is a circle.
So let us now look at the third picture that has both factorizations in it:

This cleary is not for math professors; they won’t understand this conjugate.

Let me leave it with that and as always thanks for your attention.

The cousin of the transponent.

2D multiplications, 3D complex numbers, Matrix representation

Likely in the year 1991 I had figured out that the conjugate of a 3D complex number could be found in the upper row of it’s matrix representation. As such the matrix representation of a conjugate 3D number was just the transpose of the original matrix representation. Just like we have for ordinary complex numbers from the complex plane. And this transpose detail also showed that if you take the conjugate twice you end where you started from. Math people would say if you do it twice, that is the identity operation.
But for the two 2D multiplications we have been looking at in the last couple of months, the method of taking the upper row as a conjugate did not work. I had to do a bit of rethinking and it was not that hard to find a better way of defining the conjugate that worked on all spaces under study since the year 1991. And that method is replace all imaginary units by their inverse.
As such we found the conjugate on 2D spaces like the elliptical and hyperbolic complex planes. And the product of a 2D complex number z with it’s conjugate nicely gives the determinant of the matrix representation. And if you look where this determinant equals one, that nicely gives the complex exponentials on these two spaces: an ellipse and a hyperbole.
Now when I was writing the last math post (that is two posts back because the previous post was about magnetism) I wondered what the matrix representation of the conjugate was on these two complex planes. It could not be the transpose because the conjugates were not the upper rows. And I was curious what it was, it it’s not the transpose what is it? It had to be something that if you do it twice, you do the identity operation…

All in all in this post the math is not very deep or complicated but you must know how te make the conjugate on say the elliptic complex plane. On this plane the imaginary unit i rules the multiplication by i ^2 = -1 + i. So you must be able to find the inverse of the imaginary unit i in order to craft the conjugate. On top of that you must be able to make a matrix representation of this particular conjugate. If you think you can do that or if you don’t do it yourself you will understand how it all works, this post will be an easy read for you.

It turns out that the matrices of the conjugate are not the transpose where you flip all entries of the matrix into the main diagonal. No, these matrix representation have all their entries mirrored in the center of the matrix or equivalently they have all their entries rotated by 180 degrees. That is the main result of this post.

So that’s why I named it the “Cousin of the transponent” although I have to admit that this is a lousy name just like the physics people have with naming the magnetic properties of the electron as “spin”. That’s just a stupid thing to do and that’s why we still don’t have quantum computers.

Enough intro talk done, the post is five pictures long and each picture is 550×1200 pixels. Have fun reading it.


That was it for this post, one more picture is left to see and that is how I showed it on the other website. Here it is:

Ok, this is really the end of this post. Thanks for your attention and may be see you in another post of this website upon complex numbers.

Another way of finding the direction of the number tau.

2D multiplications, 3D complex numbers, 4D complex numbers, Matrix representation

A bit like in the spirit of Sophus Lie lately I was thinking “Is there another way of finding those tangets at the number 1?”. To focus the mind, if you have an exponential circle or higher dimensional curve, the tangent at 1 is into the direction of the logarithm you want to find.
In the case of 2D and 3D numbers I always want to know the logarithm of imaginary units. A bit more advanced as what all started a long time ago: e^it = cos t + i sin t.
An important feature of those numbers tau that are the sought logs is that taking the conjugate always the negative returns. Just like the in the complex plane the conjugate of i is –i.

The idea is easy to understand: The proces of taking a conjugate of some number is also a linear transformation. These transformations have very simple matrices and there all you do is try to find the eigenvector that comes with eigenvalue -1.
The idea basically is that tau must like in the direction of that eigenvector.

That is what we are going to do in this post, I will give six examples of the matrices that represent the conjugation of a number. And we’ll look at the eigenvectors associated with eigenvalue -1.

At the end I give two examples for 4D numbers and on the one hand you see it is getten a bit more difficult over there. You can get multiple eigenvectors each having the eigenvalue -1. Here this is the case with the complex 4D numbers while their ‘split complex’ version or the circular 4D numbers have not.
Now all in all there are six examples in this post and each is a number set on it’s own. So you must understand them a little bit.
The 2D numbers we look at will be the standard complex plane we all know and love, the elliptic and hyperbolic variants from lately. After that the two main systems for 3D numbers, the complex and circular versions. At last the two 4D multiplications and how to take the conjugate on those spaces.

The post itself is seven pictures long and there are two additional pictures that proudly carry the names “Figure 1” and “Figure 2”. What more do you want? Ok, lets hang in the pictures:

The purple line segment points into the direction of tau.
That’s why 4D split complex numbers are just as boring as their 2D counter parts.

Years ago it dawned on me that the numbers tau in higher dimensional spaces always come in linear combinations of pairs of imaginary units. That clearly emerged from all those calculations I made as say the 7D circular numbers. At the time I never had a simple thing to explain why it always had to be this pair stuff.
So that is one of the reasons to post this simple eigen vector problem: Now I have a very simple so called eigen value problem and if the dimensions grow the solution always come in pairs…

That was it for this post, likely the next post is upon so called ‘frustrated’ magnetism because the lady in the video explains the importance of understand energy when it comes to magnetism. After that may be a new math post on matrix representations of the actual conjugates, so that’s very different from this post that is about the matrices from the process of taking a conjugate…
As always thanks for your attention.

A look at the set of non invertible hyperbolic 2D complex numbers.

2D multiplications, Last Fermat theorem

This is a horrible simple post, after all for the complex numbers ruled by i^2 = -1 + 3i all you have to do is look where the determinant of the matrix representaitons equals zero.
Well yes that is what we do, at present day there is that cute package or applet (in the past that was a so called computer program, why is all that kind of stuff an “applet” nowadays?) called DESMOS. With DESMOS the two lines that make up the set of non-invertibles is easy to graph.
These two lines are interesting because they are the asymptotes of all those hyperboles in this space, anyway those hyperboles that can be written as det(z) = constant. Furthermore the two lines where det(z) = 0 separate the parts of this complex plane where det(z) > 0 from the parts where det(z) < 0.

I took the opportunity to introduce a more comprehensive notation to denote such spaces of 2D complex and split complex numbers. I wrote it much more as a set like in set theory and it includes the ‘rule’ for the imaginary component.

For readers who are new to this website and don’t have a clue what ‘hyperbolic’ or ‘elliptical’ 2D complex numbers are, it is all basically rather simple:
These numbers are complex because i^2 = -1 + something, in the case of this post it is i^2 = -1 + 3i. These 2D complex numbers have matrix representations and the determinant of these matrices are constant along certain hyperboles. The case det(z) = 1 is very interesting for any of such a complex plane because that is a multiplicative group. Just like the unit circle in the standard or ordinary complex plane is a multiplicative group.

All in all this post has five pictures of size 550×1200 pixels and an additional two figures from graphs from the DESMOS applet.

For me it was funny to write some ‘high school math’ with just a few parabole kind of stuff in it. During the writing of this post I came across the idea of making a matrix representation of all that conjugating stuff, as such I found a beautiful but still extremely simple way to find the direction of the number tau in a particular space. The great thing is that this time it works in all dimensions so not only the 2D complex numbers but likely much much more.
Lets try to upload my post to the internet and may I thank you for your attention.