Yes yes I know we already calculated the number tau for this space equipped with a hyperbolic multiplication. (That was a few posts back using matrix diagonalization.) But I had a few reasons to write this anyway, one reason was just curiosity. I wanted to know how those integrals looked and since we had calculated the number tau anyway we did not need to solve these integrals with pencil and paper.
I also wanted you to show how you can write the product of such a complex number z against it’s conjugate. On the standard complex plane this defines a circle and on our hyperbolic space it is of course a hyperbole.
At last I wanted to pen down the formula for finding the inverse on this particular hyperbolic complex number space. It looks just like the way this is done on the ordinary complex plane with the exception that if you calculate it the conjugate is a bit different.
For me it is funny that we have exactly the same looking formula for the calculation of inverses. All in all it shows that the fixation the professional math professors have on all that “The norm of the product is the product of the norms” kind of stuff is only true because on the standard complex plane the determinant equals the square of the norm of a complex number
z. In our present case of hyperbolic complex numbers we devide the conjugate by the determinant and those determinant define hyperboles and not circles. So nothing of that “The norm of the product is the product of the norms” kind of stuff. The deeper underlying mechanism is just always the determinant of the matrix representation.

It has to be remarked however that the study of normed spaces is important in itself and also in practice: If you can find a good norm for some difficult problem like the successive aproximations in say differential equations and you can prove using that norm the stuff converges, that is BINGO of course. Yet a norm is only a tool and not all there is inside that strange space known as human math.

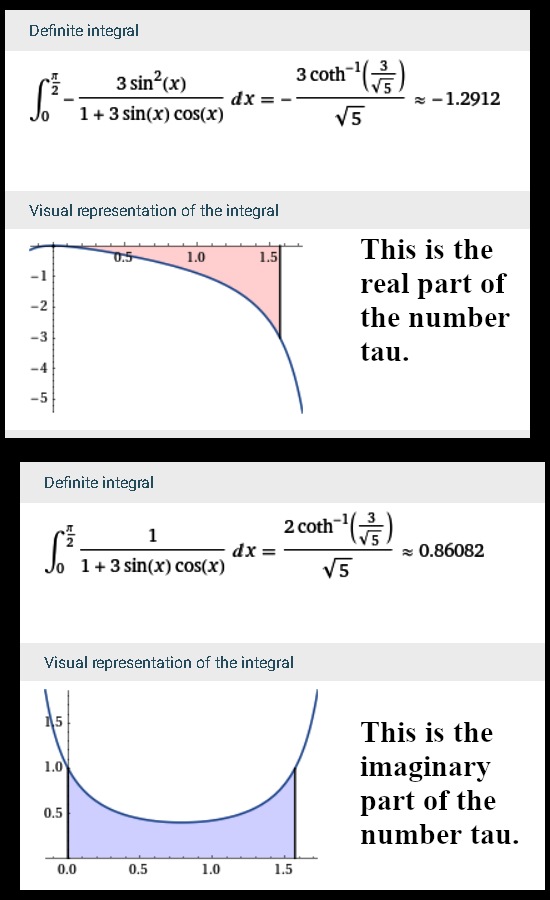
The post itself is 6 images long, in it I have two (pairs of) integrals going from 1 to i. The integrals are of course the inverse of a complex number because the derivative of the logarithm is the inverse and we want to know the log of i because by definition that is the number tau.

I included a so called Figure 1 that show the evaluation of these integrals by the Wolfram package for definite integrals, it’s a handy online tool in case you don’t want to evaluate your integrals with pencil and paper.
The last image is from the other website where once more I want to insult the math professors just a tiny tiny bit by using the standard formula of finding the inverso on the standard complex plane.
So all in all this post is 8 pictures long.

That was it more or less for this post, I hope you are a bit more confident by now that you can actually integrate spaces like this more or less just like you do in the standard complex plane. The last image is from the other website, it contains a female robot. Why there are female robots is unknow to me, after all with other tools you never have females like have you ever heard of a female screw driver or a female mobile phone?

Ok, that was it for this post. Thanks for your attention and just like the female robot look up into the light and start thinking about the wisdom behind “The norm of the product is the product of the norms”.