Monthly Archives: February 2023

Why could Hamilton not find the three dimensional complex numbers?

3D complex numbers, 4D complex numbers

This very short post was written because of a video from the video channel Kathy loves physics. It is one of those “Quaternions are fantastic” video’s. And Kathy just like a lot of other physics people think indeed that quaternions are fantastic. But you cannot differentiate or integrate on the quaternions so I guess this stronly limits it’s use in physics.
But quaternions are very handy in describing rotations in 3D space, I never studied the details but it was said that on the space shuttle it was used for nagvigation. And because of these rotation properties at present day they are used in the games industry.

Anyway in the video Kathy explains that Hamilton did try for a long time to find the three dimensional complex numbers. And he never succeeded in that. Of course I know this for decades right now but in the past I never looked into a tiny bit more detail in what Hamilton was actually doing.
And he was looking at complex numbers of the form X = x + yi + zj where the imaginary components both equal to minus one: i^2 = j^2 = -1.

If you check the easy calculations in this post for yourself, it is amazing how much it already looks like the stuff as found on the quaternions. As such it is all of a sudden much less a surprise that Hamilton found the quaternions. As a matter of fact it was only waiting until he would stumble across them. But at the time the concept of a four dimensional space was something that made you look like a crazy lunatic, there were even vector wars and lots of crazy emotional stuff.

At present day it is accepted that 3D complex numbers do not exist, in my experience the professional math community is still emotionally laden but now into the direction of total neglect. Stupid shallow thought like “If Hamilton could not find them, they likely don’t exist”.

Back in the 19-th century they were always looking for an extenstion of the complex plane to three dimensional space. Of course they failed in that attempt because it is a fact of math life that you cannot solve the equation X^2 = -1 on the space of 3D complex (and also circular) numbers.

The content of this post is just two pictures, after that two more pictures as I used them on the other website and after that you can finally dive into the Video from Kathy. If you are interested in physics and also the history of physics, Kathy her channel is a thing you should take a look at if you’ve never seen it. Here we go:

YES, that is what he should have done. Hamilton tried for about one decade to find the numbers that form the title of this very website, so may be he tried this kind of approach. I don’t know, but the 3D complex numbers are not some extension of the complex plane because 2 is not a divisor of 3. You know that prime number stuff is going on here.
But the math professors are not interested in that kind of stuff.

Here is how I used it on the other website:

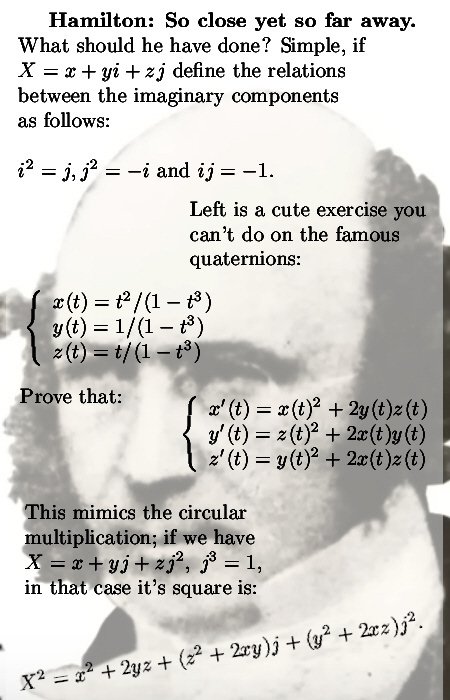
As you see in the above picture I was already working on the previous post because if you differentiate the three functions that mimics the 3D circular multiplication. You can also mimic the multiplication on the complex plane, that is in the next picture:

At last you can view the famous video of Kathy! It’s only 30 minutes or so but if you see too many so called TIKTOK videos that is infinitely long: Wow 30 minutes long looking at just one video?

End of this post, likely the next post is about 4D complex numbers.

Solving the ‘Speed = The Square’ equation on four different spaces.

3D complex numbers, Matrix representation, Uncategorized

With ‘speed = square’ I simply mean that the speed is a vector made up of the square of where you are. The four spaces are:
1) The real line,
2) The complex plane (2D complex numbers),
3) The 3D circular numbers and
4) The 3D complex numbers.

I will write the solutions always as dependend on time, so on the real line a solution is written as x(t), on the complex plane as z(t) and on both 3D number spaces as X(t). And because it looks rather compact I also use the Newtonian dot notation for the derivative with respect to time. It has to be remarked that Newton often used this notation for natural objects with some kind of speed (didn’t he name it flux or so?).
Anyway this post has nothing to do with physics, here we just perform an interesting mathematical ecercise: We look at what happens when points always have a speed that is the square of their position.

On every space I give only one solution, that is a curve with a specific initital value, mostly the first imaginary component on that space. Of course on the real line the initial condition must be a real number because it lacks imaginary stuff.

If you go through the seven pictures of this post, ask in the back of your mind question as why is this all working? Well that is because the time domains we are using are made of real numbers and, that is important, the real line is also a part of the complex and circular number systems.
The other way you can argue that the geometric series stuff we use can also be extended from the real line to the three other spaces. To be precise: we don’t use the geometric series but the fractional function that represents it.

Ok, lets go to the seven pictures:

That Newton dot notation just looks so cute…
The words ‘Analytic continuation’ are not completely correct…

Remark: This post is not deep mathematics or so. We start every time with a function we know that if you differentiate it you will get the square. After that we look at it’s coordinate functions and shout in bewilderment: Wow that gives the square, it is a God given miracle!

No these are not God given miracles but I did an internet search on the next phrase of Latex code: \dot{z} = z^2. To my surprise nothing of interest popped up in the Google search results. So I wonder if this is just one more case of low hanging math fruits that are not plucked by math professors? Who knows?

End of this post, thanks for your attention.