Monthly Archives: March 2021

Side remarks on the Frey elliptic curve.

Last Fermat theorem

Since this is the post number six on the Fermat stuff already, I decided to create a new category for this kind of math. It is no secret my knowledge of algebra is rather rudimentary, a lot of things in algebra are things I do not like to study or think about. I always had trouble learning algebra, often those people come up with say 15 definitions of algebra objects but all those definitions have the weight of a fly and rather soon I am lost in the forest. I much more prefer more heavy definitions of math objects (like the Cauchy-Riemann equations) and not stuff that is a semi-simple defined on a semi-simple kind of curve…
So I do not know much about number theory, a few days ago I downloaded the entire proof of Andrew Wiles where he proves that the last theorem of Fermat is actually true. Well already in the very first line I get lost; and in that proof you have all that Galois stuff so I think that I skip that entire proof for the time being.
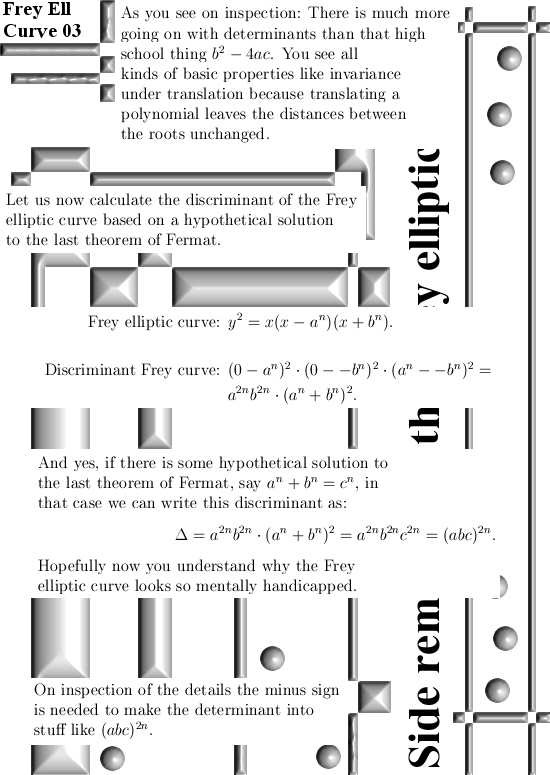
A lot of things are weird in number theory. For example that Frey elliptic curve is based on a hypothetical solution to the Fermat equation a^n + b^n = c^n. If you interchange a and b in the Fermat thing, every thing stays the same. But you get a different elliptic curve if you interchange a and b in that Frey ellipic curve. So I just had no clue; wtf is going on here? Luckily I found a video of Gerhard Frey explaining a bit about what and why and the elliptic curve he defined is done in that way so that the discriminant can be simplified using that theoretical solution to the last Fermat theorem. So it is not crazy but it has it’s own logic, yet search for yourself: how many texts are there that speak about this Frey elliptic curve and actually tell you this? Most math writers simply repeat the (old) knowledge and are bad at explaining why stuff is such and so.

I always work alone, actually it is not work but an important hobby, and because I have to figure out every thing alone I have no access to people with a lot of knowledge on the details & the broader lines of some kind of math theory. Because I work alone this often takes more time. Yet on the universities where the people are supposed to work together they have never found 3D complex numbers or counter examples to the last Fermat theorem. In other sciences like physics it also goes like crazy if you read what they made of electron spin in 100 years of time. So working together is not a guarantee of speeding things up. On the contrary if after a full century you still think that, for example, the electrons is a magnetic dipole you are crazy to the bone.

This post is a short one, only four pictures long. I nicely work out what that discriminant is supposed to be. Likely people like Andrew Wiles and Gerhard Frey have never seen counter examples to the last theorem of Fermat, so why not at the end of my post take a look at what happens in that case? Well it does not look very promising for the collective of overpaid math professors; such a determinant of the Frey elliptic curve is always zero… Anyway on all spaces I found where we have counter examples to the last Fermat theorem, such a discriminant is always zero.
And that is regardless of the last Fermat theorem counter example being true or false; sorry Gerhard Frey I don’t think this approach will bring any fruits at all…
Well here are the four pictures, all of the standard size of 550×775 pixels.

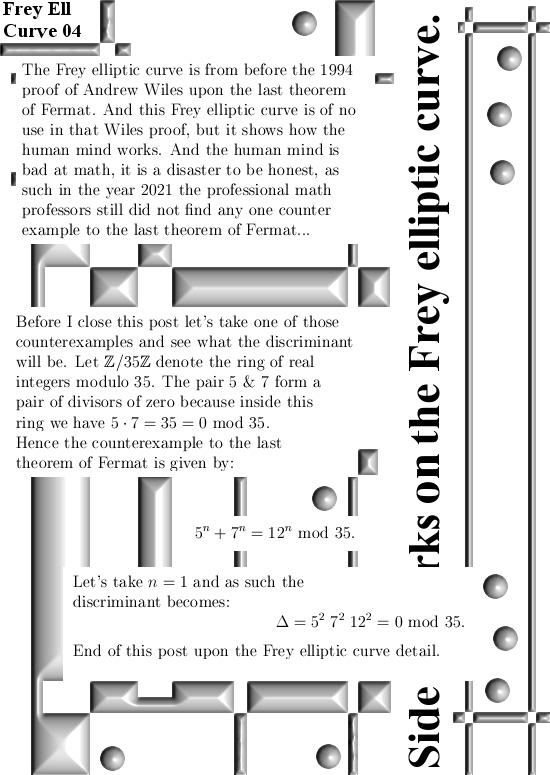
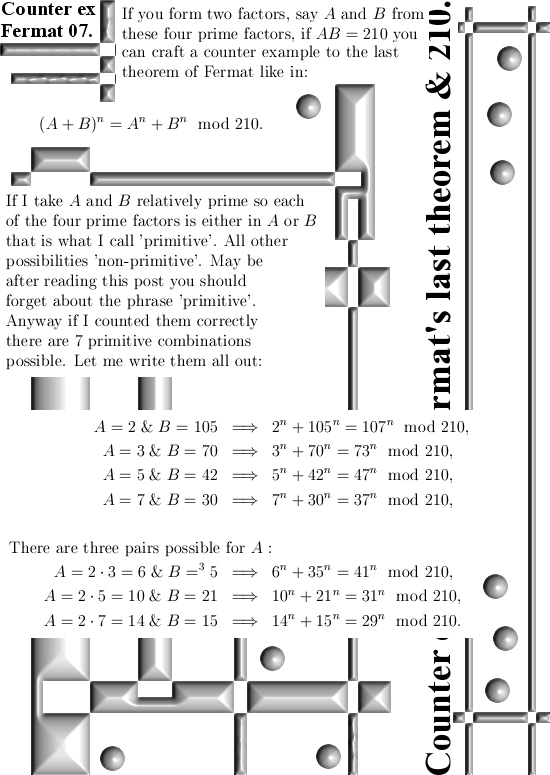
The only reason I wrote six posts on the Fermat stuff is that those counter examples like 5^n + 7^n = 12^n modulo 35 are too cute to ignore.
End of this post, thanks for your attention.

Counter examples to the last theorem of Fermat using the number 210.

Last Fermat theorem, Uncategorized

Ok ok one more post upon the easy to find counter examples to the last theorem of Fermat. In this post we will take a look at the real integers modulo 15 and modulo 210. It still amazes me how easy it is to find counter examples to the last Fermat theorem using the integers modulo n where n has at least two prime factors. From my own education I remember that the integers modulo n are studied in math mostly via additive groups and multiplicative groups. For some strange reason it is not commonly studied via rings where you have the benefit of addition and multiplication inside one simple to understand structure of numbers… Inside professional math there is always that tendency to study fields only, of course there a legitimate reasons for that like it makes math life often more simple. But rings are not fields, rings allow for non zero numbers that are non-invertible anyway. As such you can always find plenty of pairs of so called ‘divisors of zero’ and once you have stuff like that it is always a piece of cake to find counter examples to the last theorem of Fermat.

Yet I tried a few times to find some counter examples on the internet but all I got was boatload after boatload of total nonsense like the weird stuff paraded in the previous post. Could it be that math professors tried to find counter examples to the last theorem of Fermat while they never dipped into the power of the divisors of zero? That’s crazy because the Fermat theorem was open for about 350 years. I think many people have found the easy to understand results in this post before I did but if they tried to get the stuff out they were blocked by the scientists of those days and as such in the year 2021 it is hard to find something back.

Compare it to electron spin; it is hard to swallow that I am the very first person in history that claims electrons cannot be magnetic dipoles because it is just not logical for hundreds of reasons. Yet in the daily practice of how science is done at the universities, it is a no show that electrons are magnetic monopoles. What happened to all those other persons that understood that electrons cannot be magnetic dipoles? Well at least they got neglected and university life just went on with electrons being a magnetic dipole because ‘we are so smart’ and ‘the standard model explains almost everything’. And more of that nonsense…

This post is 8 pictures long, all of the usual size of 550X775 pixels.
Since it is about counter examples to the last Fermat theorem I expect it will not make much headlines in the news for another 3500 years.
After all the only thing university people are good at is being incompetent…;)
Here we go:

At last I found a more or less readable article about near misses of the last Fermat theorem. It was found inside old work from Ramanujan so that is always interesting. Most of the time when I looked for counter example to the last Fermat theorem I only find piles of garbage but this time I tried it with Duckduckgo and something readable comes floating up:
Ramanujan surprises again.
https://plus.maths.org/content/ramanujan

Ok that was it for this post. Thanks for your attention.

Why can’t I find counter examples to Fermat’s last theorem on the internet?

3D complex numbers, Last Fermat theorem, Uncategorized

After a few weeks it is finally dawning on me that it might very well be possible that the professional math people just do not have a clue about how easy it is to find counter examples to the FLT. (FLT = Fermat’s Last Theorem.) That is hard to digest because it is so utterly simple to do and understand on those rings of integers modulo n.
But I did not search long and deep and I skipped places like the preprint archive and only used a bit of the Google thing. And if you use the Google thing of course you get more results from extravert people. That skews the results of course because for extraverts talking is much more important compared to the content of what you are talking or communicating. That is the problem with extraverts; they might be highly social but they pay a severe price for that: their thinking will always be shallow and never some stuff deeply thought through…

As far as I know rings of the integers modulo n are not studied very much. Of course the additive groups modulo n are studied and the multiplicative groups modulo n are studied but when it comes to rings all of a sudden it is silent always everywhere. And now I am looking at it myself I am surprised how much similarity there is between those kind of rings and the 3D complex & circular numbers. Of course they are very different objects of study but you can all chop them in two parts: The numbers that are invertible versus the set of non-invertibles. For example in the ring of integers modulo 15 the prime factors of 15 are 3 and 5. And those prime factors are the non-invertibles inside this ring. This has all kinds of interesting math results, for example take the (exponential) orbit of 3. That is the sequence of powers of 3 like in: 3, 3^2 = 9, 3^3 = 27 = 12 (mod 15), 3^4 = 36 = 6 (mod 15) and 3^5 = 18 = 3. As you see this orbit avoids the number 1 because if it would pass through 1 you would have found an inverse of 3 inside our ring and that is not possible because 3 is a non invertible number…

Likely my next post will be about such stuff, I am still a bit hesitant about it because it is all so utterly simple but you must never underestimate how dumb the overpaid math professors can be: Just neglecting rings modulo n could very well be a common thing over there while in the meantime they try to act as a high IQ person by stating ‘We are doing the Langlands program’ & and more of that advanced blah blah blah.
Anyway it is getting late at night so from all that nonsense weird stuff you can find on Google by searching for counter examples to the last theorem of Fermat I crafted 3 pictures. Here is the first one:

I found this retarded question on quora. For me it is hard to process what the person asking this question was actually thinking. Why would the 2.999…. be important? What is this person thinking? Does he have integer solutions to say 2.9 and 2.99 and is this person wondering what would happen if you apply those integer solutions to 2.99999999…..???????

It is retarded, or shallow, on all levels possible. So to honor the math skills of the average human let’s make a new picture of this nonsense:

We will never be intimidated by the stupidity of such questions and simply observe these are our fellow human beings. And if ok, if you are a human being running into tons of problems, in the end you can always wonder ‘Am I a problem myself because I am so stupid?’

If you have figured out that question, you are getting more solid & you look more like a little cube:

I want to end this post on a positive note: Once you understand how stupid humans are you must not view that as a negative. On the contrary, that shows there is room for improvement.