Monthly Archives: March 2018

What is the inverse Pythagoras theorem?

Pythagoras stuff

It is already late in the evening, actually it is past midnight so I will keep the text of this post short. It was a nice day today and this evening I brewed the 23-th batch of a beer known as ‘Spin half beer’. (I name it that way because it contains only half of the dark malts I use in the beer known as dark matter…;) so it has nothing to do with electrons).

This is a very basic post about some ‘inverse Pythagoras theorem’ as came flying by in some math video. I was rather surprised that I have not seen it before but there are so many theorems out there using that old fashioned Euclidian geometry that I might have forgetten all about it.

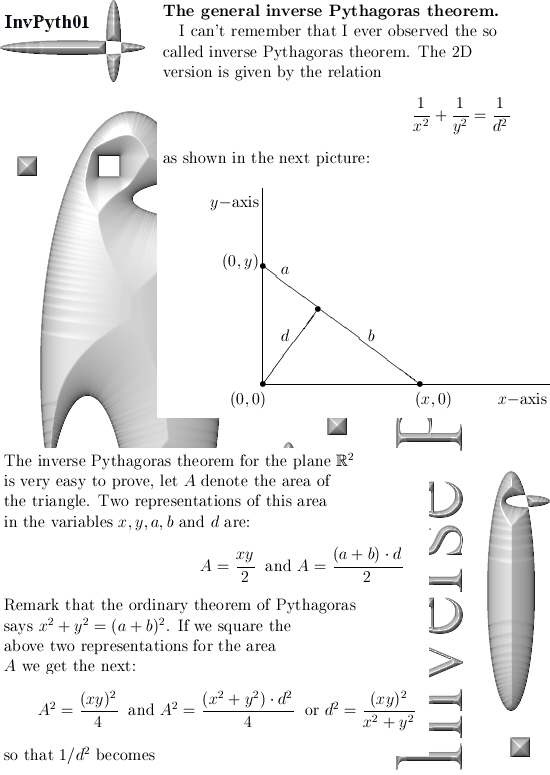
Within 10 minutes I had a good proof for the 2D version of this ‘inverse Pythagoras theorem’. You can find it in the first picture below.

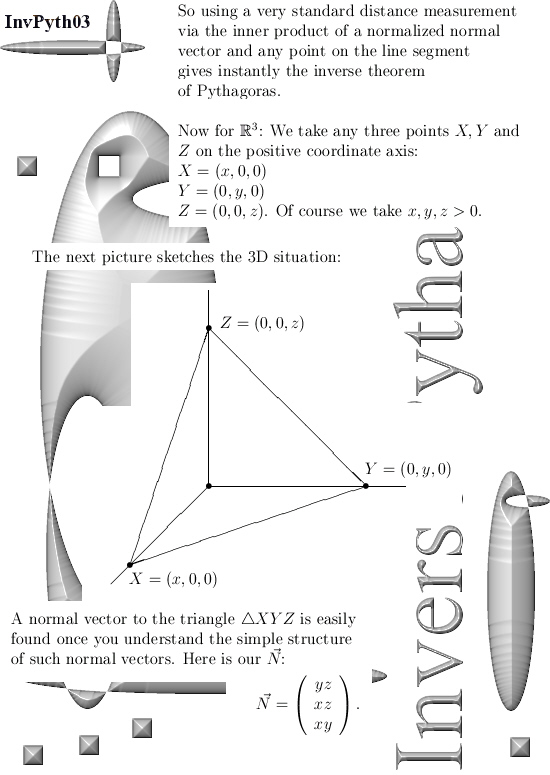
One day later when I was riding a bit around I tried to find the higher dimensional analog of that easy to understand 2D statement or theorem. And as such it crossed my mind the important role a distance number d played in my proof for the general theorem of Pythagoras that acts on simplexes that are the higer dimensional analog of 2D triangles.

Coming home it was easy to write out the details, but for me it was all so simple that does this stuff deserve the title ‘theorem’? Well make up your own mind about that, but if it is not a real complicated theorem it is still a nice and cute result…

This post is six pictures long (all 550×775 pixels beside the last one that needed a bit expansion because the math did not fit properly so that one is 600×775 pixels).

At times it might look difficult but this is only because it is in a general setting when it comes to the number of dimensions, the basic idea’s are all simple things like taking an inner product with a normalized normal vector.

Here are the six pictures:

That is a cute result but for me the normal vector is just as cute but only a bit harder to write out because that part deals with general setting where the dimension n is not fixed.

For the time being is this the end of this post. See you around my dear reader.

__________

Addendum added on 30 March 2018: In the previous post I forgot to place a link to the proof of the general theorem of Pythagoras as I crafted it once a long time ago.

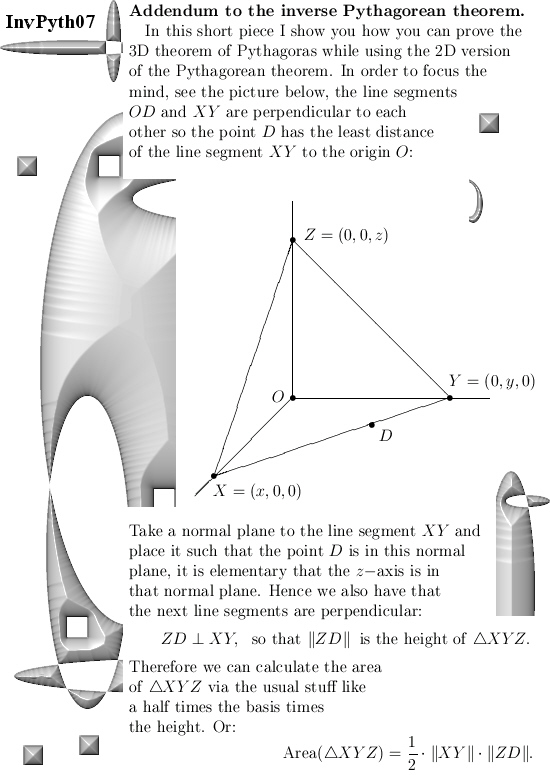
Before this link I would like to show you once more how to prove the general theorem of Pythagoras for the 3D case using only the 2D theorem.

After all, that is the first basic step in my proof for the general theorem of Pythagoras…

Here are the two addendum pictures outlining how this basic step from the two dimensional plane to the 3D space goes:

Here is the link to the proof of the general theorem of Pythagoras:

The general theorem of Pythagoras (second and final post).

The general theorem of Pythagoras (second and final post).

Ok that was it, till updates.

A new page on magnetics covering this year 2018.

Magnetism

After a little bit of thinking I decided to open another page on magnetic, mostly the tiny fact that electrons carry magnetic charge and are not magnetic dipoles, covering stuff as it is found in the year 2018.
Of course I will not push that idea for an infinite amount of time but this is about year number four and I still like it to look into the details of all things wrong with the official version of electron spin.
Likely this year will be as the previous years; total 100% silence from all physics professors, you can view that kind of behavior as a combination of being stupid and coward at the same time. This is known as a super position of cowardice and stupidity…
Also this year I will never ever try to attempt to write an official publication on the subject of electron spin, I still estimate the likelihood of rejection above 90% and on top of that I do not like it to be judged by some coward dumb ass.
No, the year 2018 is just another year of strong separation between me and all those university people.
__________
After having said that, here is the link to the new page three:

http://kinkytshirts.nl/rootdirectory/just_some_math/monopole_magnetic_stuff03.htm

This year I posted four more reasons as why electrons cannot have magnetic dipole properties of their own, basically most stuff observed like the electron pair in chemical bonding is not based on two magnetic dipoles doing ‘mysterious stuff’ but the pair is a sole reflection of the fact the pair has opposite magnetic charges.

Here is a screen shot from where I am now:

A very short description of the content of the four new posted reasons:

Reason 53: It was observed that in the IBM attempts to craft so called magnetic racetrack memory, the domain walls could not be moved by magnetic fields in those nano structures. Very boldly I simply claimed that in all metals with magnetic domains, the domain walls contain (much) more electron pairs…
This was very bold but if you want to shoot my theory out of the sky, the professional professors have to prove that the magnetic properties of the unpaired electron are more or less the same as the electron pair while at the same time upholding the Gauss law for magnetism (no magnetic charges do exist).

Reason 54: The circular magnetic field around circular (copper) wires when they transport electrical current. In my view, dependent on the magnetic charge of the individual electrons they will spiral at the surface of the wire into two different kind of spirals.

Reason 55: If what the video says is true and this is how the electron spin valve works, that is one more contribution to the simple fact electrons carry magnetic charge. It all boils down to the idea that opposite charges attrack while like charges repel.
That is the way such spin valves work.

Reason 56: After watching a lot of so called ‘spin torque transfer’ video’s I was so completely fed up with these people who only do theoretical blah blah blah but never ever in their lives as perfumed princes touch things like a screwdriver, I decided to do a simple experiment that debunkes a lot of that theoretical ‘spin torque transfer’.

Here is picture number two of my very simple experiment that shows there is no spin torque tranfer observed in a time frame of about 25 hours:

It is not observed: The strongest magnets possible in this year against the weakest macroscopic magnet still in my possesion, no spin torque transfer observed…..

__________

Ok, end of this post. Thanks for your attention.