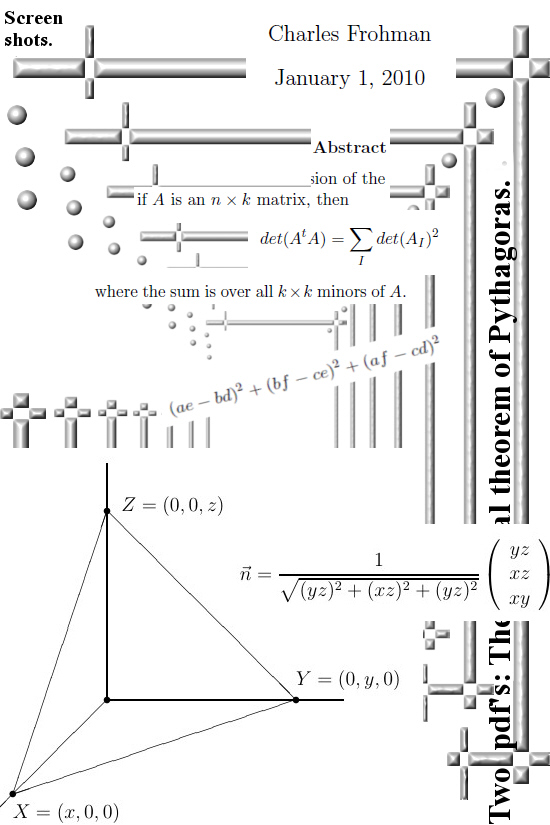
A few months back I found a very good text on more general versions of the good old Pythagorean theorem. Since in the beginning of this text the author Charles Frohman did the same easy to understand calculations as I did a long time ago I more or less trust the entire document. But I did not check the end with those exterior calculations, I don’t know why but I dislike stuff like the wedge product.
The second pdf is from myself, likely I wrote it in 2012 because a proof of a more general version of the theorem of Pythagoras was the first math text I wrote again after many years. After that at the end of 2012 I began my investigations into the three dimensional complex numbers again and as such this website was needed in 2015.
Anyway I selected 3 details from these two pdf’s that I consider beautiful math ideas where of course I skip a definition of what ‘beautiful’ is. After all the property ‘mathematically beautiful’ is not a mathematical object but more a feeling in your brain.
Let me start with four pictures where I look into those 3 selected details, after that I will hang the two pdf texts into this post.

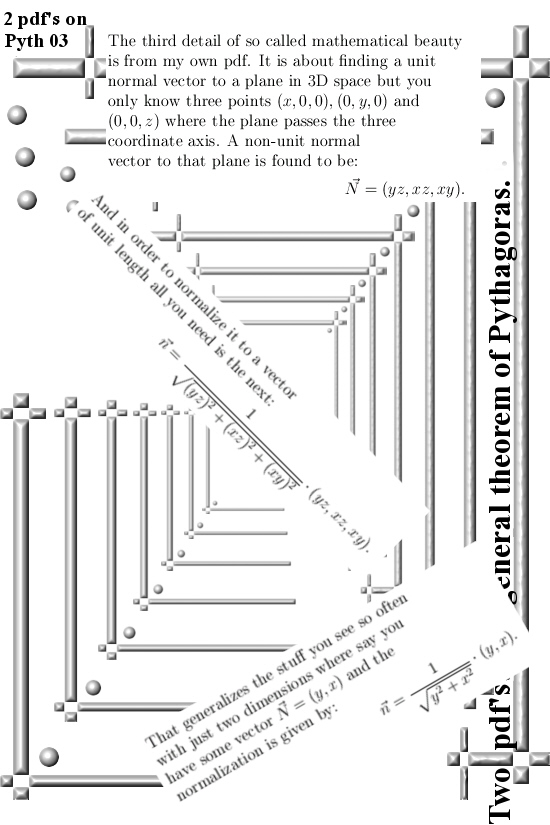
The first pdf is from Charles Frohman. May be you must download it first before you can read it, I should gain more experience with this because the pdf format is such a hyper modern development…;)
The first text is from 2010:
At last my old text from 2012:
(Later I saw there were some old notes at the end of my old pdf, you can neglect that, it has nothing to do with the Pythagoras stuff.)
There is little use in comparing these texts, I only wanted to make a proof that uses natural induction so I could prove the theorem in all dimensions given the fact we have a proof (many proofs infact) for the theorem of Pythagoras with a rectangular triangle. Charles his text is more broader and the main piece is the proof for that determinant version of the theorem of Pythagoras.
At last a remark about the second detail of mathematical beauty: Charles gave the example of a parallellogram where the square of the area equals the sum of squares of the three projections on the three coordinate planes. I think you can take any shape, a square of a circle it does not matter. It only matters it is a flat thing in 3D space. After I found that within the hour I had a proof for the general setting of this problem in higher dimensional real space, may be this is for some future post.
For the time being let us split and go our own ways & thanks for the attention of reading this.