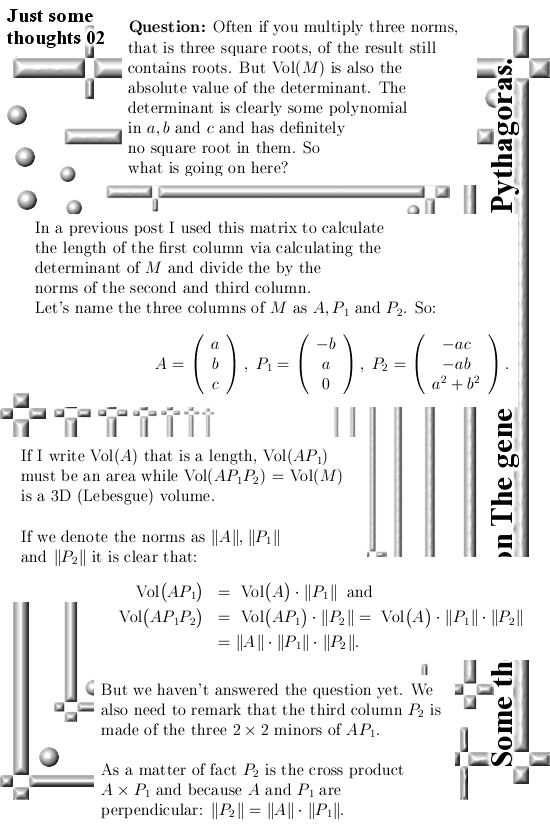
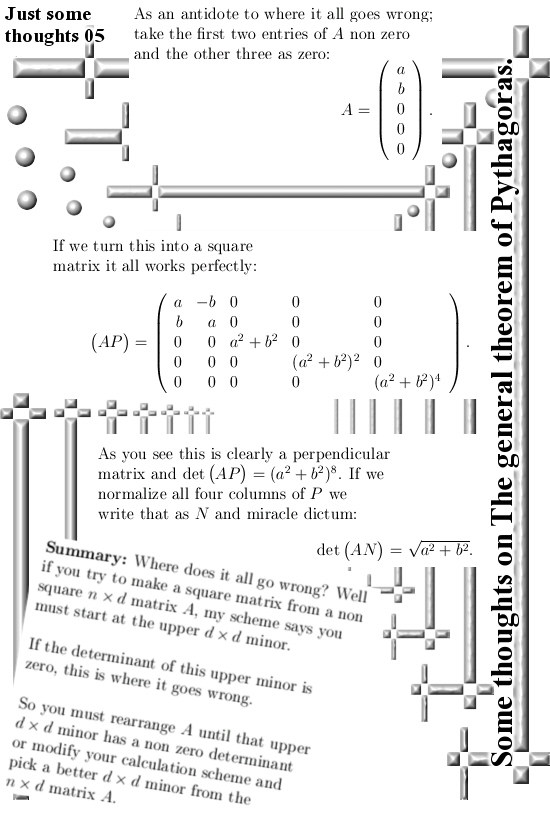
I remember that in the past a few times I tried to write determinants of say a nxn matrix in determinants of blocks of that matrix. It always failed but now I understand the way the matrix version of the theorem of Pythagoras goes, all of a sudden it is a piece of cake.
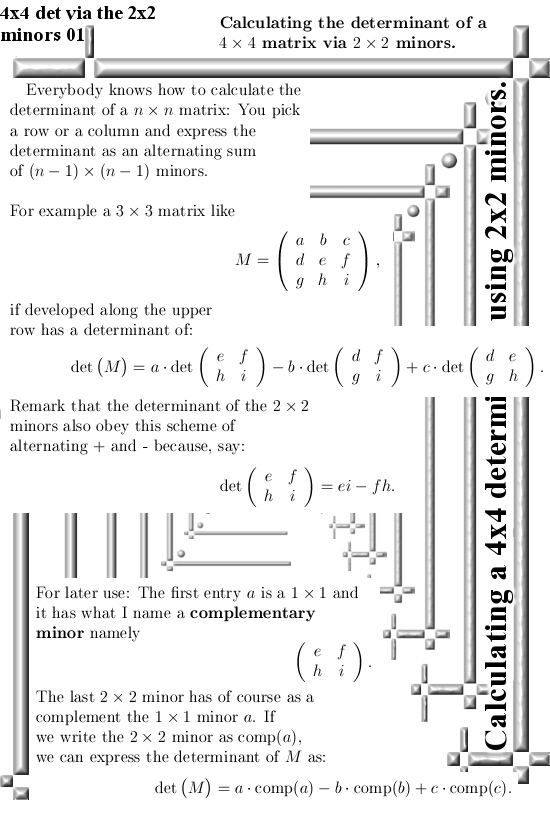
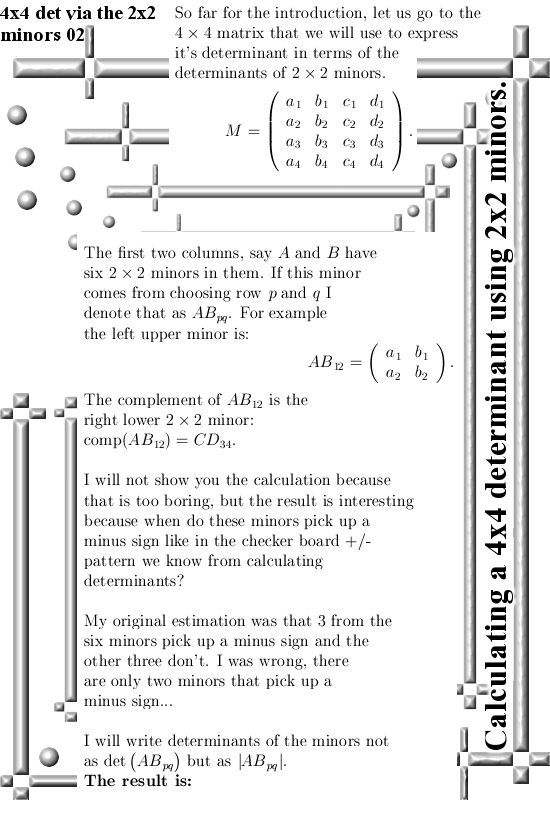
In this post I only give an example of a 4×4 matrix. If you take the first two columns of such a matrix, say AB, this is now a 4×2 matrix with six 2×2 minors in it.
If we name the last two columns as CD, for every 2×2 minor in AB there is a corresponding complementary 2×2 minor in CD. For example if we pick the left upper 2×2 minor in our matrix ABCD, it’s complement is the right lower 2×2 minor at the bottom of CD.
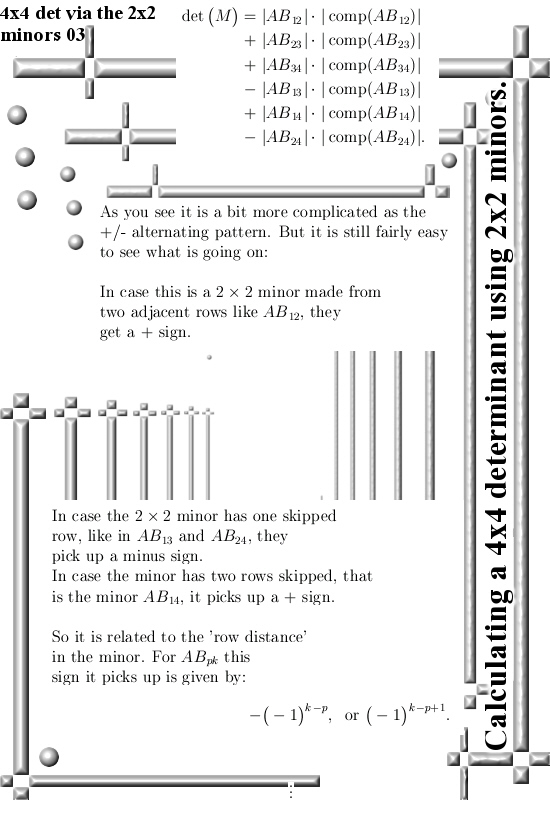
If you take the determinants of those minors and multiply them against the determinants of their complements, add it all up with a suitable +/- pattern and voila: that must be the determinant of the whole 4×4 matrix.

This method could more or less easily expanded to larger matrices, but I think it is hard to prove the +/- pattern you need for the minors of larger matrices. Because I am such a dumb person I expected that half of my six 2×2 minors pick up a minus sign and the other half a plus sign. Just like you have when you develop a 4×4 determinant along a row or column of that matix. I was wrong, it is a bit more subtle once more confirming I am a very very dumb person.

I skipped giving you the alternative way of calculating determinants: The determinant is also the sum of so called signed permutations on the indices of their entries. If you have never seen that I advice you to look it up on the internet.

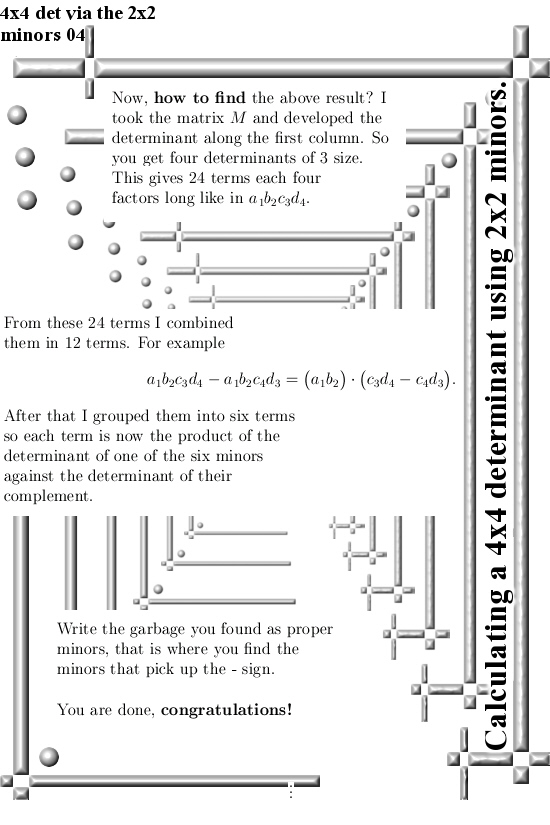
Because I skipped excisting knowledge widely available already, I was able to do the calculation in just four images! So it is a short post. Ok ok I also left out how I did it in detail because writing out a 4×4 determinant already has 24 terms with each four factors. That’s why it is only four pictures long in this post…

If you want you can also use that expression as the determinant as a sum of signed permutations. It is a very cute formula. Wiki title:
Leibniz formula for determinants.
And a four minute video, it starts a bit slow but the guy manages to put in most of the important details in just four minutes:

Ok, that was it for this post. I filed it under the category ‘Pythagoras stuff’ because I tried similar stuff in the past but only with the knowledge into the matrix version of the Pythagoras theorem, it all becomes a bit more easy to do.

Thanks for your attention.

To be honest this post is not carefully thought through. I felt like starting to write and at first I wanted to write it more into the direction of a proof based on the volumes of the parallelepiped and it’s expansion columns. But then I realized that my cute calculating scheme of turning a nxd matrix A into a square nxn matrix AP could go wrong. So I wanted to address that detail too but I hadn’t thought it out enough.

The answer to why it can go wrong is rather beautiful: Take any nxd matrix (of course the number of columns cannot exceed n because that is not a proper d-dimensional parallelepiped) say a 10×3 matrix. The three columns span a parallelepiped in 10-dimensional real space.
The ‘smallest’ parallelepiped that still has a three dimensional volume is one of the many minors possible in the 10×3 matrix. So with ‘smallest’ I mean the parallelepiped that uses the least number of coordinates in our 10-dimensional space.
Now in my calculating scheme, an algorithm if you want, I said you to start at the top of the matrix A and add more and more columns. But if A is made of just one 3×3 minor, say at the bottom of A, it is crystal clear my calculating scheme goes wrong because it now produces only zero columns.

And if that happens, when in the end you take the determinant of the square matix AP you get zero and of course that is wrong. These are exceptional cases, but it has to be addressed.


Of course there is no important reason for the calculation scheme to start at the top of the matrix, just start at the position of the lone 3×3 minor. In general: If you start with a nxd matrix, ensure your first expansion column is not a zero column. After that the next expansions all should go fine.

This post is five pictures long. If you haven’t mastered the calculation scheme of how to turn a non-square matrix into a square matrix you must first look up previous posts until you have a more or less clear mental picture of what is going on with this.

Ok, that was it for this post on the highly beautiful calculation scheme for the volumes of parallelepipeda in higher dimensions.