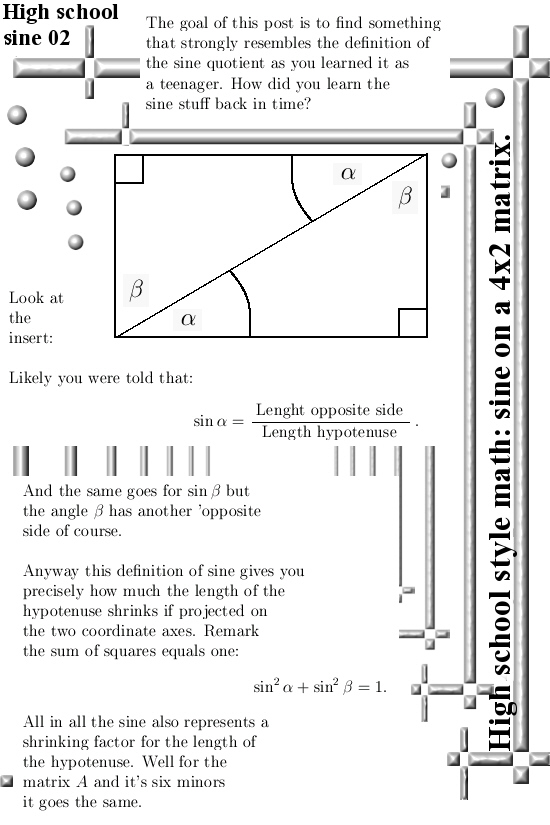
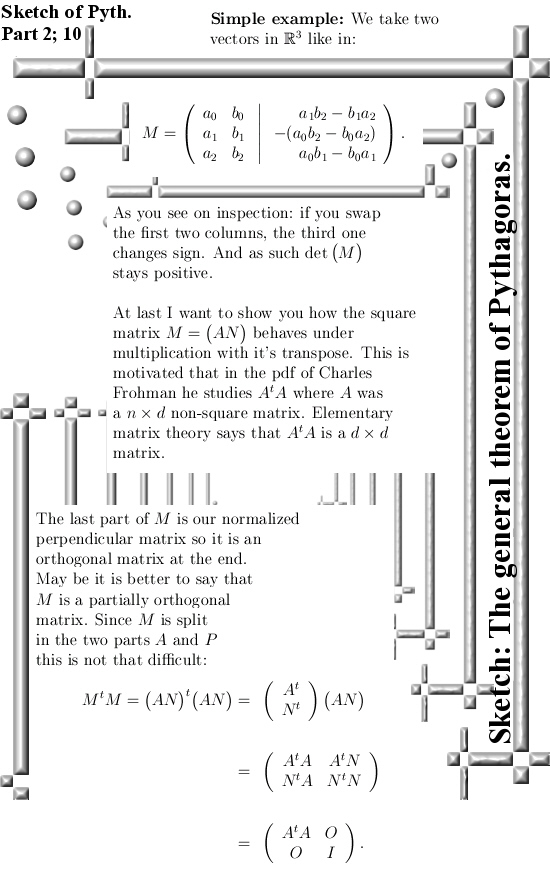
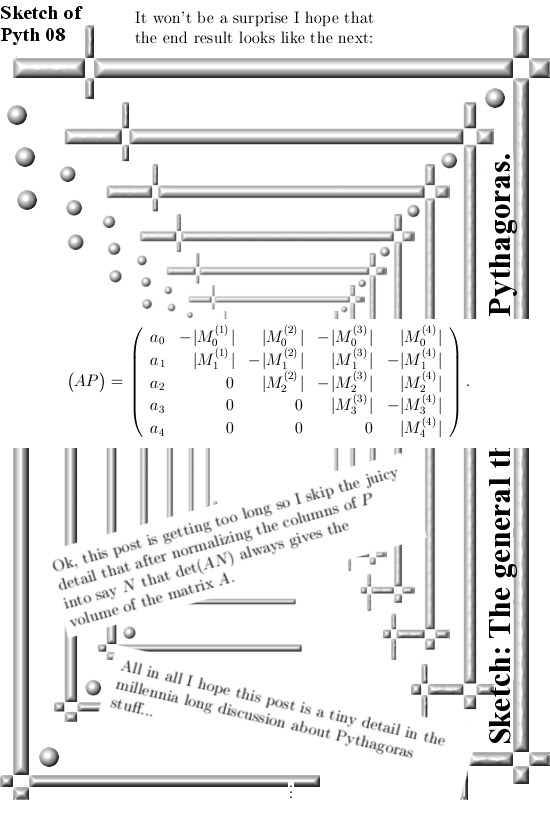
I have this pdf about a year now. Last year when I was doing that matrix form of the theorem of Pythagoras I came across this pdf and I saved it for another day.
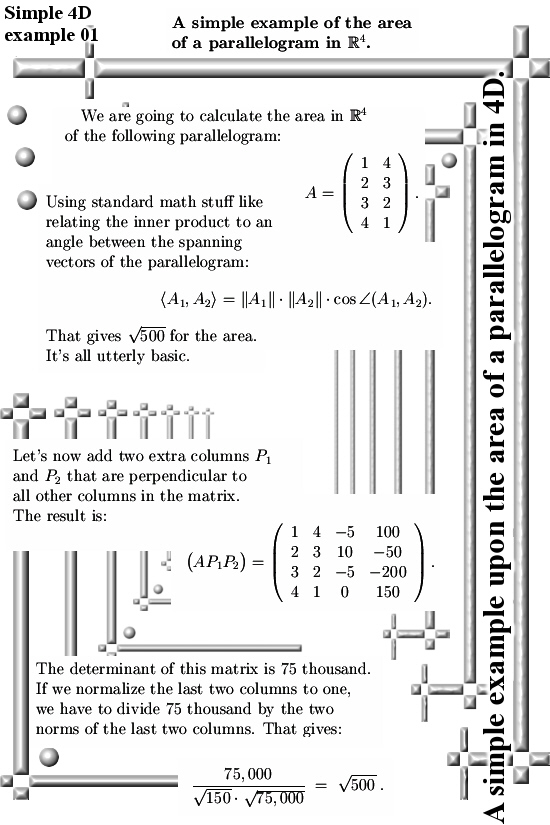
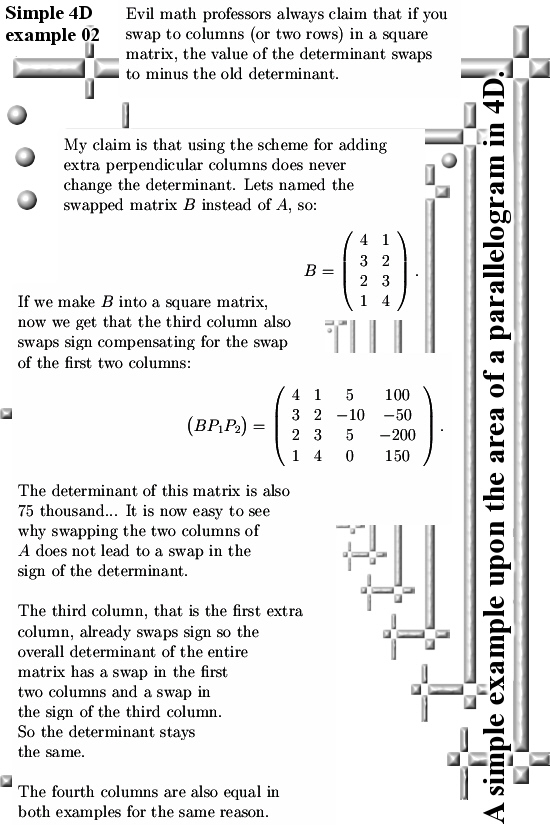
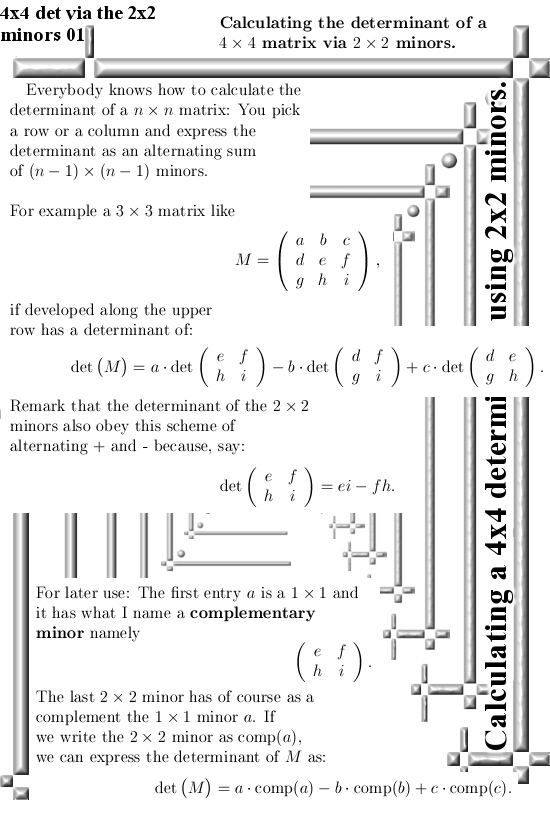
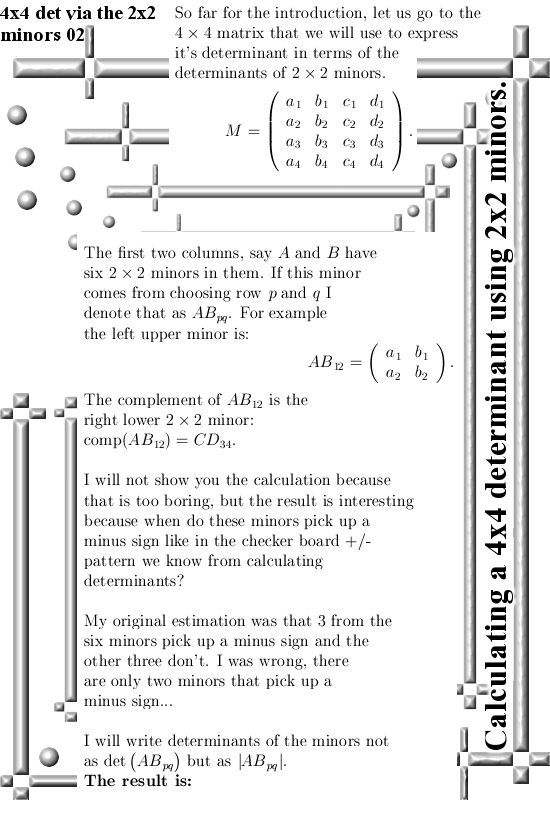
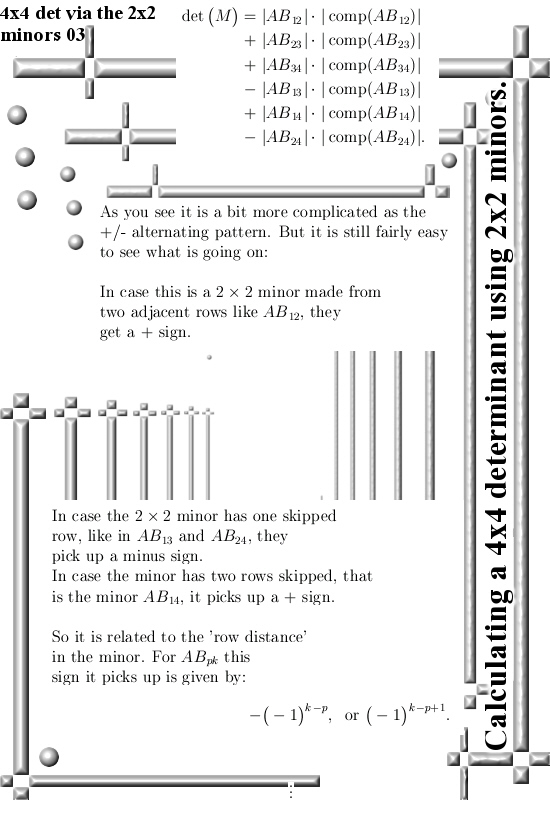
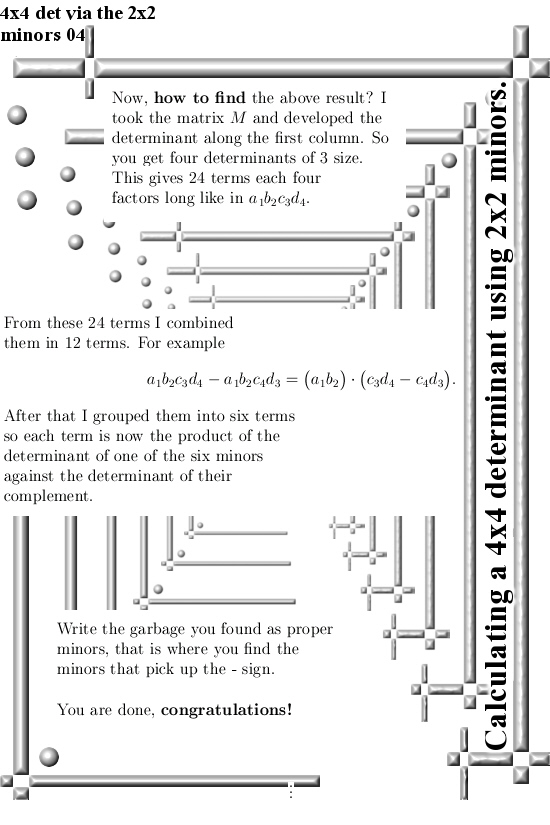
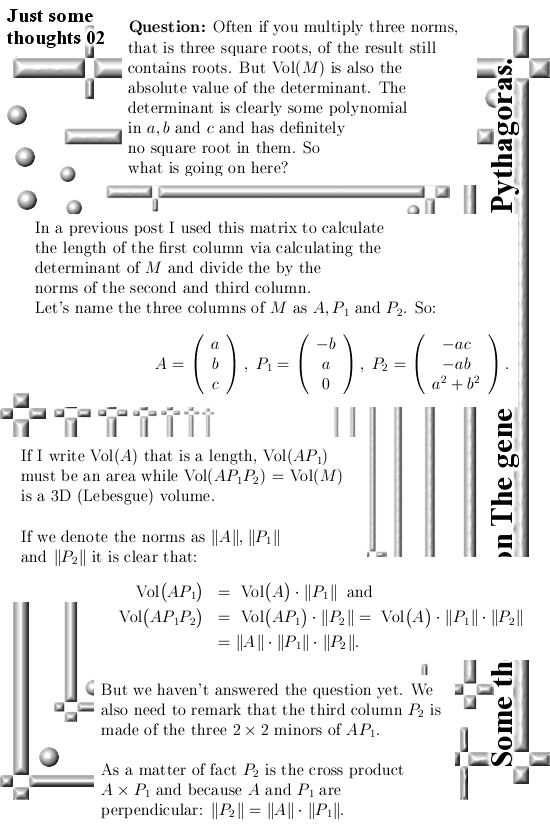
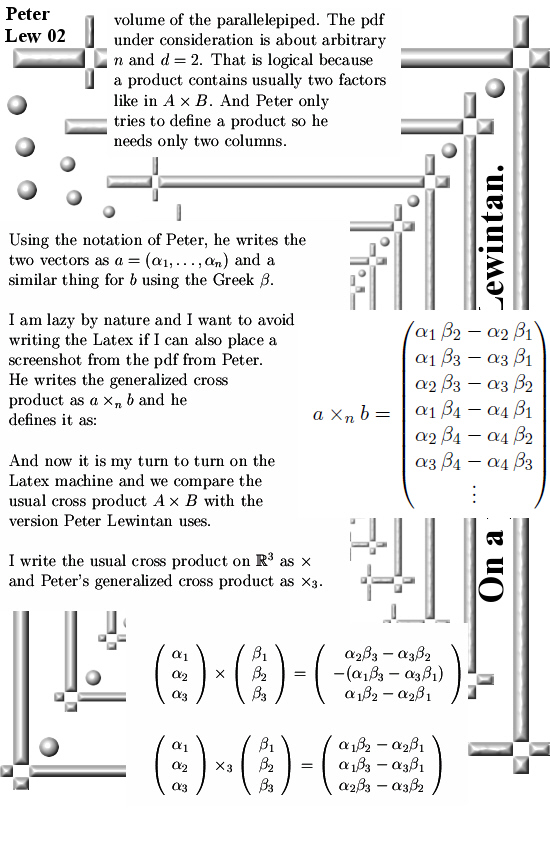
Last year when working on that matrix Pyth stuff you always get a large bunch of those determinants of those minor matrices. And I thought like “Hey you can put them in an array and in that case the length of that array is the volume of that parallelepipid”. Well in this pdf Peter is just doing that: He does not use a nxd matrix but only two columns because the goal is to make a product.
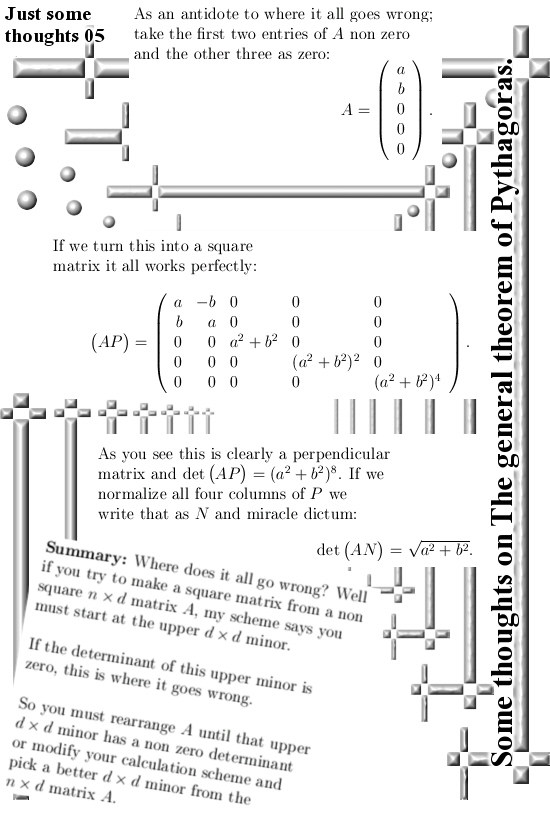
Last year after say an hour of thinking I decided to skip that line of math investigation and instead concentrate more on if it would be possible to make that none square nxd matrix into a square nxn matrix.

Another reson to save this pdf for a later day was the detail it was also about differential operators. Not that I am very deep into that but the curl is a beautiful operator and as you likely know can be expressed with the help of the usual cross product in three dimensions. To be honest I considered this part of the pdf a bit underwhelming. I really tried to make some edible cake from that form of differential operators but I could not give a meaning to it. May be I am wrong so if you want you can try for yourself.

The pdf contains much more as the above, a lot of cute old identies and also some rather technical math that I skipped because sometimes I am good at being lazy…;)

My comments are four pictures long and after that I will try to hand the dpf from Peter into it.

What is it that makes those present day picture generators so bad at things having five fingers? I think those genrative ai machines don’t count on their fingers.

But serious, here is the pdf:

I posted this in the category Pythagoras stuff because it is vaguely related to that matrix version of the Pythagoras theorem.
Ok that was it for the time being. May be the next post is from some nutty professor who claims in a video that 3D complex numbers don’t exist. Or something completely different. Who knows where our emotions bring us?

This is one of the details I should have posted last year. So this post is some mustard after the meal. The content is just two pictures long. In it I show you how to calculate the area of a parallelogram in 4D space. After that we swap the two columns and use the same method again. In both cases the area of the parallelogram equal the square root of 500.
If you read stuff from this website you likely have enjoyed some classes in linear algebra, likely you know that if you swap two columns (or two rows) in a square matrix, the determinant changes sign.
But the way we turn a non-square matrix into a square matrix is done in such a way that it has to return a positive (or better: non-negative) number.
In this example you can see that if you swap the two spanning columns of the parallelogram, the first extra column or the third column in our final matrix also chages sign. So the overall determinant of the 4×4 final matrix ‘observes’ a swap in the first two columns and also a swap in the sign of the third column. Hence the determinant does not change sign…

Originally I only needed a few cute looking formulas for use on the other website. That are the two matrices below. But when finished I added some text and as such we have a brand new post for this website.

In this example I did not normalize the extra columns to one so if you want you can play a bit with it and as such observe how their norms are related to the area of the diverse parallograms in here. For example if you calculate the norm of the fourth column, it is the square root of 75,000 while the determinant of the whole 4×4 matrix is 75,000.

As such constructing square matrices like this always leads to the last column having a norm that is the square root of the determinant.
That is a funny property, or not?

Anyway here are the two pictures, the third picture is an illustration of how it was used on the other website. As usual all pictures have sizes of 550×825.

In the third picture I used an old photo of Brigitte Bardot as a background picture. Now both Brigitte and me we looked a lot more fresh back in the time from before they invented the stone age. Our minds were sharp and our bodies fast while at present day we are just another old sack of skin filled with bones, fat and some muscle. Life is cruel..

Ok, lets end this post now and see you around my dear reader.

Yes I know that two posts back I said that this would be the last time we would do Pythagoras stuff like this. On the other hand I was very unsatisfied with that post (title: That weird root formula). Also I had wanted to post the math below before but I did not have the time.
All in all since I was horribly bad in the post upon that weird root formula about how to make extra columns, may this short post compensates a bit for that.
This post starts with a column of four real numbers, say a, b, c and d. The goal is to keep on adding extra columns such that all columns are perpendicular to each other. Don’t confuse that with an orthogonal matrix, orthogonal matrices also have all their columns perpendicular but the columns are also all of norm one.
For myself I name matrices that have all their columns perpendicular to each other ‘perpendicular matrices’ but this is not a common thing in math communications as far as I know.
I show you two examples here: First I make an extra column based on the a and b entry of our vector. In the second expansion of the same vector I use the middle two entries b and c.
This should serve as examples that make it as transparant as possible how you must use the +/- chessboard pattern that comes with calculations like this.
For understanding this post it comes in very handy if you have done & understand the general way of crafting the inverse of a square matrix. I think most people will see the brilliant +/- chessboard scheme there for the first time in their lives.

I don’t know much about the history of math, but I like it that the +/- chessboard scheme has no human name attached to it like in “Hilbert space”. I guess this chessboard pattern emerged slowly over the cause of a few decades with contributions of many people. So in the end there was nobody to name it too because this big success just had to many fathers.

Another explanation for the lack of a human name to the famous +/- chessboard pattern is that the person who for the first time chrystal clear wrote out the stuff, this person was not an overpaid professional math professors. But say an amateur just like me. Well in those good old times just like now, the overpaid math professors can’t give credit to such an undesireable person of course…
Yet not all is negative when it comes to professional math professors: They are still very good at telling anybody who wants to hear it that: “We tried but we could not find the three dimensional complex numbers”.

After all that human blah blah blah, why not take a look at the three pictures?

That was it for this post.

It took an amazing amount of time to finish this post. When I started it you could still bike in the city with your shorts on. And now it is freezing cold at the start of winter. I posted over 220 posts on this website but I never experienced such a long lasting writers block on my behalf.

I think the start was much to impulsive, mostly I take more time before I pick a subject for the next post. This time I did not do that and soon I ran into writers regret: Why did I start this BS that is far to complicated to explain in a few lines of writing?

Even the beginning is dumb to do: It makes the reader think it is something solely on that space and it’s unit ball. And that dumb deed alone is a misrepresentation of what the weird root formula is about.

Anyway it is what it is and may be it is a good thing to show you that I can be very impulsive to. And in the science of math that is not a good thing.

Since it has been a while I posted the last post on the matrix version of our beloved theorem of Pythagoras, readers who are new must use the search function on the website or just look into the category ‘Pythagoras stuff’. The matrix version of the Pythagoras theorem is not that hard to formulate but hard to prove. It goes like this:

Given some n x d matrix A made up of d columns, if the d columns are linearly independent this defines or represents a d-dimensional parallelapiped. What can be said about the d-dimensional volume, or better the square of this volume?
It seems that the matrix A has lots of d x d minor matrices and if you take the determinant of these minors, square them they will add up to the desired square of the volume of A.

As you see: The result is not that hard to understand while our small human brain has trouble to cough up 20 proofs in 40 minutes.

The key idea of the weird root formula is that you can apply an alternative way of calculating determinants: Multiplying determinants of minors against determinant of their so called complement. So for the matrix A that should give it’s d-dimensional volume.

But if you expand the matrix A with an extra column perpendicular to all columns of A, say you get AP_1 and of course you normalize P_1 to length 1, you can repeat the whole thing on the expanded matrix. This goes on until the matrix A has been made a square matrix that I denote as AP.
In this post I use the notation (AP) for the square matrix so you must never view AP as the product of two matrices or so because that is not what it is…

This post if four pictures long but it has to be remarked I skipped how to find that +/- scheme you need for calculating determinants this way.

So after all this time this Pythagoras stuff is published. All in all it is a cute idea, that weird root formula can be applied not only to that starting matrix A but also on every extension with extra perpendicular columns.

End of this post.

The last week I have been stuck in a writers block. I started writing on another post on the Pythagoras matrix version stuff and I just don’t know how to proceed. On the one hand I want to tell a cute so called ‘weird root formula’ while I want to avoid using that +/- scheme that is difficult to explain and has nothing to do with what I wanted to say.

May be I put the stuff I don’t want to talk about in a separate appendix or so. That sounded like a good idea two weeks ago but I’m still not working on it…

But it is about time for a new post and because my own Pythagoras stuff is glued to my writers block, the mathologer had a new video out about Pythagoras stuff the mathologer’s way. If you have seen vids from the mathologer before, you know he likes visual proofs to back up the math involved. The mathologer works very differently from me, I got hooked up to that matrix version earlier this year while he is doing stuff like trithagoras in a very cute manner.

The video is about half an hour long, just pick what you like or what you need and move on to other things. Digesting all stuff in a video from the mathologer always takes more time as the video is long! So you are not looking at just another insignificant idiot like me…;)

The next video is from Michael Penn. Now Michael has that typical American attitude of putting out one video a day. Often they are not bad if you take into consideration this must be done every 24 hours. But his treatment of (x + y)^n = x^n + y^n is just horrible. If you look like Michael for solutions on the real line it is easy to understand this cannot work.
Yet last year all my counter examples to the last theorem of Pierre de Fermat were always based on this (x + y)^n = x^n + y^n equation.
Take for example the natural numbers modulo 35.
In this simple case we already have a cute counter example to the last theorem of Pierre de Fermate, namely:
12^n = 5^n + 7^n mod 35.

Why did Michael choose this fucking stupid space of real numbers for this equation that is the basis of a lot of counter examples to the last theorem of Pierre de Fermat? May be the speed of new videos is a thing here.

Ok, that was it for this post. See you around…

I remember that in the past a few times I tried to write determinants of say a nxn matrix in determinants of blocks of that matrix. It always failed but now I understand the way the matrix version of the theorem of Pythagoras goes, all of a sudden it is a piece of cake.
In this post I only give an example of a 4×4 matrix. If you take the first two columns of such a matrix, say AB, this is now a 4×2 matrix with six 2×2 minors in it.
If we name the last two columns as CD, for every 2×2 minor in AB there is a corresponding complementary 2×2 minor in CD. For example if we pick the left upper 2×2 minor in our matrix ABCD, it’s complement is the right lower 2×2 minor at the bottom of CD.
If you take the determinants of those minors and multiply them against the determinants of their complements, add it all up with a suitable +/- pattern and voila: that must be the determinant of the whole 4×4 matrix.

This method could more or less easily expanded to larger matrices, but I think it is hard to prove the +/- pattern you need for the minors of larger matrices. Because I am such a dumb person I expected that half of my six 2×2 minors pick up a minus sign and the other half a plus sign. Just like you have when you develop a 4×4 determinant along a row or column of that matix. I was wrong, it is a bit more subtle once more confirming I am a very very dumb person.

I skipped giving you the alternative way of calculating determinants: The determinant is also the sum of so called signed permutations on the indices of their entries. If you have never seen that I advice you to look it up on the internet.

Because I skipped excisting knowledge widely available already, I was able to do the calculation in just four images! So it is a short post. Ok ok I also left out how I did it in detail because writing out a 4×4 determinant already has 24 terms with each four factors. That’s why it is only four pictures long in this post…

If you want you can also use that expression as the determinant as a sum of signed permutations. It is a very cute formula. Wiki title:
Leibniz formula for determinants.
And a four minute video, it starts a bit slow but the guy manages to put in most of the important details in just four minutes:

Ok, that was it for this post. I filed it under the category ‘Pythagoras stuff’ because I tried similar stuff in the past but only with the knowledge into the matrix version of the Pythagoras theorem, it all becomes a bit more easy to do.

Thanks for your attention.

To be honest this post is not carefully thought through. I felt like starting to write and at first I wanted to write it more into the direction of a proof based on the volumes of the parallelepiped and it’s expansion columns. But then I realized that my cute calculating scheme of turning a nxd matrix A into a square nxn matrix AP could go wrong. So I wanted to address that detail too but I hadn’t thought it out enough.

The answer to why it can go wrong is rather beautiful: Take any nxd matrix (of course the number of columns cannot exceed n because that is not a proper d-dimensional parallelepiped) say a 10×3 matrix. The three columns span a parallelepiped in 10-dimensional real space.
The ‘smallest’ parallelepiped that still has a three dimensional volume is one of the many minors possible in the 10×3 matrix. So with ‘smallest’ I mean the parallelepiped that uses the least number of coordinates in our 10-dimensional space.
Now in my calculating scheme, an algorithm if you want, I said you to start at the top of the matrix A and add more and more columns. But if A is made of just one 3×3 minor, say at the bottom of A, it is crystal clear my calculating scheme goes wrong because it now produces only zero columns.

And if that happens, when in the end you take the determinant of the square matix AP you get zero and of course that is wrong. These are exceptional cases, but it has to be addressed.


Of course there is no important reason for the calculation scheme to start at the top of the matrix, just start at the position of the lone 3×3 minor. In general: If you start with a nxd matrix, ensure your first expansion column is not a zero column. After that the next expansions all should go fine.

This post is five pictures long. If you haven’t mastered the calculation scheme of how to turn a non-square matrix into a square matrix you must first look up previous posts until you have a more or less clear mental picture of what is going on with this.

Ok, that was it for this post on the highly beautiful calculation scheme for the volumes of parallelepipeda in higher dimensions.

A long long time ago you likely learned how to calculate the sine in a rectanglular triangle. And that was something like the length of the opposite side devided by the length of the hypotenuse. But now we have those simple expressions for the volume of a non-square matrix, we can craft ‘sine like’ quotients for the minors of a matix against it’s parent matrix.
I took a simple 4×2 matrix so 4 rows and 2 columns, wrote out all six 2×2 minors and defined this sine like quotient for them. As far as I know this is one hundred percent useless knowledge, but it was fun to write anyway.
Likely also a long time ago you learned that if you square the sine and cosine of some angle, these squares add up to one. In this post I formulated it a little bit different because I want to make just one sine like quotient and not six ones that are hard to tell them apart. Anyway, you can view these sine like quotients as the shrinking factor if you project the parent matrix onto such a particular minor. With a projection of course you leave two rows out in you 4×2 parent matrix, or you make these rows zero. It is just what you want.
The parent 4×2 matrix A we use is just a two dimensional parallelogram that hangs in 4D space, so it’s “volume” is just an area. I skipped the fact that this area is the square root of 500. I also skipped calculating the six determinants of the minors, square them and add them up so we must get 500. But if you are new to this kind of matrix version of the good ol theorem of Pythagoras, you definitely must do that in order to gain some insight and a bit of confidence into how it all works and hangs together.

But this post is not about that, it only revolves around making these sine like quotients. And if you have these six quotients, if you square them and add them all up, the result is one.
Just like sin^2 + cos^2 = 1 on the real line.

Please notice that the way I define sine like quotients in this post has nothing to do with taking the sine of a square matrix. That is a very different subject and is not a “high school definition” of the sine quotient.
This post is just three pictures long, here we go:

So after all these years with only a bunch of variables in most matrices I show you, finally a matrix with just integer numbers in it… Now you have a bit of proof I can be as stupid as the average math professor…;)

But serious: The tiny fact all these squares of the six sines add up to one is some kind of idea that is perfectly equivalent to the Pythagoras expression as some sum of squares.
Thanks for your attention.