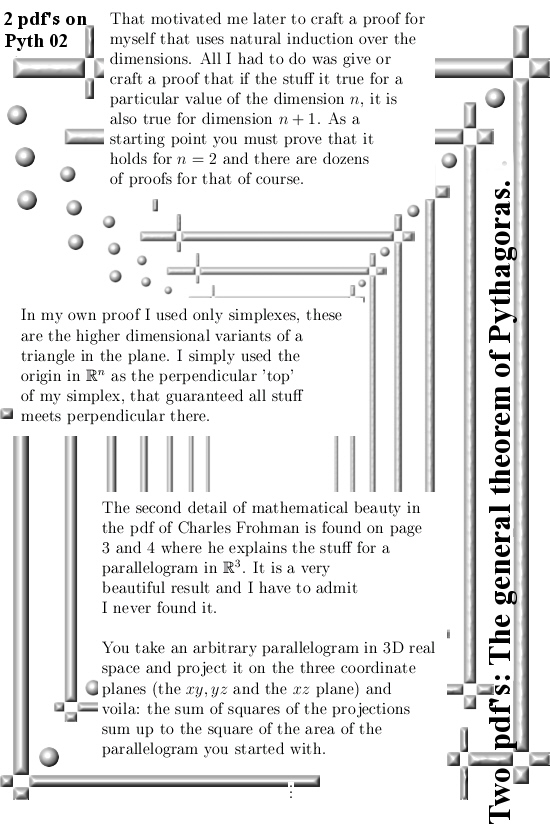
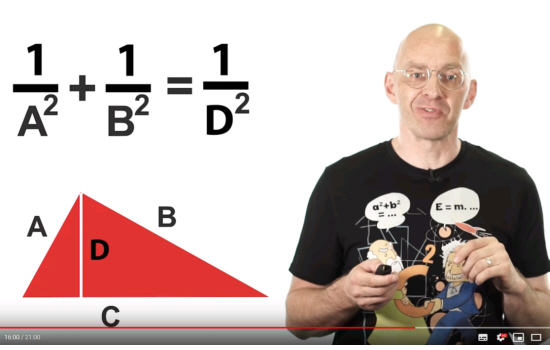
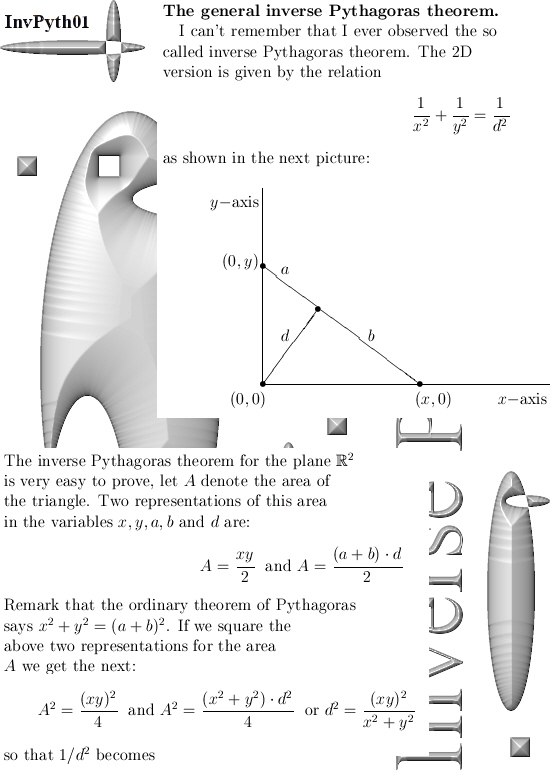
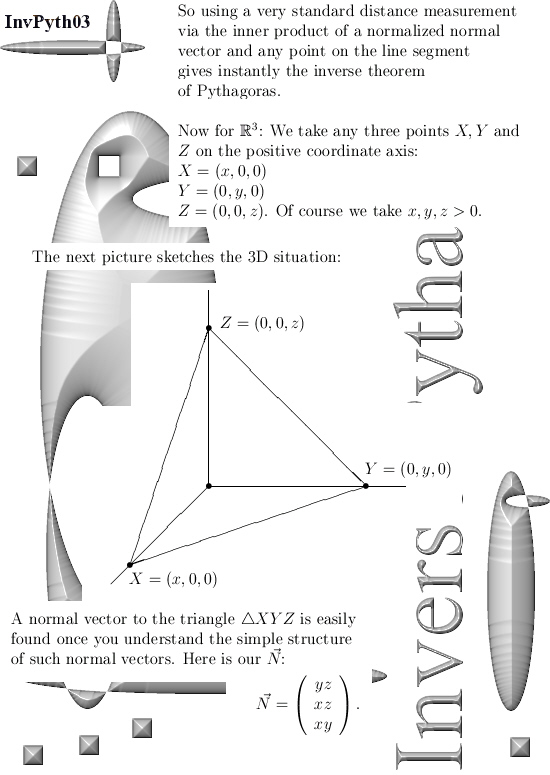
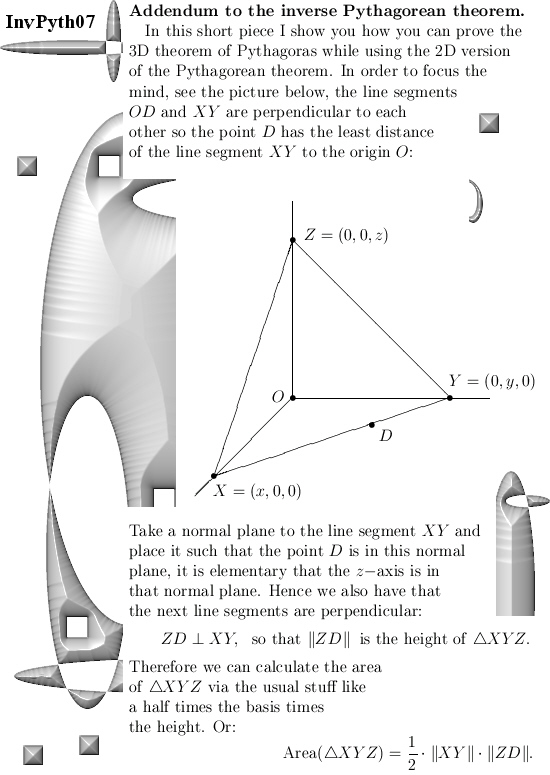
A few posts back I showed you that pdf written by Charles Frohman where he shows a bit of the diverse variants of the more general theorem of Pythagoras there is. At school you mostly learn only about the theorem for a triangle or a line segment and it never goes to anything else. But there is so much more, in the second half of this post I show you three vectors in 4D space that span a parallelepiped that is three dimensional. From the volume of such a thing you can also craft some form of Pythagorean theorem; that paralellepiped can be projected in four different ways and the squares of the four volumes you get equals the square of the original parallelepiped.
I would like to remark I hate that word ‘paralellepiped’, if you like me often work without any spell correction this is always a horrible word…;)

Now my son came just walking by, he reads the title of my post and he remarks: It sounds so negative or sarcastic this ‘full theorem’. And no no no I absolutely do not mean this in any form of negative way. On the contrary I reconmend you should at least download Charles his pdf because after all, it was better compared to what I wrote on the Pythagoras subject about 10 years ago.

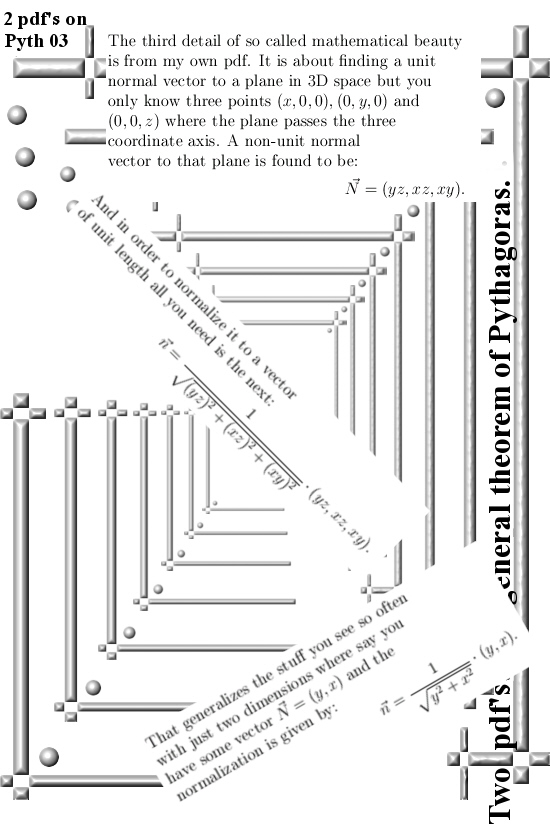
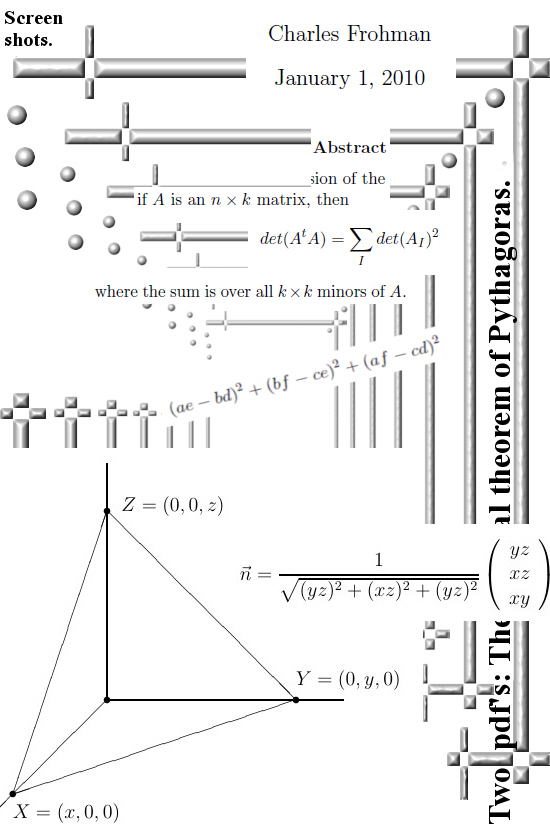
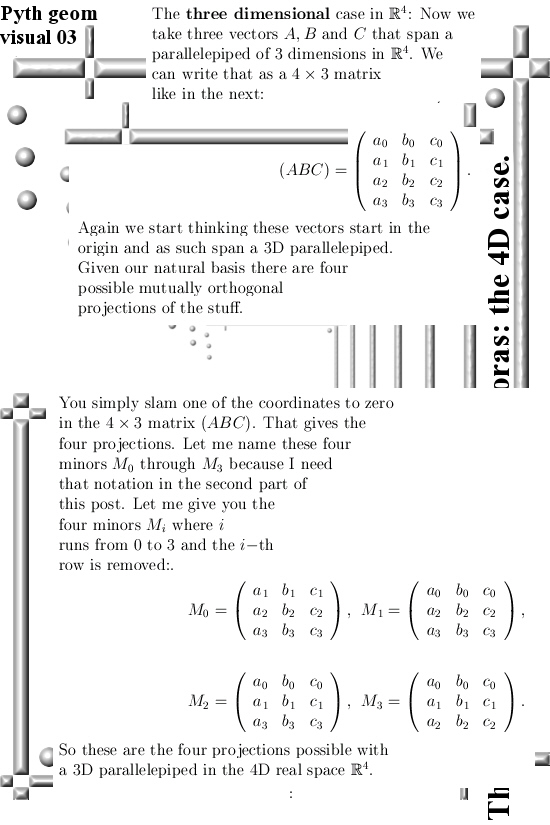
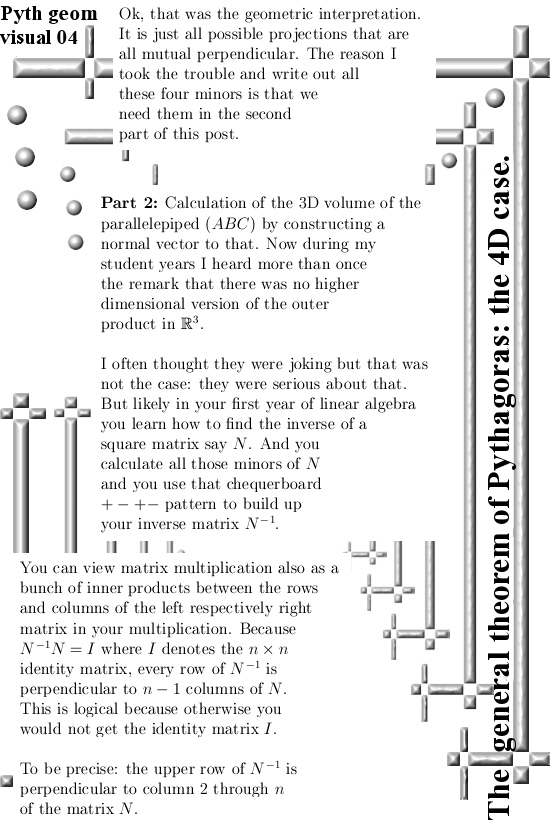
But back to this post: What Charles names the full theorem of Pythagoras is likely that difficult looking matrix expression and from the outside it looks like you are in a complicated space if you want to prove that thing. The key observation is that all those minor matrices are actually projections of that n x k matrix you started with. So that is what the first part of this post is about.

The second part is about a weird thing I have heard more than once during my long lost student years: Outside the outer product of two vectors we have nothing in say 4D space that gives a vector perpendicular to what you started with. I always assumed they were joking because it is rather logical that if you want a unique one-dimensional normal vector in say 4D space, you must have a 3D dimensional thing to start with. That is what we will do in the second part: Given a triple of vectors (ABC) in four dimensional space, we construct a normal vector M to it. With this normal vector, after normalization of course, it gives now a handy way to calculate the volume of any of those paralellepiped things that hang out there.

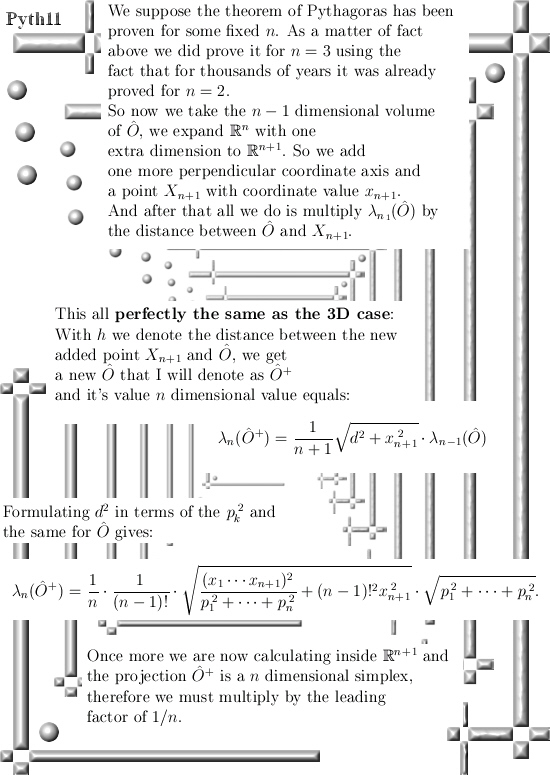
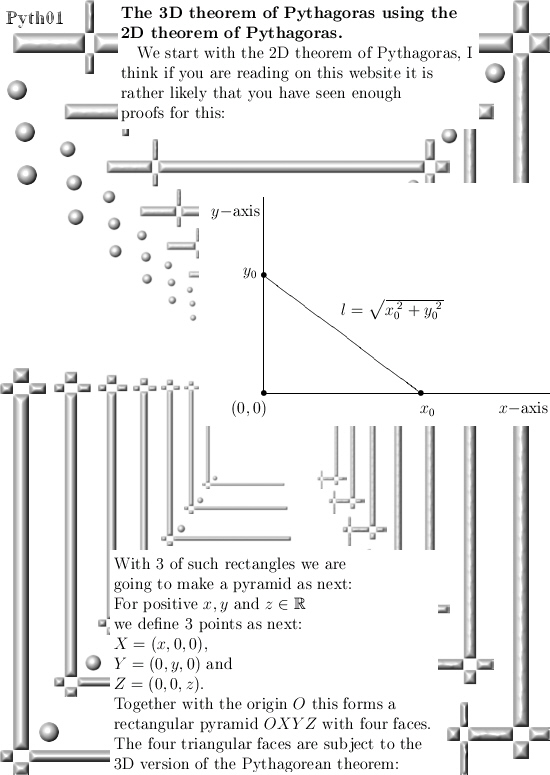
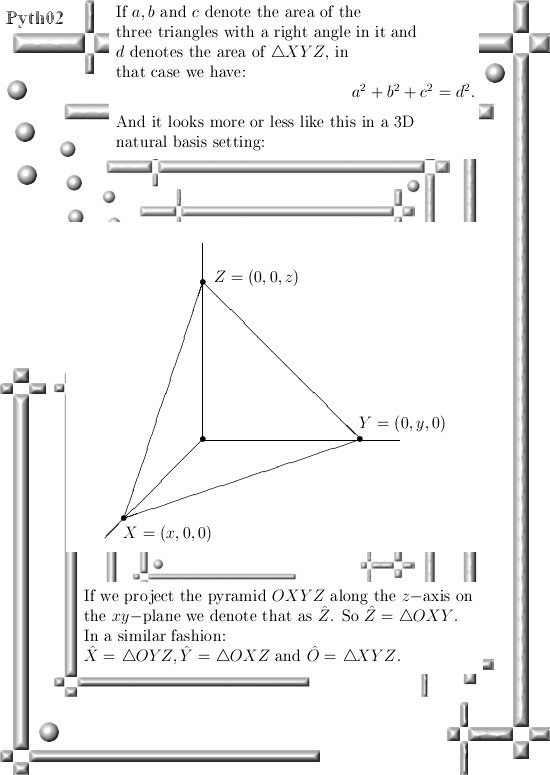
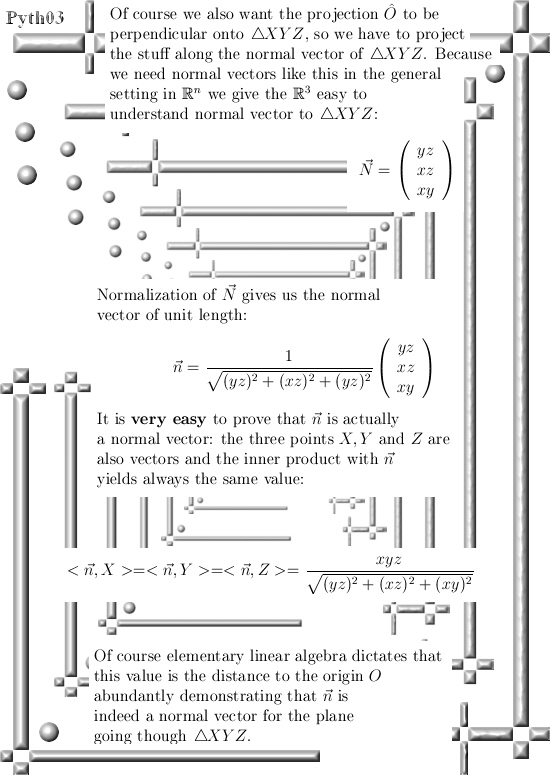
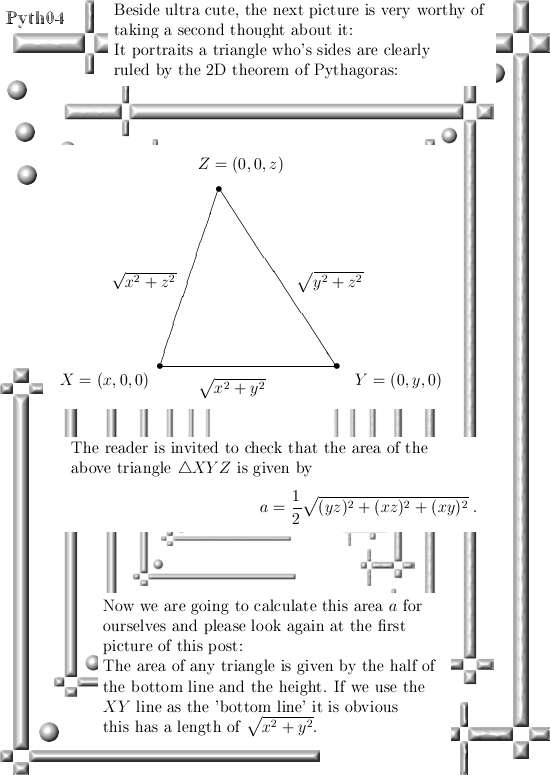
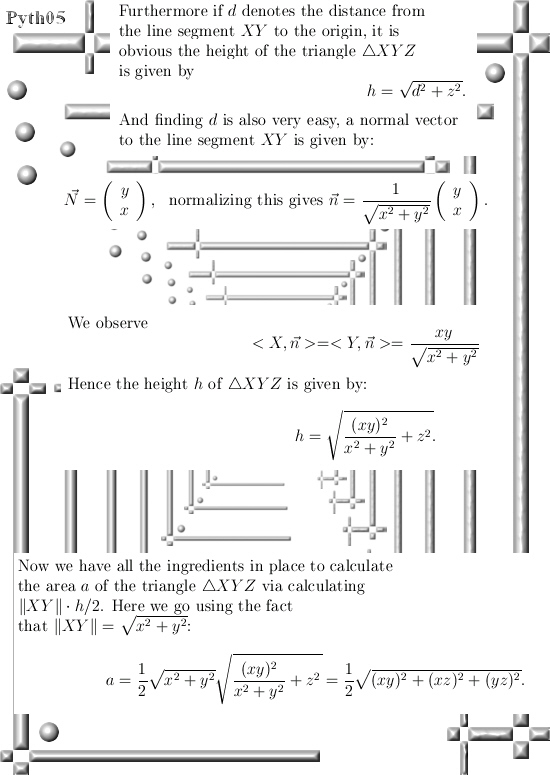
Ok, lets go: Six pictures long but easily readable I hope.

All that is left is trying to find back that link to Charles his pdf.

That was it for this post. I hope you liked it, I surely liked the way you can calculate those paralellapipidedted kind of things. Thx for your attention and see you in the next post.

Last week I started thinking a bit about that second example from the pdf of Charles Frohman; the part where he projected a parallelogram on the three coordinate planes. And he gave a short calculation or proof that the sum of squares of the three projected areas is the square of the area of the original object.

In my own pdf I did a similar calculation in three dimensional space but that was with a pyramid or a simplex if you want. You can view that as three projections too although at the time I just calculated the areas and direved that 3D version of Pythagoras.

Within the hour I had a proof that was so amazingly simple that at first I laid it away to wait for another day or for the box for old paper to be recycled. But later I realized you can do this simple proof in all dimensions so although utterly simple it has absolutely some value.
The biggest disadvantage of proving more general versions of the theorem of Pythagoras and say use things like a simplex is that it soon becomes rather technical. And that makes it hard to read, those math formula’s become long can complex and it becomes harder to write it out in a transparant manner. After all you need the technicalities of your math object (say a simplex or a parallelogram) in order to show something is true for that mathematical object or shape.

The very simple proof just skips that all: It works for all shapes as long as they are flat. So it does not matter if in three dimensional real space you do these projections for a triangle, a square, a circle, a circle with an elleptical hole in it and so on and so on. So to focus the mind you can think of 3D space with some plane in it and on that plane is some kind of shape with a finite two dimensional area. If you project that on the three coordinate planes, that is the xy-plane, the yz and xz-plane, it has that Pythagoras kind of relation between the four areas.

I only wrote down the 3D version but you can do this in all dimensions. The only thing you must take in account is that you make your projections along just one coordinate axis. So in the seven dimensional real space you will have 7 of these projections that each are 6 dimensional…

This post is four pictures long, I did not include a picture explaining what those angles alpha and theta are inside one rectangular triangle. Shame on me for being lazy. Have fun reading it.

So all in all we can conclude the next: You can have any shape with a finite area and as long as it is flat it fits in a plane. And if that plane gets projeted on the three coordinate planes, the projected shapes will always obey the three dimensional theorem of Pythagoras.

Ok, thanks for your attention and although this inner product kind of proof is utterly simple, it still has some cute value to it.

A few months back I found a very good text on more general versions of the good old Pythagorean theorem. Since in the beginning of this text the author Charles Frohman did the same easy to understand calculations as I did a long time ago I more or less trust the entire document. But I did not check the end with those exterior calculations, I don’t know why but I dislike stuff like the wedge product.
The second pdf is from myself, likely I wrote it in 2012 because a proof of a more general version of the theorem of Pythagoras was the first math text I wrote again after many years. After that at the end of 2012 I began my investigations into the three dimensional complex numbers again and as such this website was needed in 2015.

Anyway I selected 3 details from these two pdf’s that I consider beautiful math ideas where of course I skip a definition of what ‘beautiful’ is. After all the property ‘mathematically beautiful’ is not a mathematical object but more a feeling in your brain.

Let me start with four pictures where I look into those 3 selected details, after that I will hang the two pdf texts into this post.

The first pdf is from Charles Frohman. May be you must download it first before you can read it, I should gain more experience with this because the pdf format is such a hyper modern development…;)
The first text is from 2010:

At last my old text from 2012:

(Later I saw there were some old notes at the end of my old pdf, you can neglect that, it has nothing to do with the Pythagoras stuff.)

There is little use in comparing these texts, I only wanted to make a proof that uses natural induction so I could prove the theorem in all dimensions given the fact we have a proof (many proofs infact) for the theorem of Pythagoras with a rectangular triangle. Charles his text is more broader and the main piece is the proof for that determinant version of the theorem of Pythagoras.

At last a remark about the second detail of mathematical beauty: Charles gave the example of a parallellogram where the square of the area equals the sum of squares of the three projections on the three coordinate planes. I think you can take any shape, a square of a circle it does not matter. It only matters it is a flat thing in 3D space. After I found that within the hour I had a proof for the general setting of this problem in higher dimensional real space, may be this is for some future post.

For the time being let us split and go our own ways & thanks for the attention of reading this.

Somewhere last year I just looked some nice video from the Mathologer about the theorem of Pythagoras. And since I myself have found a proof for the general theorem of Pythagoras in higher dimensions, I was puzzled about what the so called ‘inverse theorem of Pythagoras’ actually was.

Could I do that too in my general proof? And the answer was yes, but when I wrote that old proof of the general theorem of Pythagoras it was just a technical blip not worthwhile mentioning because it was a simple consequence of how those normal vectors work.

Anyway to make a long story short, a few days back I likely had nothing better to do and for some reason I did an internet search for ‘the inverse theorem of Pythagoras’. All I wanted to do is read a bit more about that from other people.

To my surprise my own writing popped up as search result number 3, that was weird because I wanted to read stuff written by other people… Here is a screenshot of the answers as given by the Google search machine:

Ok ok, not bad at search result number 3.

Now why bring this up? Well originally I forgot to post to the video that started my thinking in the first place. It is from the Mathologer and here at 16.00 minutes into his video is where my mind started to drift off:

The video from the Mathologer is here (title Visualizing Pythagoras: ultimate proofs and crazy contortions):

It is a very good video, my compliments.

After so much advertisements for the Mathologer, just a tiny advertisement for what I wrote on the subject of the inverse theorem of Pythagoras on March 20 in the year 2018:

What is the inverse Pythagoras theorem?

Ok, that was it. Till updates.

It is already late in the evening, actually it is past midnight so I will keep the text of this post short. It was a nice day today and this evening I brewed the 23-th batch of a beer known as ‘Spin half beer’. (I name it that way because it contains only half of the dark malts I use in the beer known as dark matter…;) so it has nothing to do with electrons).

This is a very basic post about some ‘inverse Pythagoras theorem’ as came flying by in some math video. I was rather surprised that I have not seen it before but there are so many theorems out there using that old fashioned Euclidian geometry that I might have forgetten all about it.

Within 10 minutes I had a good proof for the 2D version of this ‘inverse Pythagoras theorem’. You can find it in the first picture below.

One day later when I was riding a bit around I tried to find the higher dimensional analog of that easy to understand 2D statement or theorem. And as such it crossed my mind the important role a distance number d played in my proof for the general theorem of Pythagoras that acts on simplexes that are the higer dimensional analog of 2D triangles.

Coming home it was easy to write out the details, but for me it was all so simple that does this stuff deserve the title ‘theorem’? Well make up your own mind about that, but if it is not a real complicated theorem it is still a nice and cute result…

This post is six pictures long (all 550×775 pixels beside the last one that needed a bit expansion because the math did not fit properly so that one is 600×775 pixels).

At times it might look difficult but this is only because it is in a general setting when it comes to the number of dimensions, the basic idea’s are all simple things like taking an inner product with a normalized normal vector.

Here are the six pictures:

That is a cute result but for me the normal vector is just as cute but only a bit harder to write out because that part deals with general setting where the dimension n is not fixed.

For the time being is this the end of this post. See you around my dear reader.

__________

Addendum added on 30 March 2018: In the previous post I forgot to place a link to the proof of the general theorem of Pythagoras as I crafted it once a long time ago.

Before this link I would like to show you once more how to prove the general theorem of Pythagoras for the 3D case using only the 2D theorem.

After all, that is the first basic step in my proof for the general theorem of Pythagoras…

Here are the two addendum pictures outlining how this basic step from the two dimensional plane to the 3D space goes:

Here is the link to the proof of the general theorem of Pythagoras:

The general theorem of Pythagoras (second and final post).

The general theorem of Pythagoras (second and final post).

Ok that was it, till updates.

This week I finally did put in the last details of the proof for the general theorem of Pythagoras. Now a long long time ago somewhere like in 1993 or1994 when I found this proof I could only find a very different proof in the official literature.
That proof worked with a matrix, I do not remember how it worked but the important feature is that this proof that used a matrix did not need a special coordinate system.

In the proof that I found I need the origin in the place where all lines, planes, hyper planes etc meet perpendicular so it is pretty natural to use the natural basis in n-dimensional real vector space.
The simplicity of this proof hangs on the construction of a normal vector to a hyper-plane and although I know this result for over two decades once more I was stunned about how easy this normal vector is to find and how easy it is to use the properties of this normal vector in proving the general theorem of Pythagoras.

Because after all; if you are given n + 1 points in n-dimensional space and you must prove something about the convex span of those n + 1 points, most of the time you just scratch your chin a bit, think a bit about it & never make any progress at all…
But using this easy to construct normal vector, instead of a difficult fog you have crystal clear skies over math paradise, what more should a reasonable person want???

In the year 2017 we have a much much better developed internet compared to the times when I originally did find my own version of a proof, but I did not research any of the outlets we have today like, for example, Google books.
If I can find a few good links I will update this post later.

This post is an additional 7 pictures to the previous post, each picture is as usual 550 x 775 pixels.
If you haven’t read the first post containing the first five pictures, please go here.

Once more: The surprising result is how easy to construct this normal vector is…

For myself speaking I am a little bit dissatisfied by notations like O with a hat and a + in the exponent, but I could not find a more easy notation so you simply must swallow that:

O hat lives in n-dimensional space while
O hat with the plus in the exponent lives in (n + 1)-dimensional space…

Ok, this is what I had more or less to say. If I can find a few good links I will post these later and if not see you around & try to get a nice life in case you don’t already have such a kind of life.

A long time ago I found a very simple proof for the general theorem Pythagoras. At the time the general public had almost zero access to internet resources and in those long lost years I could not find out if my proof was found yes or no.

As memory serves, Descartes was the one that gave a proof for the 3D version of the Pythagorean theorem… (But I never did read the proof of Descartes.)

Two weeks back I was cleaning out my book closet so I could store more bottles of beer for the ripening process and I came across that old but never perfectly finished proof.

And it entered my mind again because it is fascinating that just by constructing that perfect normal vector, you make it of unit length, calculate a few higher dimensional volumes and voila:
There is you proof of the general theorem of Pythagoras.

In this post we only look at the 3D example for the theorem of Pythagoras. But already here we use a normal vector together with the 2D theorem of Pythagoras in order to prove the result for 3D space.
Basically this is also precisely the way the proof works in all higher dimensions, ok ok the notations and ways of writing the stuff down is a bit more technical but if you understand the proof in this post you will immediately understand how the general proof works.

The general proof is based on the principle of natural induction, likely the reader is familiar with natural or mathematical induction because beside it’s elegance it is also easy to explain to first year students in exact sciences. Basically you prove some stuff for low values of n, say n = 2 or 3 for 2D and 3D space and after that you do the so called ‘induction step’ where you must show that if it holds for a particular value of n, the stuff you want to prove is also true for n + 1.

Here is a wiki on the subject: Mathematical induction
https://en.wikipedia.org/wiki/Mathematical_induction

__________

This post is five pictures long (size 550 x 775 as usual) so have fun reading it:

In the last line of the proof it is important to remark that both the length of XY is done with the 2D version of Pythagoras, but the height h of triangle XYZ is also done with the 2D version of Pythagoras. And so you get the 3D version of the famous Pythagoras theorem.

See you in the next post where it is all a bit more abstract and not slammed down to just two or three dimensions. Have a nice life or try to get one.