The official version aka the standard model of particle physics says there is only one kind of electron, all electrons are the same, and their magnetic properties like spin are only a matter of alignment cq anti-alignment with the magnetic field. The standar model treats electrons as tiny magnets.
I think that electrons are magnetic monopoles and as such there are two kinds; a north pole and a south pole kind. But can electrons flip their spin? After all a lot of quantum computing is based on the idea that indeed electrons can flip their spin even stronger: the electron can be in a super position of spin un and down.
Over the years I slowly evolved to the position that the magnetic charge of electrons is permanent. And if the magnetic charge is permanent in that case in the electron cloud of an atom or a molecule, al lot of transitions cannot be done. During those transitions the spin of an electron cannot flip simply because it’s charge is just like the electric charge: permanent.

Now I did not know it but inside a lot of chemistry files you can find a thing known as ‘Spin selection rules’ that give a good description of how an electron can jump up and down the diverse orbitals when it comes to it’s spin. You can also find it under ‘Forbidden transitions’ but also stuff like radioactive decay has forbidden transitions.

An important feature of a forbidden jump in electron transitions is that ther assiciated energy can be observed but that is always on a longer timescale. My impression is that the chemical people don’t understand very good as why this is: Well an electron in some atom or molecule can only ‘flip’ it’s spin as it gets replaced by another electron.

Example: The 21 cm radio frequency in radio astronomy. Photons with a wavelength of 21 cm come from atomic hydrogen that undergoes a spin flip to it’s lowest potential energy configuration when it comes to magentism.
But if that can only be done by other electrons bumping into that hydrogen atom, that says something about the electron streams in vacuum from where the 21 cm radiation is coming.

Here a simple picture of what is allowed and what not:

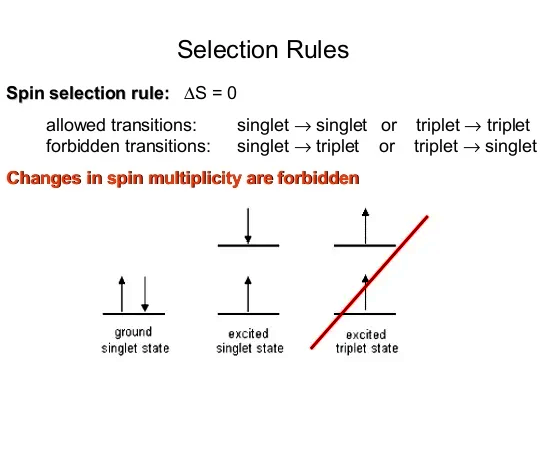
It is very well known inside the science of chemistry that energy states like those singlet and triplet stuff above are very close to each other. So how it is possible that just some thermal shaking or good old molecular vibrations do never flip the spin of an electron?

If all that mumbo jumbo about electrons was true, why can’t some heat or some vibrations make that sole electron flip it’s spin? Do we get that nonsense like “If you think you understand quantum mechancis, in that case you don’t understand quantum mechanics” one more time?

And I admit that too: If you are that stupid to view the electron as a tiny magnet, yes indeed the science of particle physics but also chemistry becomes very hard to understand. It’s loaded with weird stuff all over the place. In chemical bonding the electrons in a pair must always have opposite spins but in permanent magnets the spins must always be aligned.

May be it is time to split my dear reader. See you in the next post.