This update is 10 pictures long, the pictures are sized 550 by 775 pixels.
This update covers more or less everything, but I still have to explain how you find the six coordinate functions the poeple will need in order to see if these kind of complex numbers give the same result as ordinary complex numbers from the complex plane.

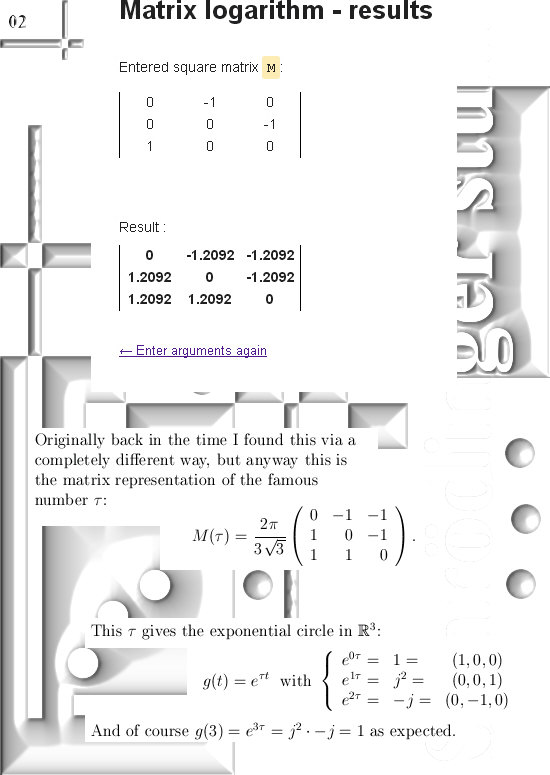
For those that cannot wait: In the post from 03 April I posted a teaser picture with the coordinate functions in 3D, if you multiply this against the e to the power i pi alpha thing in this update you have the six coordinate functions…

Ok ok you neatly have to write them out, but basically it is all there.

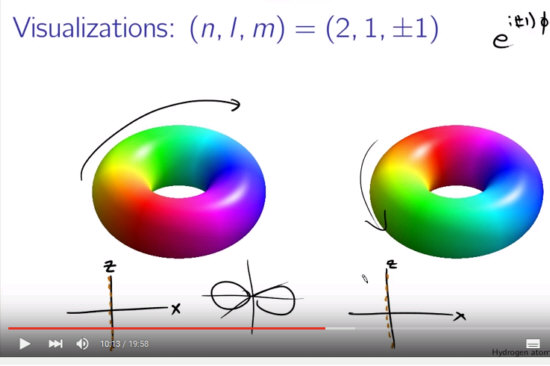
At first I was thinking it would be hard to get different results using these higher dimensional complex numbers, but when talking about atomic and molecular orbitals it might be more subtle than it looks. At the end I will post a video where some physics guy shows all kinds of orbitals related to hydrogen but his stuff is different from the pictures we observe in chemistry.
He explains this by saying that the people from chemistry always take a super-position of two wave-blobs and as such it gets oriented along the y-axis say.
If you would take super-positions of my 3D complex numbers you will get very similar results. look at the drawing in the one before last picture:
Take a super-position of an exponential circle and it’s conjugate and observe it must have the same behavior as 2D numbers from the complex plane.

(In that drawing your eys is supposed to be along the line through zero and alpha, so zero is right behind the center of the shown circle…)

Enough of the bla bla bla, here are the 10 pictures:

Click on the picture to get a larger version of the drawing:

Now finding these atomic & molecular orbitals is very hard, for simple atoms like hydrogen it is doable but what about uranium or some nice protein with only 3693 atoms in it?

All that kind of stuff falls under what we name n-body problems and for n above 3 it seems impossible to find exact analytical solutions.

There is a nice video out there explaining a bit more on the topic of finding the shapes of atomic & molecular orbitals. It is from Brant Carlson and has the title Hydrogen atom wavefunctions:

Ok, that was it for today. Till updates.