Monthly Archives: November 2023

2D elliptical and hyperbolic multiplications.

2D multiplications, Matrix representation

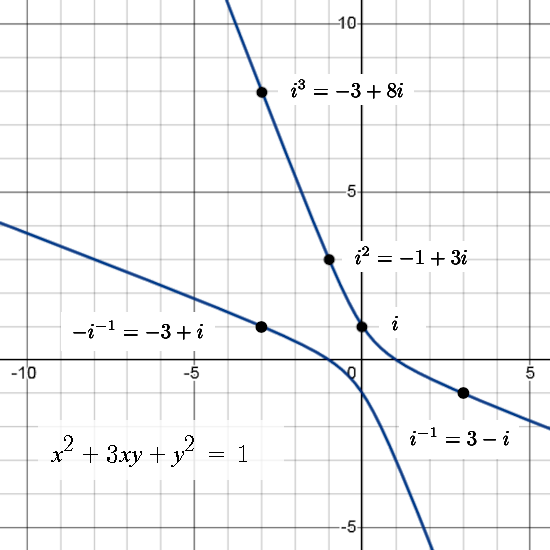
If you change the way the multiplication in the complex plane works, instead of a unit circle as the complex exponential you get ellipses and hyperbola. In this post I give a few examples, where usually the complex plane is ruled by i^2 = -1 we replace that by i^2 = -1 + i and i^2 = -1 + 3i.
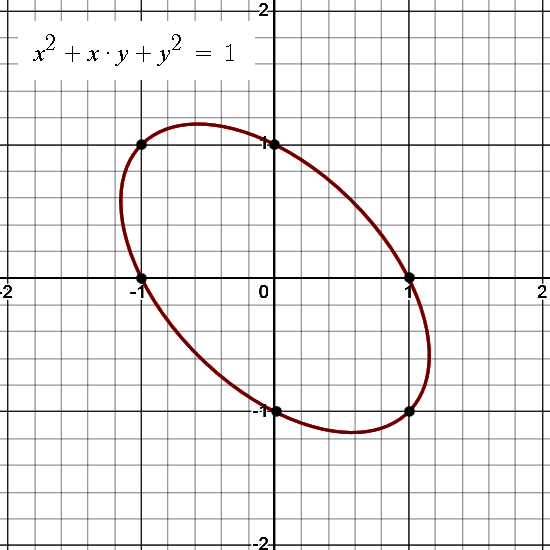
In the complex plane the unit circle is often defined as the solution to the complex variable z multiplied against it’s conjugate and then solve where this product is one.
There is nothing wrong with that, only it leads to what is often told in class or college and that is: The norm of a product of two complex numbers is the product of the norms. And ok ok, on the complex plane this is true but in all other spaces the I equipped with a multiplication it was never true. It is the determinant that does all the work because after all on the complex plane the determinant of a matrix representation of the complex variable z is
x^2 + y^2. (Here as usual z = x + iy for real valued variables x and y.)

Therefore in this post we will solve for det(z) = 1 for the two modified multiplications we will look at. I did choose the two multiplications so that in both cases det(i) = 1. That has the property that if we multiply and z against i, the determinant stays the same; det(iz) = det(z).

I simply name complex z with integer x and y also integers, a more precise name would be Gaussian integers to distinguish them from the integers we use on the real line. Anyway I do not think it is confusing, it is rather logical to expect a point in the plane with integers coordinates to be an integer point or an integer 2D complex number z.

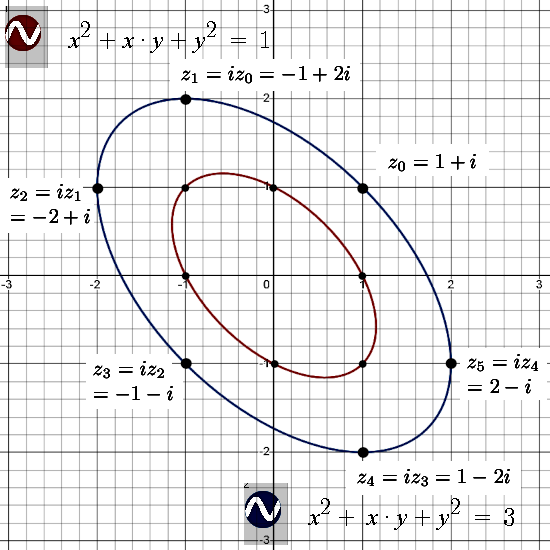
Beside the ellipses and hyperbola defined by det(z) = 1, or course there are many more as for example defined by det(z) = 3. Suppose we have some integer point or z on say det(z) = 3, if we multiply that z by i you stay on that curve. Furthermore such a point iz will always be an integer point to because after all the multiplication of integers is always an integer itself.
That is more or less the main result of this post; by multiplication with the modified imaginary unit i you hop through all other integer points of such an ellipse or hyperbole.
(By the way I use the word hyperbola to be the plural of hyperbole but I do not know if that is the ‘official’ plural for a hyperbole.)

What I found curious at first is the fact that expressions like z = -3 + 8i can have an integer inverse. But it has it’s own unavoidable logic: The 2×2 matrix representation contains only (real) integers and if the determinant is one, the inverse matrix will have no fractions whatsoever. The same goes for any square matrix with integer entries, if the determinant is one the inverse will also be a matrix with only integer entries.

This post is six pictures long, each size 550×1100 and three additional screen shots where I used the desmos graphics package for drawing ellipses and a hyperbole. At last I want to remark that I estimate these results as shown here are not new, the math community is investigating so called Diophantine equations (those are equations where you look for integer solutions) and as such a lot of people have likely found that there are simple linear relations between those integer solutions. Likely the only thing new here is that I modify the way the complex number i behaves as a square, as far as I know math folks never do that.
So let me try to upload the pictures and I hope you have fun reading it.

Funny detail: i^3 = -1.

Ok, that was it for this post. I hope you liked it and learned a bit of math from it. I do not have a good category for 2D numbers so I only file this under ‘matrix representations’ because those determinants do not fall from the sky. And file it under ‘uncategorized’.
Thanks for your attention and see you in a new post.

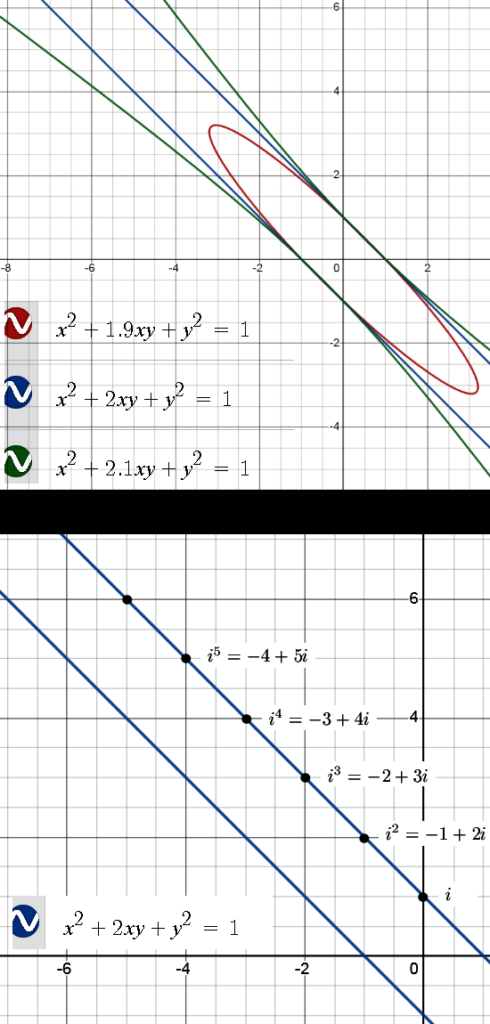
Addendum added 09 Dec 2023: I made a picture for the other website but since I made it already why not hang it in here too? See picture 05 above where we looked at when you get an elliptical multiplication and when the hyperbole version. In the picture below you see a rather weird complex exponential: a straight line. And the powers of i just hop over all those integer values on that line. The multiplication here is defined by i^2 = -1 + 2i. All positive powers hop to the left and upwards, the inverses go the other way. For example the inverse of i equals 2 – i.

Who would have thought that a complex exponential can be a line?

Ok, that was it for this post. Thanks for your attention.

Cauchy-Riemann equations for a ‘golden ratio’ 2D multiplication.

2D multiplications, CR equations

Even if you change the multiplication in the plane away from the complex or split complex multiplication it is always easy to find the famous CR-equations. And if you have those in the pocket you can differentiate functions defined on the space you made ‘just like’ on the real line.

After all the CR-equations only need that the numbers commute, you also need to make sure that all basis vectors have an inverse but that are the only restrictions. As far as I know in the math world of the universities the CR-equations are only used in the complex plane, may be some stuff with multiple complex variables and that’s all there is in that part of the math universe.

Originally I wrote the post in just one go and one day later when I read it I was rewarded with a lot of stupid typo’s. Stuff like mindlessly typing x and y where it should have been a and b, also I added the inverse of the imaginary unit because after all I said it was important in the previous post where we looked at CR-equations in the case of a more general n-dimensional space.

An interesting feature of the two dimensional plane is that the two basis vectors 1 and i always commute no matter what you come up with for i^2.
I hope the reader is familiar with the fact that on the complex numbers you have the square of i being minus one and plus one for the split complex numbers. In this post we will look at a 2D multiplication that is ruled by i^2 = 1 + i, so you can view this as a minor modification of the split complex numbers.

At first I named the multiplication a ‘strange multiplication’ but one day later I realized that the age old golden ratio has the same property as my imaginary unit i. If you square the golden ratio, that is also the same as the golden ratio plus one. So I renamed it to the golden ratio multiplication. I know it is a little click baity because the golden ratio itself is not used but only the polynomial equation you need to calculate the golden ratio. Universities have their multi-million marketing budgets, still can’t find 3D complex numbers by the way and I have my free tiny click baity golden ratio multiplication. I think it is an allowed sin.

Did you know that if there is something wrong with a product, it always needs massive marketing budgets. Just look at Coca Cola, without the advertisements the stuff should gradually sell less and less because it is not a healthy product. You can say it is an unhealthy product so there is something wrong with it and as such it needs all that marketing stuff in order to survive.

This post is only four pictures long, I hope it is a bit more easy to digest because it is only two dimensions. So lets go to the math in the four pictures:

Ok, that was it for this post. Thanks for your attention.