Monthly Archives: September 2021

What happens to a Frey elliptic curve if we take it modulo 35?

Last Fermat theorem

Of course we have to take a Frey elliptic curve based on one of the counter examples to the last theorem of Pierre de Fermat for this ‘take it mod 35’ to be meaningful.
Welcome by the way!

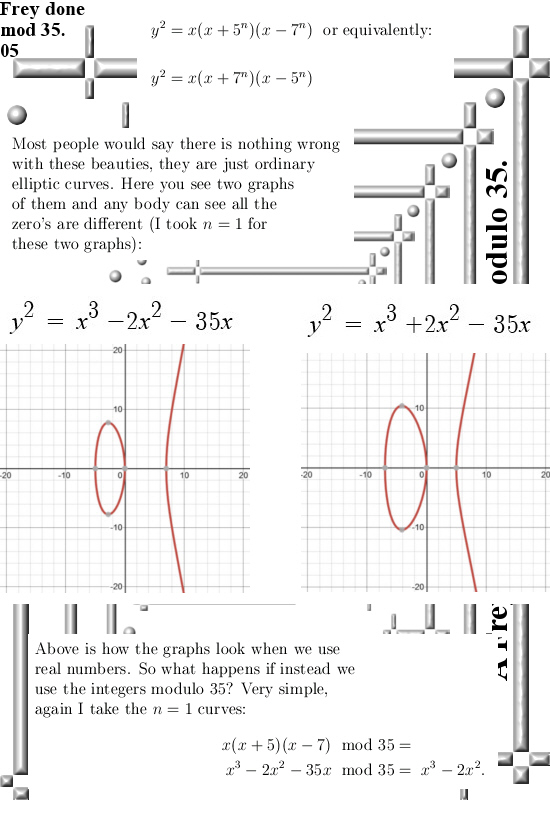
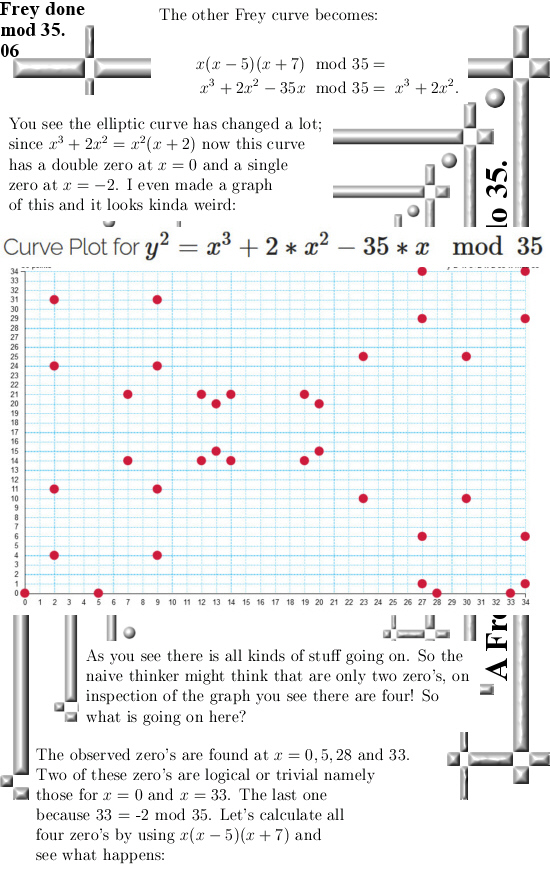
A few months back I encountered this problem for the first time and the determinant of all of those Frey elliptic curves is always zero because it contains the factors that ensure it is a counter example to the last Fermat theorem. As such these two factors are always a pair of divisors of zero and as such if you multiply them you get zero. I did not give it a second thought, only remarked the determinant is zero and as such this likely spells some trouble for such a Frey elliptic curve. Recall that if the determinant is zero, there is at least one double zero to be found in your equation. Two weeks back I looked at it with a bit more detail and the result was rather surprising: The cubic part of such a Frey curve indeed gets some double zero, but all in all in the space of integers modulo 35 the thing has four zero’s! But all these Frey curves go like
y^2 = x(x + A)(x – B) so the ‘x-part’ is a degree 3 polynomial. And a 3 degree polynomial has at most 3 zero’s, or not?

Wrong! A 3 degree polynomial has at most 3 zero’s (or precisely 3 zero’s if you count with multiplicity) but in spaces with divisors of zero it is possible to get extra zero’s. On the spaces of 3D complex and circular numbers it is easy to find a parabola with 3 zero’s. Take p(x) = x^2 – x. If you solve for p(x) = 0 you basically try to find numbers that are their own square. After all if a number is it’s own square, there is no denying that
x^2 – x = 0. Of course x = 0 and x = 1 are their own square, but on the three dimensional complex and circular numbers the center of the exponential circle has also that impotant propery. The center is usually denoted as the number alpha and yes that is a zero too. Yet you cannot use such an extra zero in a factorization of such a parabola. The factorization is and stays
x(x – 1) and if we substitute alpha in we get alpha(alpha – 1). But ha ha ha these last two factors are a pair of divisors of zero and that is why it’s zero…

I also found a cute applet that you can use for making graphs of elliptic curves modulo a single prime number. Most of the time I needed modulo 35 or anything with two prime numbers in it and the applet tries to warn me every time when I do that. I also made a few graphs from counter examples to the last theorem of Pierre de Fermat with it. That was relatively funny and made me decide to write this post. Of course we do not need some applet to validate my counter examples to the last theorem because there is plenty of proof. But it was funny anyway.

Links to the two relevant applets:
Elliptic curves over finite fields, and
Curves over finite fields. With the last applet you can make those counter examples to the last theorem of Pierre de Fermat because it allows you to use exponential expressions. It has to be remarked that the applet is not so good at exponential series so already at the stuff modulo 35 it runs awry and returns gibberish instead of a nice flat zero.

This post grew longer as planned before hand, but that is with most posts I write. You always think ‘ah that is simple to explain in just a few words’ but if you try that and also estimate the math content of the average math loving person, I always need more and more words to explain the stuff involved… Well so be it.

This post is 9 pictures long in the format or size I use lately: 550×825 pixels.

From modulo 35 and higher the applet starts disfunctioning.

Ok, let’s hope there are no unseen typo’s in the above. I always hate when later I read stuff already published to the internet and find out there are typo’s in it…
The next post is likely an infinite list of counter examples to the last theorem of Pierre de Fermat or it will be about a cute antenna design based on the 3D exponential circles. This cute antenna should produce circular radiation and as far as I know this design is not used anywhere. (I do not know if it is better compared to what we have at present date, after all antenna design is a well developed technical field.)

Ok, that was it for this post.

Three video’s to kill the time in case you are bored to the bone…

3D complex numbers, Last Fermat theorem, Magnetism

A couple of days ago I started on a new post, it is mostly about elliptic curves and we will go and see what exactly happens if you plug in one of those counter examples to the last theorem of Pierre de Fermat. There is all kinds of weird stuff going on if you plug such counter example in such a ‘Frey elliptic curve’. I hope next week it will be finished.

In this post I would like to show you three video’s so let’s start that: In the first video a relatively good introduction to the last theorem of Fermat is given. One of the important details of that long proof is the relation between elliptic curves and so called modular forms. And now I understand a bit better as why math professors go bezerk on taking such an elliptic curve modulo a prime number; the number of solutions is related to a coefficient of such an associated modular form. It boggles the mind because what do those other coefficients mean? As always just around the corner is a new ocean of math waiting to get explored.

Anyway, I think that I can define such modular forms on the 3D complex and circular numbers too so may be that is stuff for a bunch of future posts. On the other hand the academic community is never ever interested in my work whatsoever so may be I will skip that whole thing too. As always it is better to do what you want and not what you think other people would like to see. The more or less crazy result is shown in the picture below and after that you can see the first video.

Yet it might be this does not work on the 3D complex numbers…

Next video: At MIT they love to make a fundamental fool of themselves by claiming that their version of a nuclear fusion reactor will be the first that puts power on the electricity grid… Ok ok, after five or six years I have terminated the magnetic pages on the other website because it dawned on me that the university people just don’t want to read my work. I have explained many many times that it is just impossible that electrons are magnetic dipoles but as usual nothing happens.
Oops, wasn’t it some years ago that Lockheed Martin came bragging out they would make mobile nuclear fusion reactors and by now (the year 2021) there would be many made already? Of course I would never work properly because at Lockheed Martin they to refuse to check if the idea’s of electron spin are actually correct. If electrons are magnetic monopoles all fusion reactors based on magnetic confinement will never work. Just look at Lockheed Martin: So much bragging but after all those years just nothing to show. Empty headed arrogant idiots is whart they are.

And now MIT thinks it is their time to brag because they have mastered much stronger magnetic fields with their new high temperature superconducting magnets. Yes well you can be smart on details like super conducting magnets but if you year in year out refuse to take a look at electron spin and is that Pauli matrix nonsense really true in experiments? If you refuse that year in year out, you are nothing but a full blown arrogant overpaid idiot. And you truly deserve the future failure that will be there: A stronger magnetic field only makes the plasma more turbulent faster. And your fantasies of being the first to put electricity on the grid? At best you are a pathetic joke.

MIT & me, are we mutual jokes to each other?
Just like ITER and the Wendelstein 7X this will not work!

It is very difficult to make a working nuclear fusion reactor on earth if you just don’t want to study the magnetic properties of electrons while you try to contain the plasma with magnetic fields. Oh the physics imbeciles and idiots think they understand plasma? They even do not understand why the solar corona is so hot and if year in year out I say that magnetic fields accelerate particles with a net magnetic charge, the idiots and imbeciles just neglect it because they are idiots and imbeciles.

The third video is about a truly Hercules task: Making a realistic model of the sun so that can run in computer simulations… If humanity is still around 10 thousand years from now may be they have figured it out but the sun is such a complicated thing it just cannot be understood in a couple of decades. There is so much about the sun that is hard to understand. For example a number of years ago using the idea that electrons are magnetic monopoles, it thought that rotating plasma like in some tornado kind of structure is all you need to get extremely strong magnetic fields. But I never ever wrote down only one word in that direction. Anyway about a full year later I learned about the rotational differential for the sun: at the equator it spins much faster as it does on the poles. And that would definitely give rise to a lot of those tornade like structurs that must be below the sun spots.
Of course nothing happens because of ‘university people’ and at present day I do not give a shit any longer. I am 100% through with idiots and imbeciles like that. For me it only counts that I know, that I have figured out something and trying to communicate that to a bunch of overpaid highly absorbed in their giant ego’s idiots and imbeciles is a thing I just stopped doing. If it is MIT, ITER or Max Planck idiots and imbeciles, why should I care?

Ok, that was it for this post. If you are not related to a university or academia thanks for your attention. And to the university shitholes: please go fuck yourselves somewhere we don’t have to watch it.