Monthly Archives: February 2017

General Pythagoras theorem part 1: The 3D case.

Pythagoras stuff

A long time ago I found a very simple proof for the general theorem Pythagoras. At the time the general public had almost zero access to internet resources and in those long lost years I could not find out if my proof was found yes or no.

As memory serves, Descartes was the one that gave a proof for the 3D version of the Pythagorean theorem… (But I never did read the proof of Descartes.)

Two weeks back I was cleaning out my book closet so I could store more bottles of beer for the ripening process and I came across that old but never perfectly finished proof.

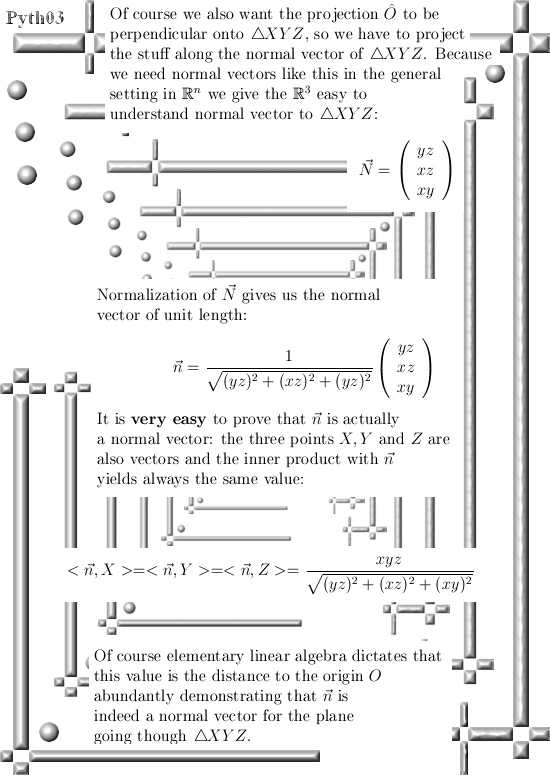
And it entered my mind again because it is fascinating that just by constructing that perfect normal vector, you make it of unit length, calculate a few higher dimensional volumes and voila:
There is you proof of the general theorem of Pythagoras.

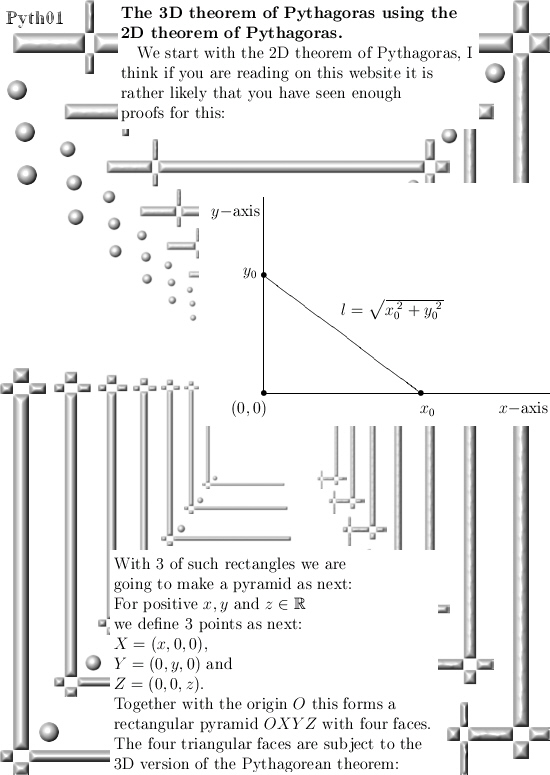
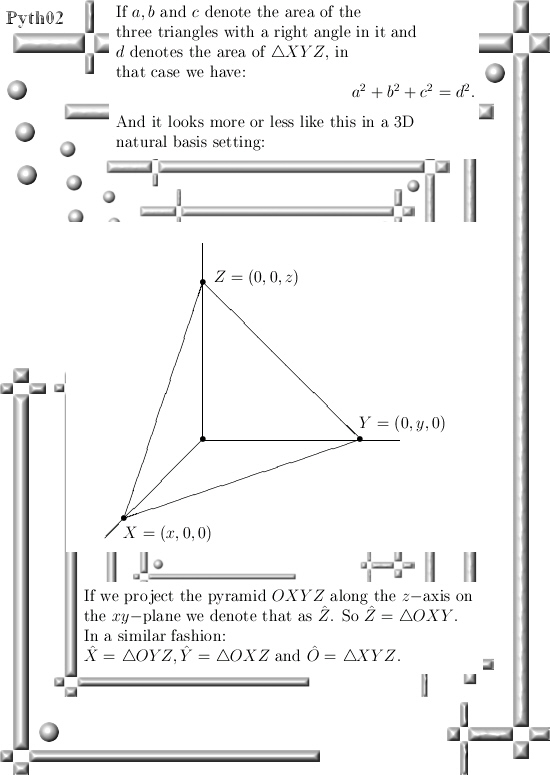
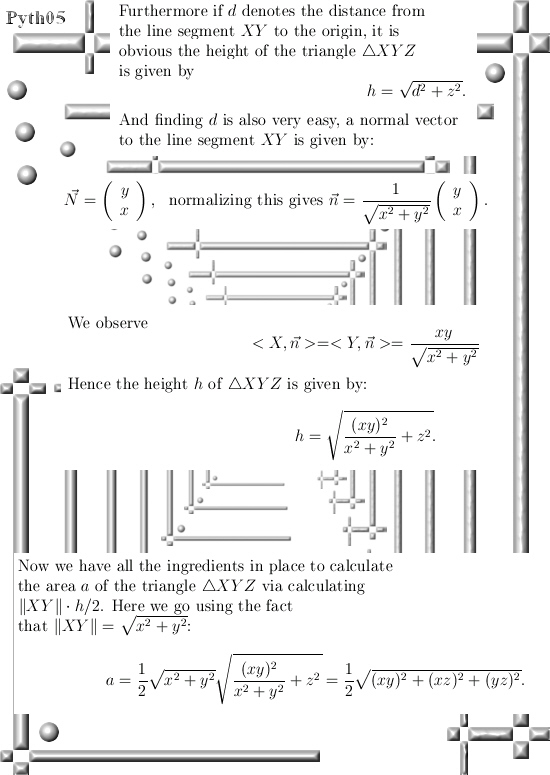
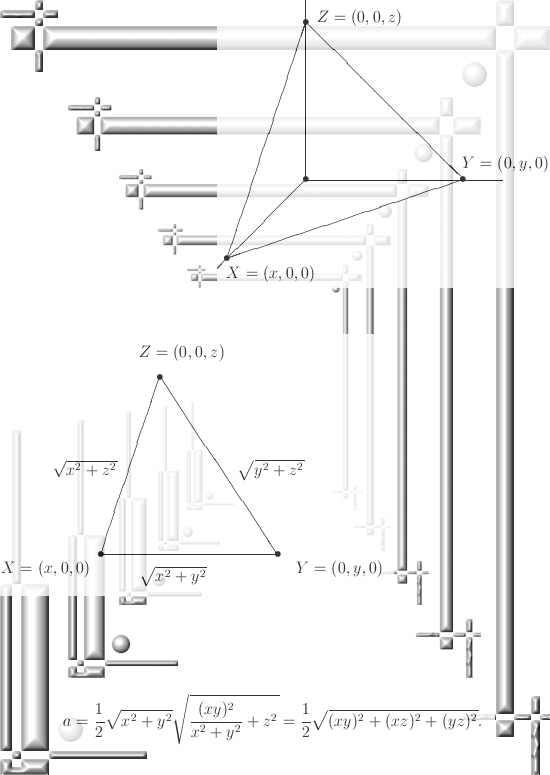
In this post we only look at the 3D example for the theorem of Pythagoras. But already here we use a normal vector together with the 2D theorem of Pythagoras in order to prove the result for 3D space.
Basically this is also precisely the way the proof works in all higher dimensions, ok ok the notations and ways of writing the stuff down is a bit more technical but if you understand the proof in this post you will immediately understand how the general proof works.

The general proof is based on the principle of natural induction, likely the reader is familiar with natural or mathematical induction because beside it’s elegance it is also easy to explain to first year students in exact sciences. Basically you prove some stuff for low values of n, say n = 2 or 3 for 2D and 3D space and after that you do the so called ‘induction step’ where you must show that if it holds for a particular value of n, the stuff you want to prove is also true for n + 1.

Here is a wiki on the subject: Mathematical induction
https://en.wikipedia.org/wiki/Mathematical_induction

__________

This post is five pictures long (size 550 x 775 as usual) so have fun reading it:

23Feb2017_generalized_Pythagoras_theorem01

23Feb2017_generalized_Pythagoras_theorem02

23Feb2017_generalized_Pythagoras_theorem03

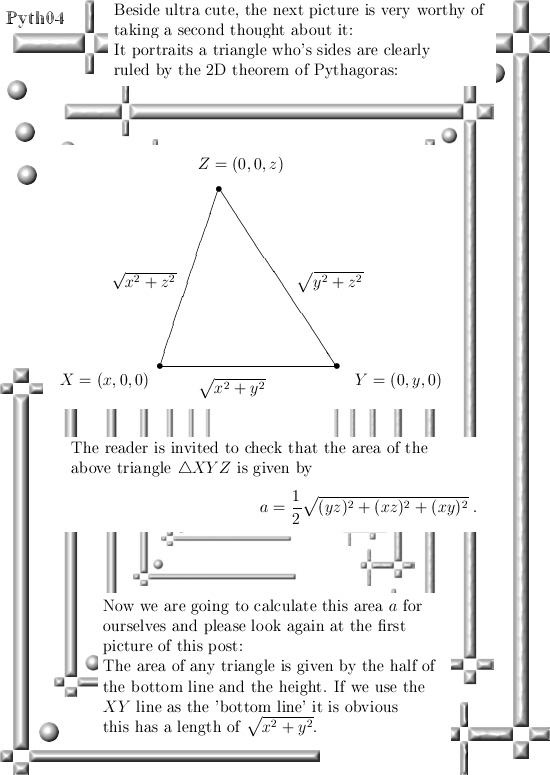
23Feb2017_generalized_Pythagoras_theorem04

23Feb2017_generalized_Pythagoras_theorem05

In the last line of the proof it is important to remark that both the length of XY is done with the 2D version of Pythagoras, but the height h of triangle XYZ is also done with the 2D version of Pythagoras. And so you get the 3D version of the famous Pythagoras theorem.

See you in the next post where it is all a bit more abstract and not slammed down to just two or three dimensions. Have a nice life or try to get one.

CERN stuff on super conductivity and a primer on the general theorem of Pythagoras.

Magnetism, Uncategorized

A few weeks back while cleaning out my book closet I came across that unfinished proof of the generalized theorem of Pythagoras that uses n-dimensional pyramids. (May be these are called simplexes and not pyramids, I still have to figure that out).

On the CERN stuff I can tell you I used a picture of CERN to explain a bit about super conductivity because at CERN they also run an experiment where they try to find magnetic monopoles…

It is now year number four where I constantly keep on telling that electrons are the long sought magnetic monopoles; electrons carry electrical charge, that is known in the scientific community, but they also carry two different magnetic charges.

As such electrons are much more like quarks that also carry electrical charge but also color charge, the fact that the electron carries only two magnetic  charges is the main explanation as why we only have electron pairs. If the official version of physics were a true description of reality, so electrons are truly magnetic dipoles, why only have electron pairs???

Super conductivity is caused by electron pairs, not by free electrons. A material can only become in a super conductivity state if first the so called Cooper electron pairs are formed.
If the official version is true and electrons are magnetic dipoles, in that case any applied magnetic field would have zero point zero influence on the formation of electron pairs.

That is crystal clear because all forces on the north pole of the electron would be canceled out by the forces on the south pole of the electron. Yet in practice, as not only CERN but the entire community of super conductivity research is telling us: In the presence of a too high magnetic field the material just not enters the state of super conductivity…

So you can cool your ass off, if magnetic fields are too high electron pair formation just does not set in. The next picture from CERN shows a bit of state space as where in super conductivity materials should get their super conductivity properties:

18Feb2017_critical_magnetic_field_and_super_conductivityLet me not put salt on every snail observed but the title should be ‘State space diagram of superconductors’ because ‘phase’ is related to 2D complex number stuff.

At last I would like to remark that although CERN is on a very expensive hunt for magnetic monopoles, they failed all of the time.
Now do CERN people talk about electrons being carriers of magnetic charge?
Come on; CERN people will fail all of the time.

On the other website we have reason number 45 as why electrons cannot be magnetic dipoles, as you have guessed it is about the above picture from CERN:

Reason 45: The critical magnetic threshold in super conductivity. 
http://kinkytshirts.nl/rootdirectory/just_some_math/monopole_magnetic_stuff02.htm#15Feb2017

__________

After having said my views on fantastic organizations like CERN, why not do some elementary math like for example the 3D theorem of Pythagoras?

As memory serves the math ideas in the picture below were found centuries ago, but I have to say I do not know much historical development of the math ideas involved.

But I do know that I found a very simple proof to the most general theorem of Pythagoras and that is what will be in the next post and may one more extra post to finish it off.

Here is the teaser picture for the next post (or may be two posts on this subject of generalizing the theorem of Pythagoras):

18Feb2017_intro_generalized_Pythagoras_theorem

The good thing about the last line of calculations is:

We need the millennia old 2D theorem of Pythagoras in order to prove the century old 3D theorem of Pythagoras…

I don’t know how far I will push this detail but if I find it back in my book closet may be I will write a tiny bit more. End of this post, see you around and try to get a nice life in case you never understood those electrons in the first place.

Till updates.

Debunking the most successful relation between theory and experiment in physics using electron magnetic charge.

Magnetism

May be it is best that you first take a look at the video given below, think about it for some time and, hopefully, arrive at the conclusion that at Fermilabs they have a lot of shallow thinkers.

With QED the physics people use that as an abbreviation for quantum electro dynamics, inside theories like that they sometimes use a so called ‘coupling constant’. The physics professors think they have found a perfect relation between the theoretical value of this coupling constant and experimental evidence.

This coupling constant relates the magnetic properties of the electron to the so called Bohr magneton. The Bohr magneton is related to the mass of the electron pair and as such is related to a magnetic dipole.

Anyway the video showing a guy named Dr. Don Lincoln has all the hallmarks for ‘shallow and easy thinking’ that is so pregnant through all of physics; just do some bla bla bla before an audience and actually come away with it. Here it is:

QED: Experimental evidence.

Now from the get go of the discovery of electron spin it was known that the large magnetic properties of the electron could not be explained via a spinning electron; even if all electrical charge was concentrated on the equator of the electron it should spin with a large multiple of the speed of light.

An important conclusion we can draw from that is: the actual spinning of an electron is more or less insignificant.

Now the measurement of the magnetic dipole moment of the electron was not done via a measurement of the magnetic dipole moment of an electron but only via year on year making many measurements of the frequency that those electrons did send out as electro-magnetic radiation.

It is well known that electrons send em-radiation when they get accelerated, this is a very general principle on all levels of the em-spectrum. Electrons always behave the same whatever frequency they oscillate.

So if electron magnetic properties cannot be explained via the actual rotation of an electron, why do the shallow thinkers as Don Lincoln always portrait it this way? Here is what the idiots show the public:

13-02-2017_Dr_Don_Lincoln_idiot_explanation

Yes they compare it to a gyroscope…

Now congratulations with your stupidity my dear Fermilab Dr. Don Loncoln; usually electrons do not spin faster than the speed of light.

If you come up with explanations like this, it is very clear you do not understand how electro-magnetic radiation is crafted in the first place. It has to do with both an electrical charge and a magnetic charge getting accelerated. The important thing to notice is the localization of both charges on the electron itself…

All that talk of electrons being magnetic dipoles is nonsense.

__________

From the viewpoint of psychology, the idea that physics professors have about the accuracy of the magnetic dipole moment of the electron is of course a big big hinder for accepting that electrons carry two possible magnetic charges: a north charge and a south charge.

Here is the source of their smirks, laughs and arrogant behavior:

13-02-2017_just_a_coupling_constantBut this measurement is only based on measuring frequencies of em-radiation.

Yet electrical fields can also accelerate electrons and oscillating electrical fields can also produce em-radiation from the electrons…

For the time being lets leave it with that; imbeciles that bring up stuff spinning above the speed of light while waiving away reality are classified as shallow or pseudo scientists.

And at Fermilabs, USA based, they have plenty of those people.
Till updates.

Simple statistics on the video of the oversight of the Stern-Gerlach experiment + Dwave qubits (quantum bits) explained.

Magnetism

Exactly one month ago I posted the update about the historical oversight on the Stern-Gerlach experiment from 1921. This experiment is just so confusing; how can a magnetic field split a beam of electrons in two parts?
If electrons are really magnetic dipoles, this should hot happen.
But it happens, hence I jumped to the conclusion electrons are beside electric monopoles also magnetic monopoles. As such they carry two magnetic charges known as north and south.

The video with the historical oversight had 1222 views on 03 Jan 2017, that would amount for about 9 views a day. This is very little if you compare that, for example, if Miley Cyrus brings out another ass shaking video but hey this was about an experiment in physics done about one century ago.

Right now the video has 1702 views and that means it has about 19 to 20 views a day since 03 Jan.
So the daily number of views has doubled but it is only 10 views extra a day.

But ok ok, I still accept it would be a long long battle; if there are truly about 100 thousand physics professors really thinking that electrons are magnetic dipoles because some fancy math says it is so, stuff has turned into dogma.
When I found the magnetic charge solution for myself I strongly remember asking myself:
BUT ELECTRONS ARE MAGNETIC DIPOLES, IS THAT RIGHT???

And there are some problems with the official version: The only thing that says electrons are magnetic dipoles is the Gauss law for magnetism. Tiny problem: electrons were discovered much time later…

Anyway I still advertise viewing the Stern-Gerlach experiment oversight because it is a treasure trove of not only historical facts but it also rings home that people like Albert Einstein, Niels Bohr, Erwin Schrödinger, Wolfgang Pauli etc etc just had NO CLUE WHATSOEVER on the fundamental importance of the outcome of the Stern-Gerlach experiment.

So once more the video:

The Stern-Gerlach Experiment And The Discovery Of Electron Spin – Sandip Pakvasa [2016]

The great thing about electrons having two magnetic charges it that you understand so much stuff from nature on a far deeper level. That is very rewarding and you can compare that for example to the discovery of the nucleus of the atom.

Now the title of this post says ‘Dwave qubits explained’ but if I would do that I would have to keep up a long story as why the formation electron pairs are needed for super conductivity (electron pairs are a north and a south charge together more or less magnetically neutral ensuring the super conductivity) while unpaired electrons are not neutral in the magnetic sense.

And so on and so on.

No, let me only post a picture from Nature, the famous Nature scientific outlet is somewhere I can never publish because they have so called ‘peer review’. Of course ‘peer review’ will never allow for crazy ideas that say electrons carry two different magnetic charges…

That is why university people and me will never be friends; we just do not speak the same language.

Here is the picture from the Nature outlet:

02-02-2017_Dwave_qubit

Picture source:
Figure 1: Superconducting flux qubit.
http://www.nature.com/nature/journal/v473/n7346/fig_tab/nature10012_F1.html

Dwave qubits are macroscopic objects, they are not small quantum systems but as you see in the picture above the folks from Dwave computer have succeeded into generating two electrical currents that go in opposite directions.

Ok ok, let me share just one simple to understand detail:

The two currents are unpaired electrons, although Dwave computers use super conductivity unpaired electrons do not follow the stream of super conductivity…

So after initialization, the two currents will die out.
I wonder if the people at Dwave are aware of this line of reasoning.

Let’s leave it with that, have a nice life or try to get one & till updates.