For me it was a strange experience to construct a square matrix and if you take the determinant of the thing the lower dimensional volume of some other thing comes out. In this post I will calculate the length of a 3D vector using the determinant of a 3×3 matrix.
Now why was this a strange experience? Well from day one in the lectures on linear algebra you are thought that the determinant of say a 3×3 matrix always returns the 3D volume of the parallelepiped that is spanned by the three columns of that matrix.
But it is all relative easy to understand: Suppose I have some vector A in three dimensional space. I put this vector in the first column of a 3×3 matrix. After I add two more columns that are both perpendicular to each other and to A. After that I normalize the two added columns to one. And if I now take the determinant you get the length of the first column.
That calculation is actually an example below in the pictures.

Well you can argue that this is a horrible complicated way to calculate the length of a vector but it works with all parallelepiped in all dimensions. You can always make a non-square matrix, say an nxd matrix with n rows and d columns square. Such a nxd matrix can always be viewed as some parallelepiped if it doesn’t have too many columns. So d must never exceed n because that is not a parallelepiped thing.

Orthogonal matrices. In linear algebra the name orthogonal matrix is a bit strange. It is more then the columns being orthogonal to each other; the columns must also be normalized. Ok ok there are reasons that inside linear algebra it is named orthogonal because if you name it an orthonormal matrix it now more clear that norms must be one but then it is more vague that the columns are perpendicular. So an orthogonalnormalized matrix would be a better name but in itself that is a very strange word and people might thing weird things about math people.
Anyway loose from the historical development of linear algebra, I would like to introduce the concept of perpendicular matrices where the columns are not normalized but perpendicular to each other. In that post we will always have some non-square matrix A and we add perpendicular columns until we have a square matrix.

Another thing I would like to remark is that I always prefer to give some good examples and try not to be too technical. So I give a detailed example of a five dimensional vector and how to make a 5×5 matrix from that who’s determinant is the length of our starting 5D vector.
I hope that is much more readable compared to some highly technical writing that is hard to read in the first place and the key idea’s are hard to find because it is all so hardcore.

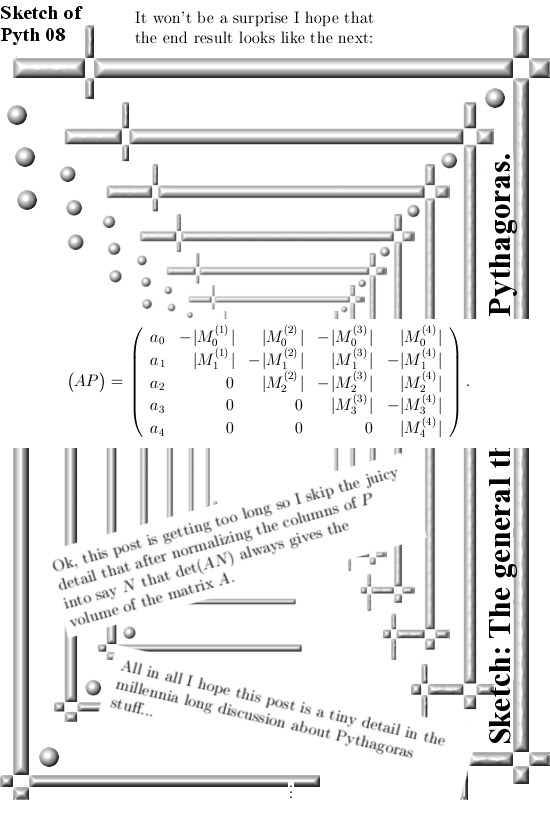
This small series of posts on the Pythagoras stuff was motivated by a pdf from Charles Frohman, you can find downloads in previous posts, and he proves what he names the ‘full’ theorem of Pythagoras via calculating the determinant of A^tA (here A^t represents the transpose of A) in terms of a bunch of minors of A.
A disadvantage of my method is that it is not that transparant as why we end up with that bunch of minors of A. On the other hand the adding of perpendicular columns is just so cute from the mathematical point of view that it is good to compose this post about it.

The post is eight pictures long so after a few days of thinking you can start to understand why this expansion of columns is say ‘mathematical beautiful’ where of course I will not define what ‘math beauty’ is because beauty is not a mathmatical thing. Here we go:

Inside linear algebra you could also name this the theorem of the marching minors. But hey it is time to split and see you in the next post.