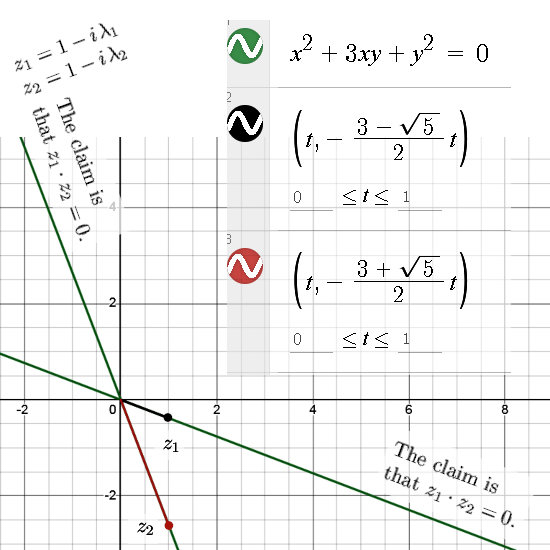
This is a horrible simple post, after all for the complex numbers ruled by i^2 = -1 + 3i all you have to do is look where the determinant of the matrix representaitons equals zero.
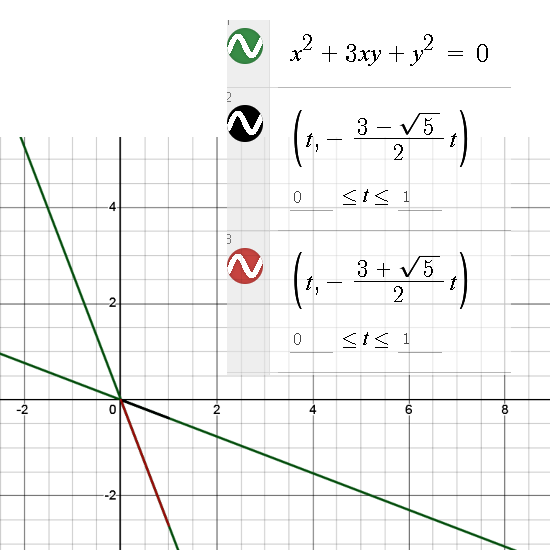
Well yes that is what we do, at present day there is that cute package or applet (in the past that was a so called computer program, why is all that kind of stuff an “applet” nowadays?) called DESMOS. With DESMOS the two lines that make up the set of non-invertibles is easy to graph.
These two lines are interesting because they are the asymptotes of all those hyperboles in this space, anyway those hyperboles that can be written as det(z) = constant. Furthermore the two lines where det(z) = 0 separate the parts of this complex plane where det(z) > 0 from the parts where det(z) < 0.

I took the opportunity to introduce a more comprehensive notation to denote such spaces of 2D complex and split complex numbers. I wrote it much more as a set like in set theory and it includes the ‘rule’ for the imaginary component.

For readers who are new to this website and don’t have a clue what ‘hyperbolic’ or ‘elliptical’ 2D complex numbers are, it is all basically rather simple:
These numbers are complex because i^2 = -1 + something, in the case of this post it is i^2 = -1 + 3i. These 2D complex numbers have matrix representations and the determinant of these matrices are constant along certain hyperboles. The case det(z) = 1 is very interesting for any of such a complex plane because that is a multiplicative group. Just like the unit circle in the standard or ordinary complex plane is a multiplicative group.

All in all this post has five pictures of size 550×1200 pixels and an additional two figures from graphs from the DESMOS applet.

For me it was funny to write some ‘high school math’ with just a few parabole kind of stuff in it. During the writing of this post I came across the idea of making a matrix representation of all that conjugating stuff, as such I found a beautiful but still extremely simple way to find the direction of the number tau in a particular space. The great thing is that this time it works in all dimensions so not only the 2D complex numbers but likely much much more.
Lets try to upload my post to the internet and may I thank you for your attention.