A bit like in the spirit of Sophus Lie lately I was thinking “Is there another way of finding those tangets at the number 1?”. To focus the mind, if you have an exponential circle or higher dimensional curve, the tangent at 1 is into the direction of the logarithm you want to find.
In the case of 2D and 3D numbers I always want to know the logarithm of imaginary units. A bit more advanced as what all started a long time ago: e^it = cos t + i sin t.
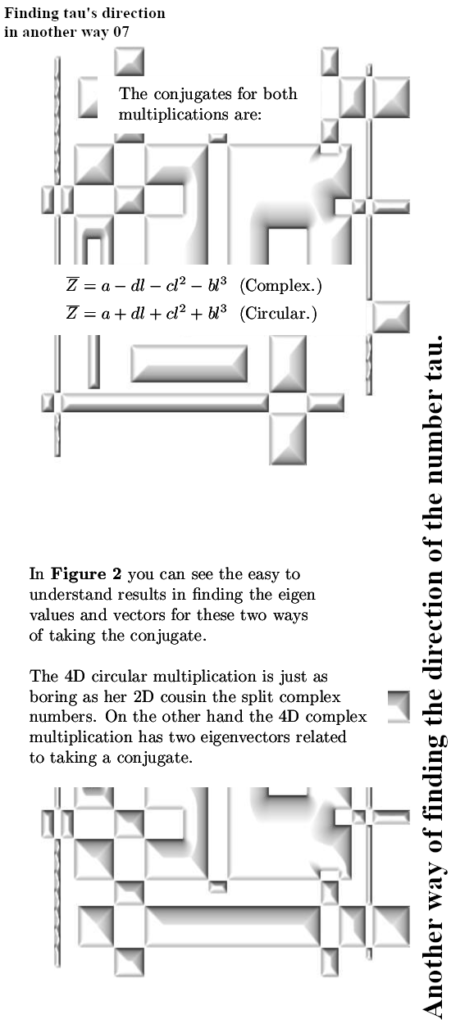
An important feature of those numbers tau that are the sought logs is that taking the conjugate always the negative returns. Just like the in the complex plane the conjugate of i is –i.

The idea is easy to understand: The proces of taking a conjugate of some number is also a linear transformation. These transformations have very simple matrices and there all you do is try to find the eigenvector that comes with eigenvalue -1.
The idea basically is that tau must like in the direction of that eigenvector.

That is what we are going to do in this post, I will give six examples of the matrices that represent the conjugation of a number. And we’ll look at the eigenvectors associated with eigenvalue -1.

At the end I give two examples for 4D numbers and on the one hand you see it is getten a bit more difficult over there. You can get multiple eigenvectors each having the eigenvalue -1. Here this is the case with the complex 4D numbers while their ‘split complex’ version or the circular 4D numbers have not.
Now all in all there are six examples in this post and each is a number set on it’s own. So you must understand them a little bit.
The 2D numbers we look at will be the standard complex plane we all know and love, the elliptic and hyperbolic variants from lately. After that the two main systems for 3D numbers, the complex and circular versions. At last the two 4D multiplications and how to take the conjugate on those spaces.

The post itself is seven pictures long and there are two additional pictures that proudly carry the names “Figure 1” and “Figure 2”. What more do you want? Ok, lets hang in the pictures:

Years ago it dawned on me that the numbers tau in higher dimensional spaces always come in linear combinations of pairs of imaginary units. That clearly emerged from all those calculations I made as say the 7D circular numbers. At the time I never had a simple thing to explain why it always had to be this pair stuff.
So that is one of the reasons to post this simple eigen vector problem: Now I have a very simple so called eigen value problem and if the dimensions grow the solution always come in pairs…

That was it for this post, likely the next post is upon so called ‘frustrated’ magnetism because the lady in the video explains the importance of understand energy when it comes to magnetism. After that may be a new math post on matrix representations of the actual conjugates, so that’s very different from this post that is about the matrices from the process of taking a conjugate…
As always thanks for your attention.