With a new number tau (see previous post) there is always a log of an suitable imaginary unit found, but that does not mean you have a parametrization instantly. And with ‘suitable’ I mean the determinant of the imaginary unit must be one because I always want to make some complex exponential, in this case a complex exponential hyperbole.
The post is relatively short, I always try to write short posts and I always fail fail and fail in that. But now it’s only four pictures long so this comes close to a tiktok version of my ususal math postings. By the way it has nothing to do with this post, but do you like tiktok? I don’t like it very much, it is more for people that have a bit different mindset compared to the way my old brain works…
In this post I first neatly write down the parametrization using the sinh and cosh to express the two coordinate functions. And after that I more or less express it all as much as possible into the two eigenvalues of our beloved imaginary unit i that rules this plane via: i^2 = -1 + 3i.
May be you have never thought about imaginary units as having eigen values themselves. In that case I invite you to calculate the eigenvalues of the ordinary numbers z from the complex plane. You know that plane that is ruled by an imaginary unit i via the rule: i^2 = -1. You will find a very interesting answer and of course after that you wonder WTF are the eigen vectors?

But let us not digress and enjoy the beauty of a complex exponential that is a hyperbole in this case. Here we go:

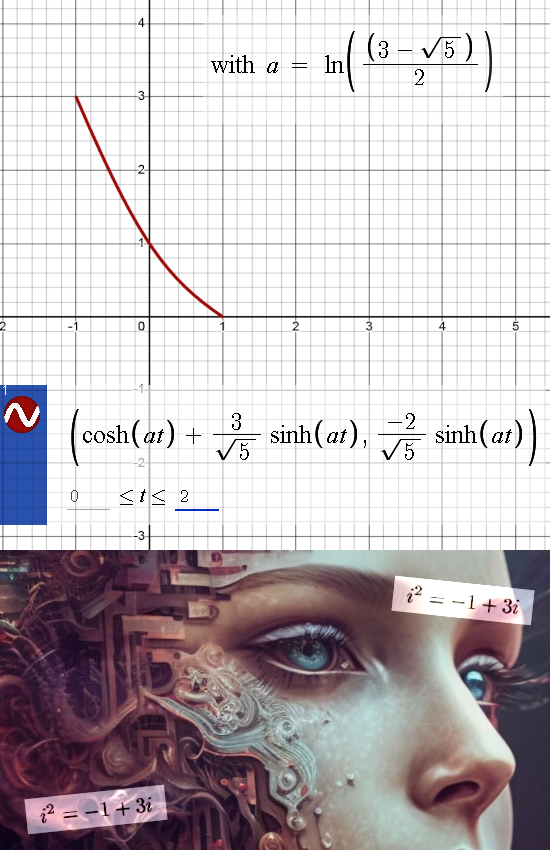
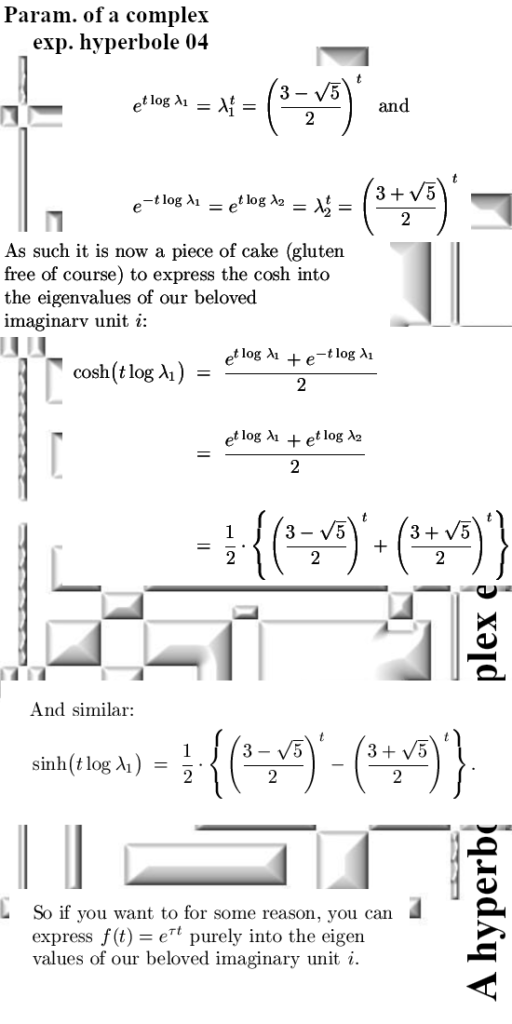
I am sorry for those bad looking accolades, it is some small fault in the Latex math package or some other old computer feature. You see it in much more texts written in Latex; the { and the } are just not presented properly.
That was it for this post, as always thanks for your attention.