I am rather satisfied with the approach of doing the same stuff on the diverse complex spaces. In this case the 2D complex plane and the 3D & 4D complex number systems. By doing it this way it is right in your face: a lot of stuff from the complex plane can easily be copied to higher dimensional complex numbers. Without doubt if you would ask a professional math professor about 3D or higher dimensional complex numbers likely you get a giant batagalization process to swallow; 3D complex numbers are so far fetched and/or exotic that it falls outside the realm of standard mathematics. “Otherwise we would have used them since centuries and we don’t”. Or words of similar phrasing that dimishes any possible importance.

But I have done the directional derivative, the factorization of the Laplacian with Wirtinger derivatives and now we are going to do the total differential precisely as you should expect from an expansion of the century old complex plane. There is nothing exotic or ‘weird’ about it, the only thing that is weird are the professional math professors. But I have given up upon those people years ago, so why talk about them?

In the day to day practice it is a common convention to use so called straight d‘s to denote differentiation if you have only one variable. Like in a real valued function f(x) on the real line, you can write df/dx for the derivative of such a function. If there are more then one variable the convention is to use those curly d’s to denote it is partial differentiation with respect to a particular variable. So for example on the complex plane the complex variable z = x + iy and as such df/dz is the accepted notation while for differentiation with respect to x and y you are supposed to write it with the curly d notation. This practice is only there when it comes to differentiation, the opposite thing is integration and there only straight d‘s are used. If in the complex plane you are integrating with respect to the real component x you are supposed to use the dx notation and not the curly stuff.
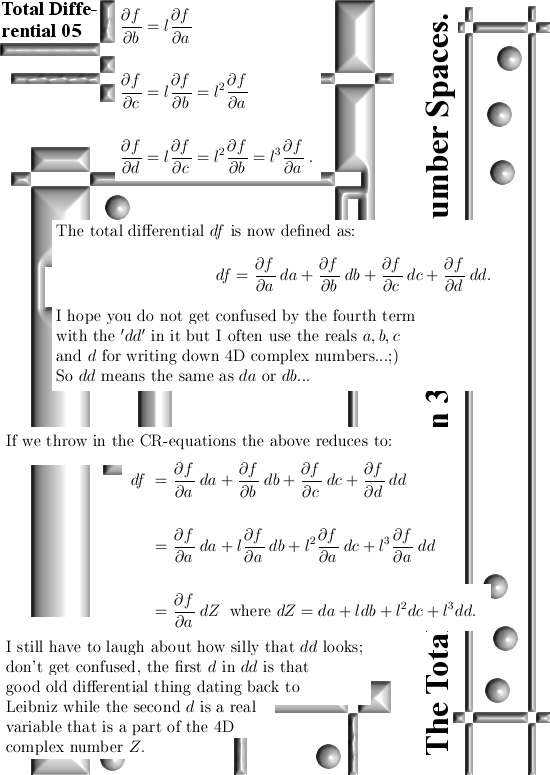
Well I thought I had all of the notation stuff perfectly figured out, oh oh how ultrasmart I was… Am I writing down the stuff for the 4D complex numbers and I came across the odd expression of dd. I hope it does not confuse you, in the 4D complex number system I always write the four dimensional numbers as Z = a + bl + cl^2 + dl^3 (the fourth power of the imaginary unit l must be -1, that is l^4 = -1, because that defines the behavior of the 4D complex numbers) so inside Z there is a real variable denoted as d. I hope this lifts the possible confusion when you read dd…

More on the common convention: In the post on the factorization of the Laplacian with Wirtinger derivatives I said nothing about it. But in case you never heard about the Wirtinger stuff and looked it up in some wiki’s or whatever what, Wirtinger derivatives are often denoted with the curly d‘s so why is that? That is because Wirtinger derivatives are often used in the study of multi-variable complex analysis. And once more that is just standard common convention: only if there is one variable you can use a straight d. If there are more variable you are supposed to write it with the curly version…

At last I want to remark that the post on the factorization of the Laplacian got a bit long: in the end I needed 15 pictures to publish the text and I worried a bit that it was just too long for the attention span of the average human. In the present years there is just so much stuff to follow, for most people it is a strange thing to concentrate on a piece of math for let’s say three hours. But learning new math is not an easy thing: in your brain all kind of new connections need to be formed and beside a few hours of time that also needs sleep to consolidate those new formed connections. Learning math is not a thing of just spending half an hour, often you need days or weeks or even longer.

This post is seven pictures long, have fun reading it and if you get to tired and need a bit of sleep please notice that is only natural: the newly formed connetions in your brain need a good night sleep.

Here we go with the seven pictures:

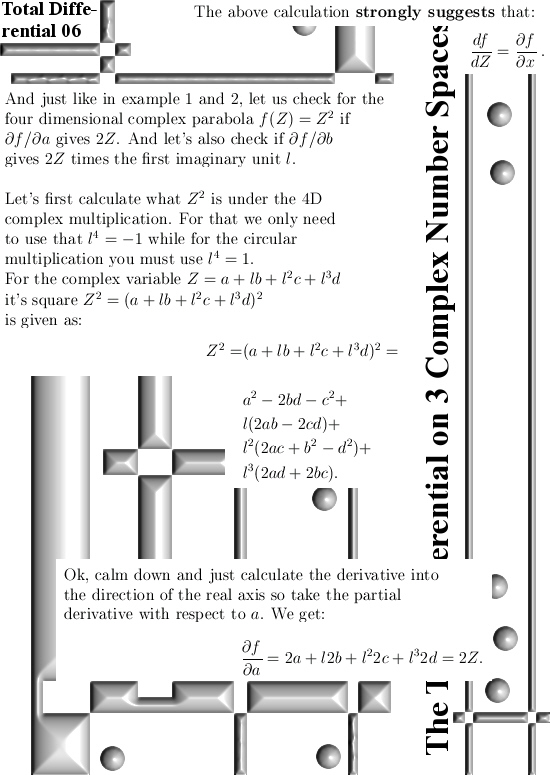
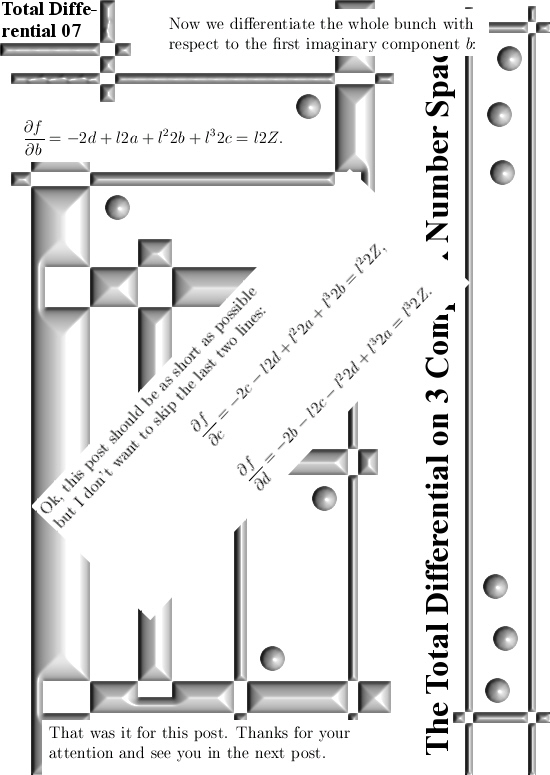
Yes, that’s it for this post. Sleep well and think well & see you in the next post. (And oh oh oh a professional math professor for the first time in his or her life they calculate the square Z^2 of a four dimensional complex number; how many hours of sleep they need to recover from that expericence?)
See ya in the next post.