For a couple of years I have a few pdf files in my possession written by other people about the subject of higher dimensional complex and circular numbers. In the post we will take a look at the work of Shlomo Jacobi, the pdf is not written by him because Shlomo passed away before it was finished. It is about the 3D complex numbers so it is about the main subject of this website.

Let me start with a link to the preprint archive:

On a novel 3D hypercomplex number system

Link used: http://search.arxiv.org:8081/paper.jsp?r=1509.01459&qid=1603841443251ler_nCnN_1477984027&qs=Shlomo+Jacobi&in=math

Weirdly enough if you search for ‘3D hypercomplex number’ the above pdf does not pop up at all at the preprint archive. But via his name (Shlomo Jacobi) I could find it back. Over the years I have found three other people who have written about complex numbers beyond the 2D complex plane. I consider the work of Mr. Jacobi to be the best so I start with that one. So now we are with four; four people who have looked at stuff like 3D complex numbers. One thing is directly curious: None of them is a math professional, not even a high school teacher or something like that. I think that when you are a professional math professor and you start investigating higher dimensional complex numbers; you colleagues will laugh about it because ‘they do not exist’. And in that manner it are the universities themselves that ensure they are stupid and they stay stupid. There are some theorems out there that say a 3D complex field is not possible. That is easy to check, but the math professionals make the mistake that they think 3D complex numbers are not possible. But no, the 2-4-8 theorem of say Hurwitz say only a field is not possible or it says the extension of 2D to 3D is not possible. That’s all true but it never says 3D complex numbers are not possible…

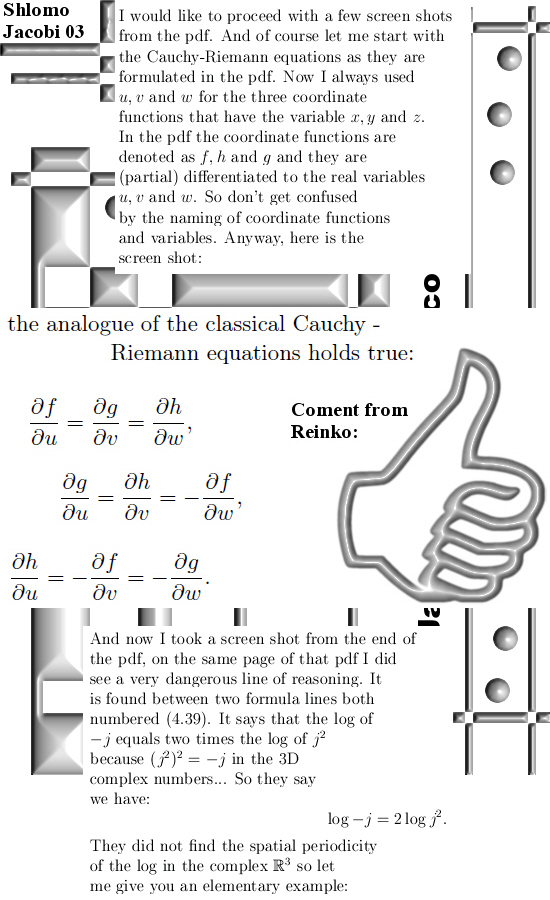
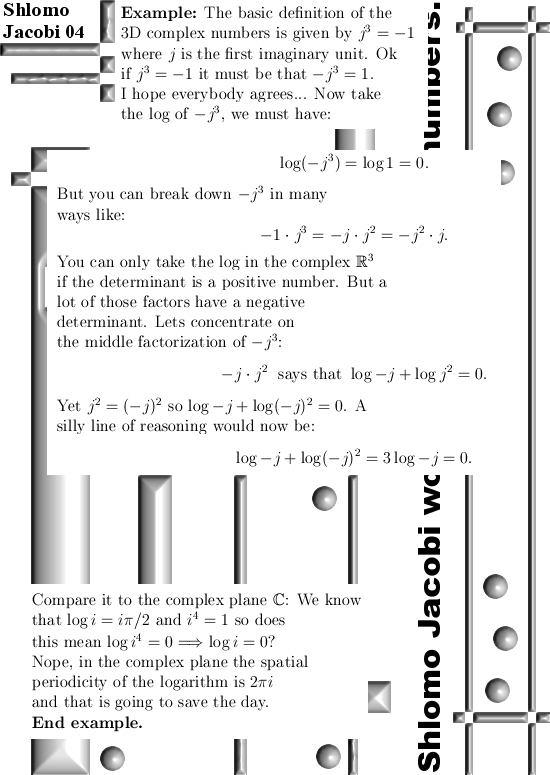
Because Shlomo Jacobi passed away an unknown part of the pdf is written by someone else. So for me it is impossible to estimate what was found by Shlomo but is left out of the pdf. For example Shlomo did find the Cauchy-Riemann equations for the 3D complex numbers but it is only in an epilogue at the end of the pdf.

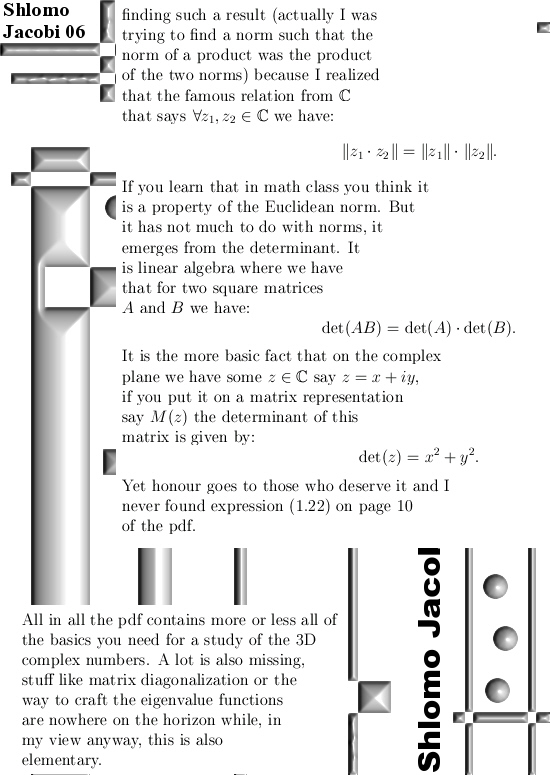
The content of the pdf can be used for a basic introduction into the 3D complex numbers. It’s content is more or less the ‘algebra approach’ to 3D complex numbers while I directly and instantly went into the ‘analysis approach’ bcause I do not like algebra that much. The pdf contains all the basic stuff: definition of a 3D complex number, the inverse, the matrix representation and stuff he names ‘invariant spaces’. Invariant spaces are the two sets of 3D complex numbers that make up all the non-invertible numbers. Mr. Jacobi understands the concept of divisors of zero (a typical algebra thing that I do like) and he correctly indentifies them in his system of ‘novel hypercomplex numbers’. There is a rudimentary approach towards analysis found in the pdf; Mr. Jacobi defines three power series named sin1, sin2 and sin3 . I remember I looked into stuff like that myself and somewhere on this website it must be filed under ‘curves of grace’.

A detail that is a bit strange is the next: Mr. Jacobi found the exponential circle too. He litarally names it ‘exponential circle’ just like I do. And circles always have a center, they have a midpoint and guess how he names that center? It is the number alpha…

Because Mr. Jacobi found the exponential circle I applaud him long and hard and because he named it’s center the number alpha, at the end I included a more or less new Euler identity based on a very simple property of the important number alpha: If you square alpha it does not change. Just like the square of 1 is 1 and the square of 0 is 0. Actually ‘new’ identity is about five years old, but in the science of math that is a fresh result.

The content of this post is seven pictures long, please read the pdf first and I hope that the mathematical parts of your brain have fun digesting it all. Most pictures are of the standard size of 550×775 pixels.

Ok ok, may be you need to turn this into exponential circles first in order to craft the proof that a human brain could understand. And I am rolling from laughter from one side of the room to the other side; how likely is it that professional math professors will find just one exponential circle let alone higher dimensional curves?

I have to laugh hard; that is a very unlikely thing.

End of this post, see you around & see if I can get the above stuff online.