I am going to make this update on the other website so in about one week you can check it out on page 4 of the 3D complex numbers. I admit I have been lazy the last month but now I have stopped smoking over three years my health is still improving so I am more exploring the environment with my bike while I can do that again…

Ha! At my worst about four years back I could only walk 100 to 125 steps and after that I needed to pause 3 to 4 minutes because I got camps in one of my legs. So it finally dawned on me I had to stop this nicotine addiction because the next phase would be a wheelchair combined with an oxygen mask and a tank of high pressured liquid oxygen on the back of my wheelchair.

Looking back I am glad I got so ill because without it I would never have managed to stop smoking those ridiculous amounts of cigarettes day in day out.

Sorry to bother you with my past health problems, this new teaser picture is rather funny and I hope also intriguing: I have crafted three coordinate functions x(t), y(t) and z(t) and if you differentiate them with respect to the time t you get a 3D square of the vector (x(t), y(t), z(t)).

So check it out for yourself; take the derivative of the three coordinate functions and see if you can get the three equations as on the bottom of the teaser picture…

The new update (on the other website) is ten pages long meaning it is 10 pictures of size 550 x 1100. Click on the teaser picture to land on the new update:

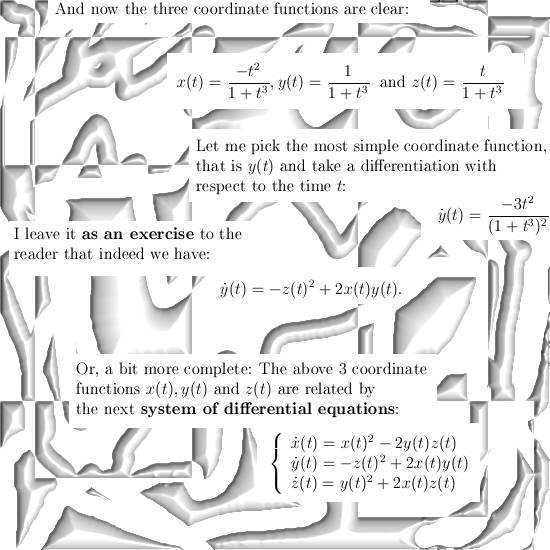For me it is just so cute: If you differentiate to time you get the square of the position you are in the 3D complex number system.

For use in the science of physics I do not think it is that important because real physical problems never rely on the coordinate system you use, but you never know…
For use in the science of math it is also not important because professional math professors still have not developed the cognitive capabilities of understanding 3D complex numbers.

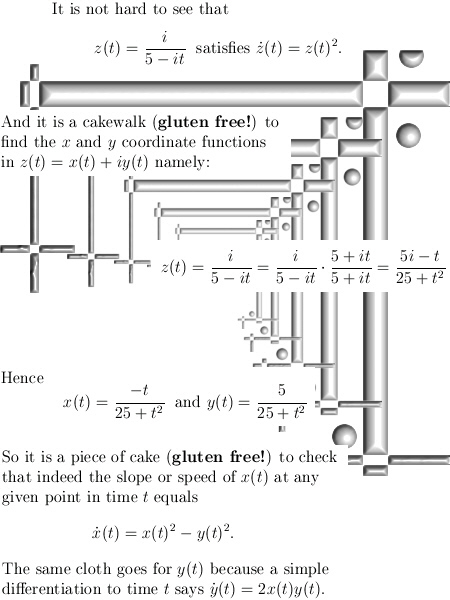
I also made a teaser picture for use on the other website, it is the same solution to the simple differential equation as above but this time I solved it inside the complex plane. Of course I could not use that on this website as the first teaser picture given the face we more or less always try to focus on the 3D complex & circular number systems…

Ok, end of this post.
And life, as usual life will go on.

Till updates.