This week I finally did put in the last details of the proof for the general theorem of Pythagoras. Now a long long time ago somewhere like in 1993 or1994 when I found this proof I could only find a very different proof in the official literature.
That proof worked with a matrix, I do not remember how it worked but the important feature is that this proof that used a matrix did not need a special coordinate system.
In the proof that I found I need the origin in the place where all lines, planes, hyper planes etc meet perpendicular so it is pretty natural to use the natural basis in n-dimensional real vector space.
The simplicity of this proof hangs on the construction of a normal vector to a hyper-plane and although I know this result for over two decades once more I was stunned about how easy this normal vector is to find and how easy it is to use the properties of this normal vector in proving the general theorem of Pythagoras.
Because after all; if you are given n + 1 points in n-dimensional space and you must prove something about the convex span of those n + 1 points, most of the time you just scratch your chin a bit, think a bit about it & never make any progress at all…
But using this easy to construct normal vector, instead of a difficult fog you have crystal clear skies over math paradise, what more should a reasonable person want???
In the year 2017 we have a much much better developed internet compared to the times when I originally did find my own version of a proof, but I did not research any of the outlets we have today like, for example, Google books.
If I can find a few good links I will update this post later.
This post is an additional 7 pictures to the previous post, each picture is as usual 550 x 775 pixels.
If you haven’t read the first post containing the first five pictures, please go here.
Once more: The surprising result is how easy to construct this normal vector is…
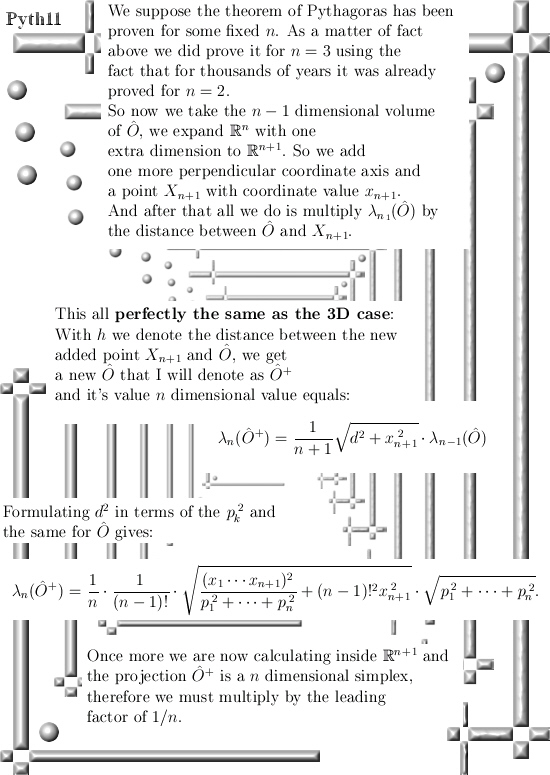
For myself speaking I am a little bit dissatisfied by notations like O with a hat and a + in the exponent, but I could not find a more easy notation so you simply must swallow that:
O hat lives in n-dimensional space while
O hat with the plus in the exponent lives in (n + 1)-dimensional space…
Ok, this is what I had more or less to say. If I can find a few good links I will post these later and if not see you around & try to get a nice life in case you don’t already have such a kind of life.