Ok ok, I admit instantly that the title of this post is way over the top but for once I allow myself a catchy title that has only limited resemblance to what this post is about. In this post, if I write the word computer I always mean a classical computer so not a quantum version of it.
In the previous post there is a video in from the ‘Infinite Series’ that serves as an introduction to the Shor algorithm; if this algorithm could be implemented into a quantum computer that would likely break internet security for a short while. Beside the fact that large prime numbers are used in standard classical encryption, it can also be done with elliptic curves.
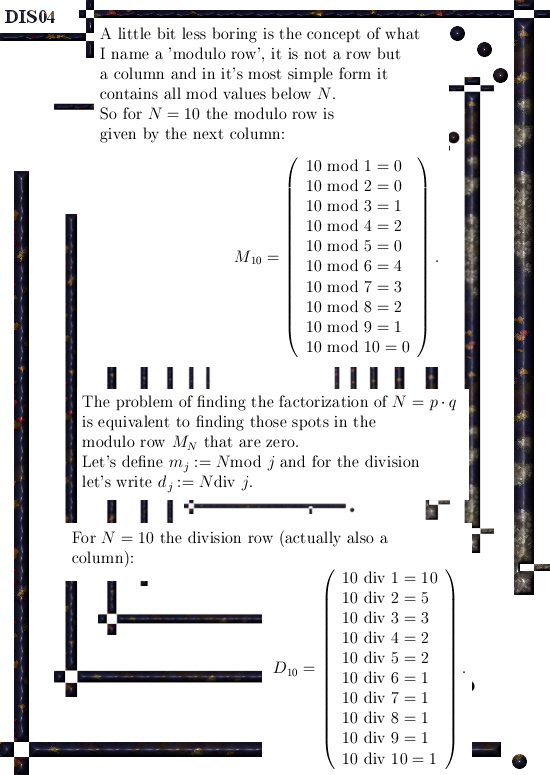
This post is about the principle of Jente, with a bit of luck you can find factors of large numbers using the principle of Jente. Counter intuitively the largest (prime) factor will be the easiest to find.
Now how did Jente find the principle of Jente?
Back in the time, end 1997 or begin 1998, we lived in a house without a garden and since I still smoked a lot of tobacco I always had a window open in my working room. Since this work room was next to the entry of the house, very often when the door to my room opened papers would fly from my desk because of wind going through the room.
There was this cute baby crawling around and one day she brought me back a piece of paper that had flown off my desk. And on that piece of paper was a little cute formula that read
m_{j+1} = m_j – d_j. So that is how this got the name the principle of Jente.
Lately Jente turned 21 years of age, she now lives temporary in Australia, and I decided to write this old stuff down as a kind of present for her. The principle of Jente is extremely easy to understand, but as far as I know mathematical reality this principle has not been exhausted very much by the entire math community over centuries of time.
What is missing in this post is a way to converge fast with high speed to one of the factors of one of those huge composite numbers the software engineers use for internet security. My gut feeling says that it should not be that hard but until now I have never found it. It might very well be that inside things like Diophante equations somewhere the solution to this problem of fast finding the largest prime factor is solved without the person who has done that being aware of it…
I tried to keep this post as short as possible so I scrapped a whole lot of stuff but it is still 15 pictures long (picture size as usual 550 x 775 pixels). A feature that I like very much is that I am using so called Harry Potter beans in order to explain as why the Jente principle works. I feel a bit proud on that because it is so simple you could explain that to elementary pupils in their highest years.
For myself speaking I also like this approach to finding prime factors because it is so different from all other ways, yet it has that underlying undeniable thing in it named the Jente principle. The most important detail in this post is the table with the diagonals in it.
If you understand that table and, for example, you can find another algorithm for quantum computers that solves that problem, you have found an alternative to the Shor algorithm…
Have fun reading it, take your time because it is not meant to be grasped in five minutes or so.

I hope you understand the fundamental problem still open after almost two decades:
You start with some number j, calculate m_j = N mod j and d_j = N div j.
Having these, the Jente principle guarantees you can find (j + k) mod N for all k > 0.
But, how oh how, do you converge towards a solution of
m_{j+k} = 0 mod (j+k) ?????
__________
The Shor algorithm: In the world of quantum computing we have the theoretical side where people just write down all kinds of elaborate scheme’s like the Shor algorithm and just as easy they throw in a lot of Hadamard gates that supposedly will bring a giant bunch of quantum bits into super position.
On the other hand you have people that actually try to build quantum computers.
As far as I know stuff, there is no way of bringing a lot of qbits into a nice super position or, for that matter, entangle them into a good initialization state in order to run your quantum software.
More info:
Hadamard transform
https://en.wikipedia.org/wiki/Hadamard_transform
Shor’s famous algorithm: Shor’s algorithm
https://en.wikipedia.org/wiki/Shor%27s_algorithm
Elliptic Curve Cryptography: a gentle introduction
http://andrea.corbellini.name/2015/05/17/elliptic-curve-cryptography-a-gentle-introduction/
__________
Ok, that was it. Don’f forget to pop open a few beers. Don’t believe all that nonsense that doctors are telling you like drinking less = good.
As far as I know reality, all people in my social environment that drink far too little beer always get killed in extremely violent events… 😉
Till updates.