This website is now about 3 years old, the first post was on 14 Nov 2015 and today I hang in with post number 100. That is a nice round number and this post is part 15 in the series known as the Basics for 4D complex numbers.
We are going to diagonalize all those matrix representations M(Z) we have for all 4D complex numbers Z. As a reader you are supposed to know what diagonalization of a matrix actually is, that is in most linear algebra courses so it is widely spread knowledge in the population.
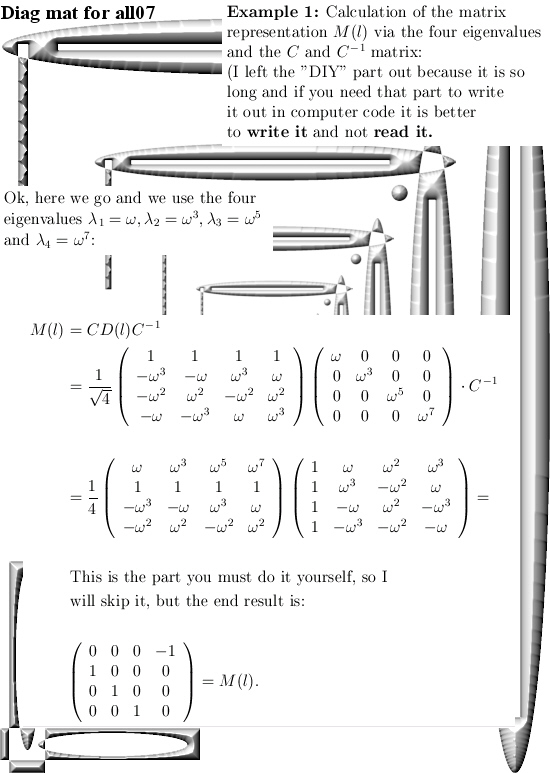
Now at the end of this nine pictures long post you can find how you can calculate the matrix representation for M(l) where l is the first imaginary unit in the 4D complex number system. And I understand that people will ask full of bewilderment, why do this in such a difficult way? That is a good question, but look a bit of the first parts where I gave some examples about how to calculate the number tau that was defined as log l. And one way of doing that was using the pull back map but with matrix diagonalization you have a general method that works in all dimensions.
Beside that this is an all inclusive approach when it comes to the dimension, in practice you can rely on internet applets that use commonly known linear algebra. Now if you are a computer programmer you can automate the process of diagonalization of a matrix. I am very bad in writing computer programs, but if you can write code in an environment where you can do symbolic calculus in your code, it would be handy if that is on such a level you can use the so called roots of unity from the complex plane. After all the eigenvalues you encounter in the 4D complex number system are always based on these roots of unity and the eigenvectors are too…
This post number 100 is 9 pictures long, as usual picture size is 550 x 775 pixels.
In the next post number 101 we will use this method to calculate the matrix representation of the number tau (that is the log of the first imaginary unit l).
Ok, here are the pictures:







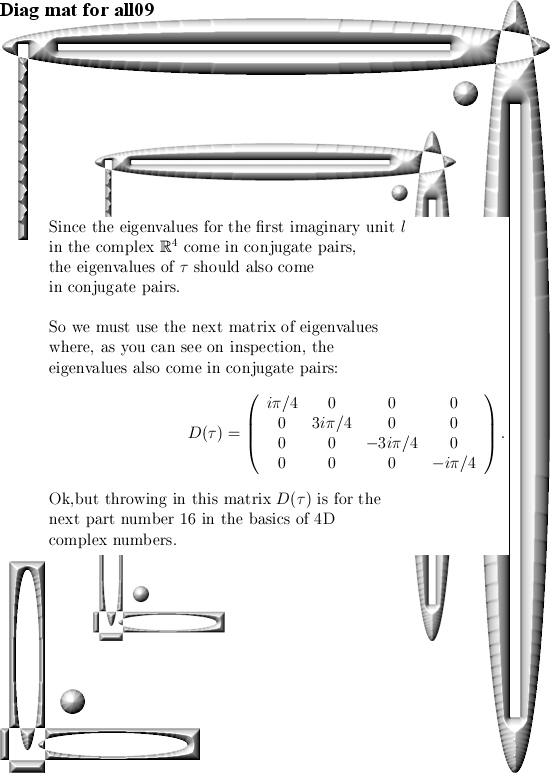
That´s it, in the next post we go further with the number tau and from the eigenvalues of tau calculate the matrix representation. So see you around.