In general it is rather hard to find non-invertible 4D complex numbers because the determinant is non-negative everywhere. Just try it yourself, write down just one 4D complex number that is non-zero and not invertible.

That is not an easy task, after some time you will find some but do you have all?

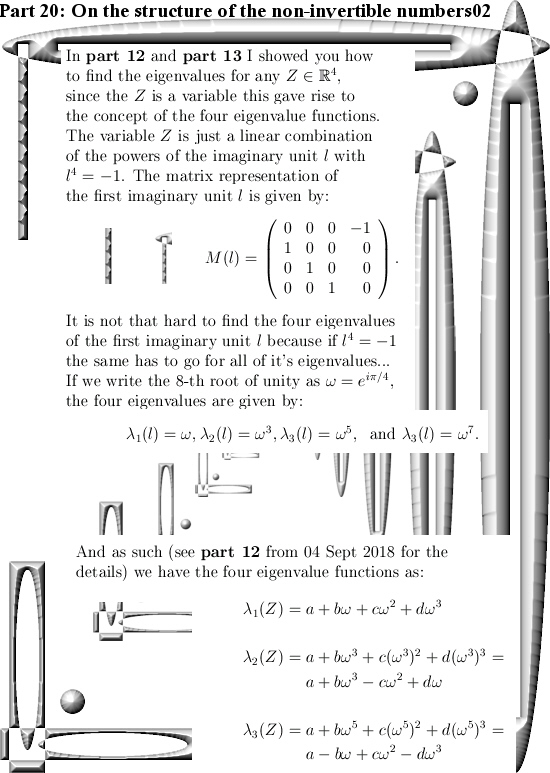
But if you understand the concept of the eigenvalues that every 4D complex number Z has, it is easy to understand that if a 4D complex number is non-invertible at least one of the eigenvalues must be zero.

In previous posts we already unearthed the four eigenvalue functions that return the four eigenvalues each 4D complex number has.

In this post we will try to find where these eigenvalue functions are zero.

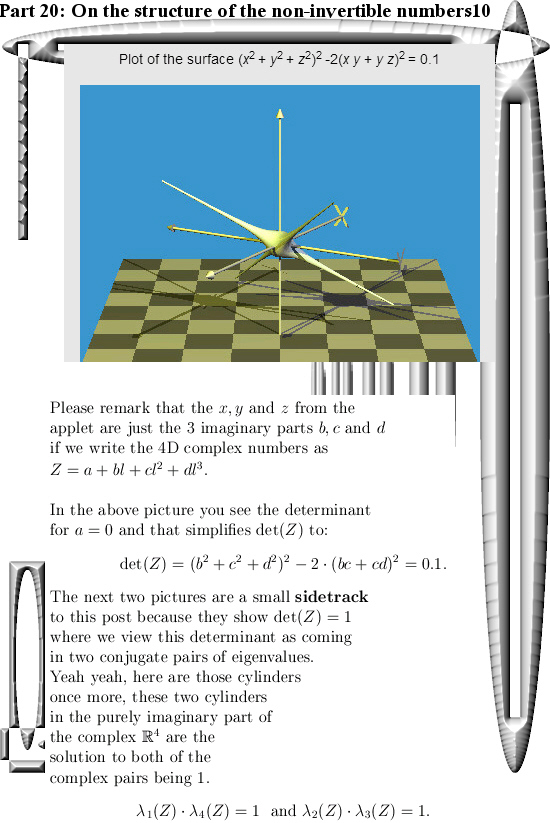
Since eigenvalue functions come in pairs whenever possible in the case of 4D complex numbers we only have two pairs of those eigenvalue functions.

Let’s stop the talking and just post the twelve pictures that make up part number 20 into the basics of the four dimensional complex numbers.

 

 

 

 

 

 

 

 

 

 

 

 

Ok, that was it for part 20 in the series that covers the basics of 4D complex numbers.

See you around my dear reader.