Monthly Archives: May 2019

3D numbers: Decomposition of all numbers into two non-invertible numbers.

3D complex numbers, Quantum mechanics

I got the idea for this post already a couple of years back but I shelved it because I would like to have some application for it. But I still haven’t found a killer application yet anyway I decided to write this rather simple post about the projections you get when you multiply any 3D complex and circular numbers with the number alpha. If you need a refreshment on the importance of the number alpha (or what it actually is) please use the search function of this website and search for ‘Seven properties of the number alpha’.

Now two months back I observed some guy in a video explaining the math you need for quantum physics (yes I have a very boring life) and he was explaining you also need projectors P such that P^2 = P meaning that if P is some measuring operator, if you measure it twice you get the same result. And ha, now I write this post down I realize I did not prove that for both operators in the pictures below so that is something you can do for yourself if you want that.

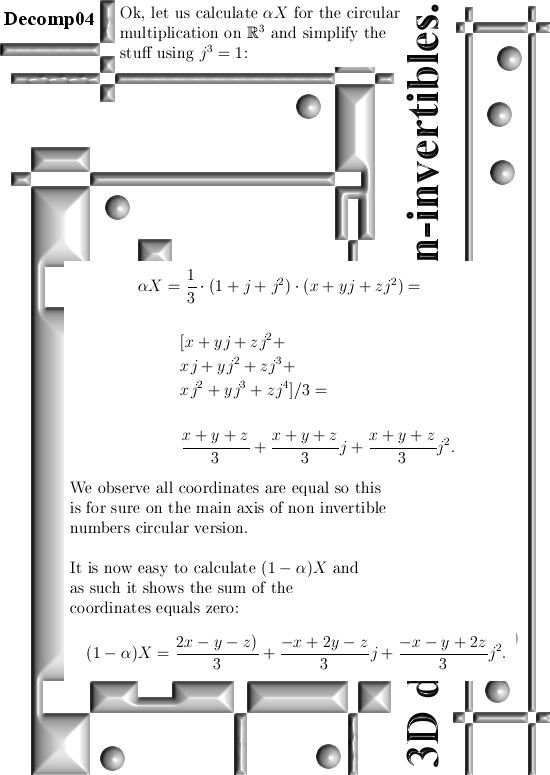
Basically it goes as next: Pick any 3D number X, circular or complex, and multiply it by the number alpha. The result is a number on the main axis of non-invertible numbers (and as such an entire 2D plane gets projected on each of the main axis non invertible numbers). The other operator is (1 – alpha) and if you multiply any 3D number X by that, it gets projected on the plane of non-invertible numbers (and as such a line gets projected on a point of that plane).

All in all it is very basic, but ha ha ha I am doing this stuff now for years on a row and may be for the average reader it is all not so basic. This post is easier to grasp if you understand the shape of the non-invertible numbers: it is a plane and perpendicular on that plane the main axis and both the plane and main axis go through zero. In this post I skipped all things eigenvalue, but in 3D space we have 3 eigenvalues per capita number so unlike in 4D space we cannot have eigenvalue pairs only. In 3D space it has to be different and that explains more or less the shape of the non-invertible numbers.

This post is five pictures long, as usual all 550×775 pixels and I really hope it is not that hardcore this time.











That is caused by the eigenvalues of a number.

Before we split, on the other website I posted reason number 73 as why electrons cannot be magnetic dipoles. I was that lucky to come across an old 1971 translation of some stuff of the Goudsmit & Uhlenbeck guys. I always suspected there had been some very sloppy physics going on back in the time at the local Leiden university. The translation confirms that more or less (anyway in my view it does). Even after reading the 1971 translation for a third time I kept on falling from one amazement into the other. Have fun reading it, here is a link:

09 May 2019: Reason 73: In his own words; S. Goudsmit on the discovery of electron spin.

Ok, that was it for this post. Thanks for your attention (even if you are one of those sleazeballs from the Leiden university).

A classic: Imitation of the Pauli calculation given the results of the SG-experiment.

Magnetism

Often you observe people stating that the magnetic dipole moment of the electron cannot be explained by actual spinning of the electron. Because for that to happen, even if all electric charge was located on the equator of that spinning electron, it had to spin faster than the speed of light.

If memory serves, it was also Mr. Pauli (from the Pauli matrices describing electron spin stuff) that calculated this. So finally I did that calculation for myself, it takes a few minutes to collect the constants needed like the electron mass (I always forget that number). But within two or three minutes I arrived at a result of something like 15c or 15 times the speed of light.

And I started writing the text for the five pictures below and I don’t trust it and are there no errors or so? Yes there is a dumb typo on my Casio fx-82 made; it was not 15c but 15 thousand c… May be I made more dumb errors I haven’t found yet but that is all rather irrelevant because the beef of this post is not if all details of the simple calculation are correct but much more about when you can apply math in physics and when not.

For example, it is very simple math to show that the electron must spin over the speed of light and you can conclude this is not going to happen. That is more or less an allowed way of applying math in physics. Now it is not a secret that I think it is impossible that electrons are magnetic dipoles and as such I often frown over the use of the Gauss law for magnetism. If we use the variant of the Gauss law that uses a closed surface (magnetic flux through a closed surface like a spere always adds up to zero) to an electron, can we conclude the electron is a magnetic dipole because the Gauss law says so? Of course not, you absolutely need experimental evidence for such claims and only after that you can say: The Gauss law for magnetism also holds for electrons.

Not to mention you can accelerate electrons via inhomogeneous magnetic fields, you never hear about a calculation for that kind of miracle…

Ok, enough of the blah blah blah. This post is five pictures long, all of the usual size 550×775 pixels.



Ok, may be this post is just a giant mess if I read it again in a few years of time. But the huge number like 15 thousand times the speed of light can be tempered a little bit by using the so called ´Classical electron radius´ and that classical radius is far bigger compared to an electron diameter of 10^-16 meter. Here is one of those weird wiki’s:

Classical electron radius https://en.wikipedia.org/wiki/Classical_electron_radius

It looks like we are at the end of this post.

Added on 05 May 2019: A small appendix showing the difference in magnetic behavior of a single electron. I really do not know if it is possible the measure magnetic field strength of just a single electron. But at present day there are detectors that can detect just one photon, ok ok not any photon, it has to have enough energy to be detected. But anyway, if my view on electron magnetism is correct the strength should fall off in a 1/r^2 kind of law and if it is a magnetic dipole it is all very different.

Of course I cannot do such an experiment that shows how the magnetic field falls down, I do not know if such an experiment is possible. But if it is possible that experiment would likely make chopped meat of the idea the electrons are magnetic dipoles. The appendix is just one picture long, I had to enlarge it a little bit so it has size 550×850 pixels:

Again; no idea if such an experiment is possible…

And now you are really at the end of this post.

No no, you are not at the end of this post because on 30 June I also place a funny video from the Youtube channel science asylum below. I would not hold my hand in the fire for the physics in it, after all I think that it is impossible for electrons to be magnetic dipoles. I think it is magnetic charge and as such it is reasonable to talk about spin 1 particles (so basically stuff with two unpaired electrons in it). A Stern Gerlach experiment done on a spin 1 particle gives results like in the next picture and once more this validates again that electron spin is only magnetic charge…

Magnetic charge looks more reasonable to me.

Here is the video from that funny Youtube channel:

https://www.youtube.com/watch?v=sB1EPGmpzyg

Ok, that was it.