This is a lazy easy going summer post, it does not have much mathematical depth. Let’s say the depth of a bird bath. But with most posts I write you also need a lot of knowledge about what was in previous posts and for the average person coming along that is often too time consuming… So we keep it simple today; quadratic forms on 3D space.

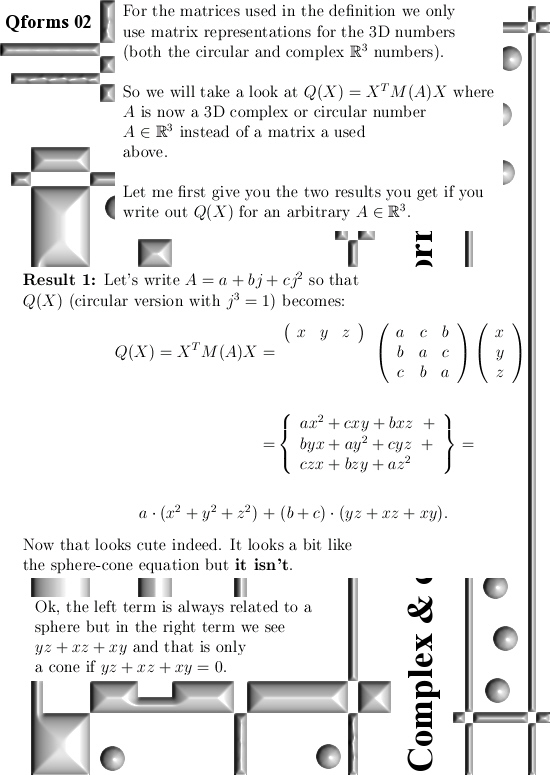
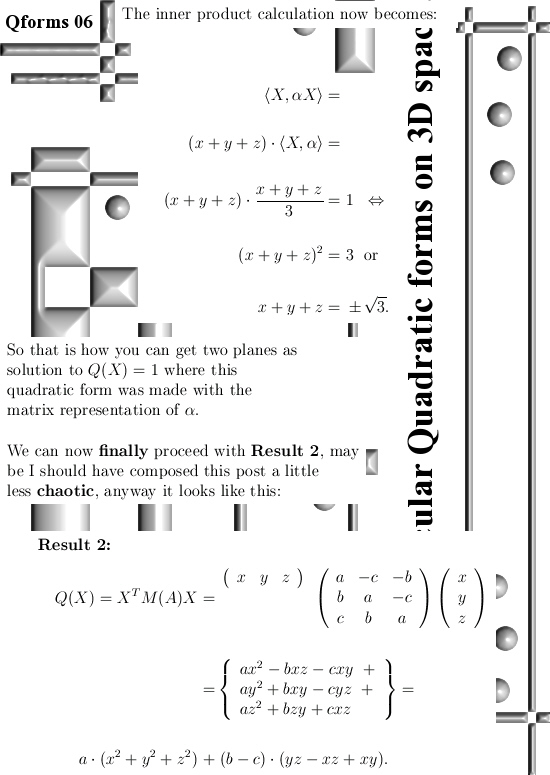
If you have had one or two courses of linear algebra you likely have encountered quadratic forms. They are often denoted as Q(X) where the X is a column matrix and the quadratic form is defined as Q(X) = X^T A X. Here X^T is the transponent of X so that would be a matrix row. As you might guess, the X column matrix contains the variables while the constant square matrix A is the source of coefficients in the quadratic form Q(X).  In most literature it is told the matrix A is symmetric, of course there is no reason at all for that; any square matrix will do. On the other hand it is easy to see or to show that if a square matrix is anti-symmetric the corresponding quadratic form will always be zero everywhere.

In this post we will take matrices that are always the matrix representation of 3D complex & circular numbers. Matrix representations are a complete category on this website so if you don’t know them you must look that up first. (Oh oh, here I go again: this was supposed to be easy but now the average reader must first try to understand matrix representations of higher dimensional multiplications…)

Compared to the previous update on the likely failure of all fusion reactors this post is far less dramatic. If in the future I am right and we will never have fusion power, that will be the difference between life and death of hundreds of millions of people in the long run… So in order to be a bit less depressing let’s lift the spirits by a lightweight new post on quadratic forms! Why not enjoy life as long as it lasts?

Ok, the actual post is seven pictures long, all in the usual size of 550×775 pixels.

I have to admit that for me the use of the number alpha was important because that is at the center of the exponential circles in the 3D complex and circular spaces. So I have a legitimate reason to post this also under the category ´exponential circle´. And from the non-bird bath deep math, that is the big math ocean that is very deep, I like to classify as much posts under that category ´exponential circles´.

Ok, let´s leave it with that and try to upload this post. Till updates my dear reader.