It is about time for a small update! Despite all that COVID-19 stuff going round, for myself after all those years I finally tried to put integration on higher dimensional number systems on a more solid footing.
All those years I just refrained from it because you cannot use my favorite Riemann sum approach because of the non-invertible numbers we have in 3D or even higher dimensions.
But now I am trying to finally make some progress and stop avoiding this subject, I find it is utterly beautiful. It has an amazing array of subtle details involved when you have some non-invertible numbers in your integration stuff.
I have no idea when I have finished this rather important detail in my cute theory of higher dimensional complex & circular numbers, so let time be time & in the meantime only post a teaser picture about that lovely integration stuff. In the first lines you see a very familiar integral, likely you have done such calculations in the complex plane. In the case of 3D circular and complex numbers you must (of course) use the multiplication on 3D space to make it all work. Basically you are evaluating (or calculating) three integrals at the same time, just like on the complex plane where you are evaluating two integrals at the same time in your calculation. If you work with a pencil & paper, make sure you have enough paper because all those 3 integrals also have 3 terms in it so your calculations can become quite long…
Here we go:

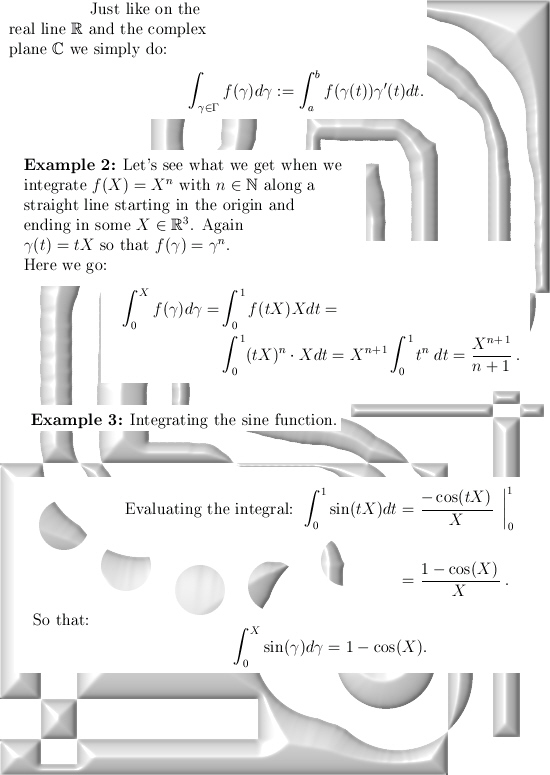
Ok, let me end this update now. Till updates and for some strange reason you must wash your hands while the proper authorities never point to 3D complex numbers… Till updates.