Monthly Archives: June 2020

Cute search engine results found & intro 4D Fourier series.

3D complex numbers, 4D complex numbers

About a week ago I started investigating how you could craft a Fourier series using the coordinate functions of the 4D exponential curve. The usual way the series of Joseph Fournier are done is with the sine and cosine that are also the building blocks of the exponential circle on the complex plane. So I needed to look up my own work on the 4D complex numbers because in the beginning of 2019 I stopped writing posts about them and after such a long time not every detail is fresh in your brain of course.
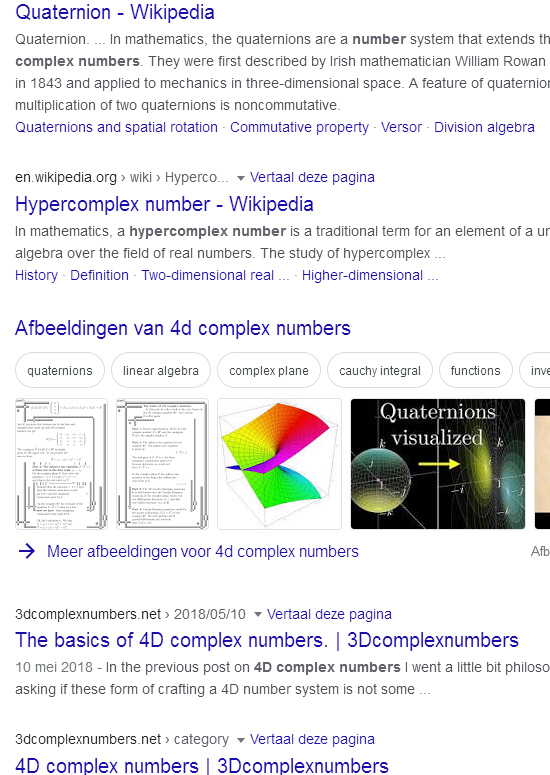
Anyway I did a Google search on 4D complex numbers and to my surprise this website popped up above where the quaternions were ranked. I was ranked number one. That was a great victory of course, it means that people are actually reading this stuff… In one of the screen shots below you see the quaternions once more topping my 4D complex numbers but from day to day it seems that Google is shuffeling the top results a bit so the search results look a bit more dynamic on a day to day basis.

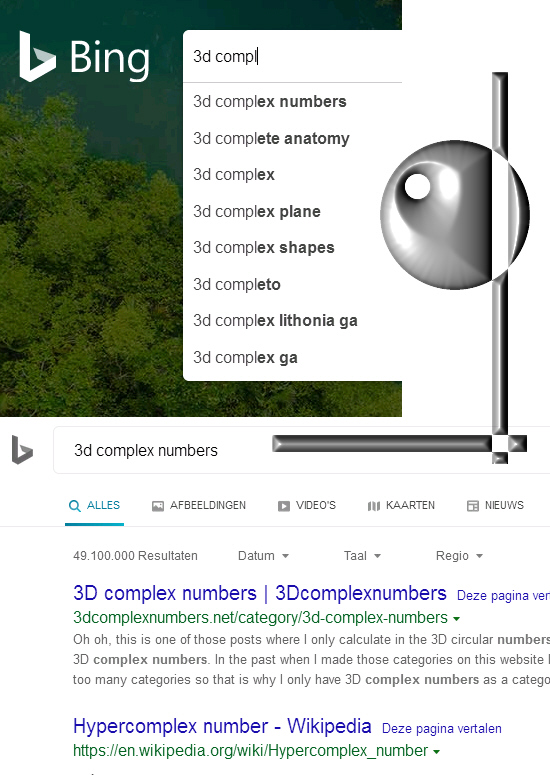
This year I didn’t look at the search engine stuff at all, we still have that corona stuff going on and beside that why look at such boring stuff if I can do math instead? But I could not resist and went to the Microsoft Bing search engine. For years they never ranked this website on page 1 if you searched for ‘3D complex numbers’. But all those years if you looked into the picture search of the Bing search engine a giant fraction of the pictures was from this website. That was very strange, how can you return so much pictures from my website while never mentioning me at any significant position in the rankings of the html files? Ok ok most people say Bing is an inferior search engine compared to the Google search engine and as such not many people use the bing thing.

So once more and for the first time in this year 2020 I searched for ‘3D complex numbers’ on the Microsoft search engine. To my surprise instead of being burried down deep on say page 10, at Microsoft they had seen the light. Here is a screen shot:

Not bad, Reinko is in pole position & where is the competition?

In the next screen shot you see the html listing of Google when you search for 4D complex numbers. Today when I made the screen shot I was not ranked at no 1 but for some strange reason that did not make me cry like a baby in distress.

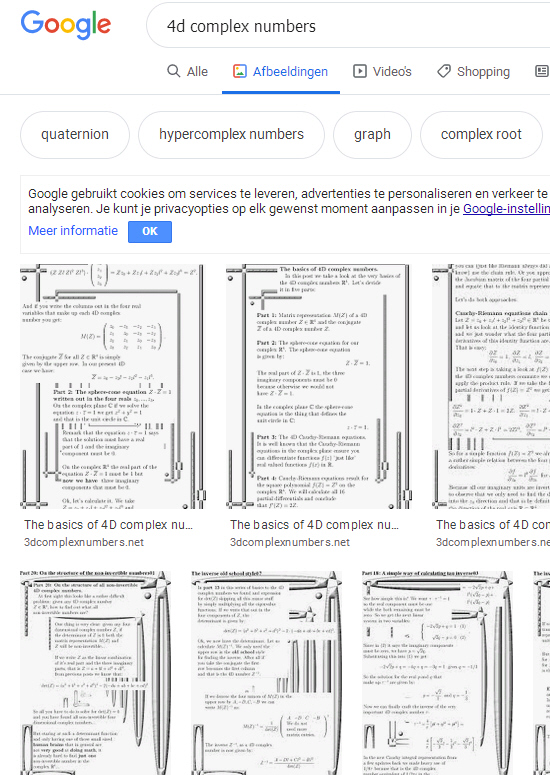
All in all there are 20 posts for 4D complex numbers.

And the last screen shot is about the Google thing for pictures when you search for four dimensional complex numbers. Luckily there is no competition but does that mean the rest of humanity is stupid as hell?

Of course not, it only means no one is interested in crafting 4D complex numbers for themselves. Professional math professors don’t want to talk about 4D complex numbers in public, so why are my internet search engine rankings that high? It might be that it is read by non math professors and that more or less explains the high rankings…

Google picture search on 4D complex numbers.

Ok, it is now 22 June and I finally wrote down what the new way of Fourier series is using the 4D exponential curve. Writing of the next post is almost finsihed and I think I am going to do it just like Joseph Fourier did. That is without any proof at al for the most important things…

Anyway, in the nexgt picture you see the Fourier series in a 4D style:

It could ber handy to look at the end of an old post from 01 Nov 2019, there I show you how you can use the modified Dirichlet kernels for finding parametrizations of the exponential circles & curves in 2, 3 and 4 dimensions. If it is possible to craft a 4D Fourier series (again this is only postulated so there is no proof at this date) you surely must try to understand the 4D modified Diriclet kernel…
Here is the link:

Two parametrizations for 3D exponential circles.

End of this post, till updates my dear reader.

A norm based on the eigenvalues of 3D complex and circular numbers.

3D complex numbers, Matrix representation

Ah, finally it is finished. This work grew longer than expected but with a bit of hindsight that is also logical: for example I spell out in detail once more how to find the eigenvalue functions for a arbitrary number X. After all that is an important detail so it is worth repeating. But I skipped the proces of diagonalization because we do not need it in this post.
Yet if you teach math and the time has come to do the complex number stuff, you could show the students how to diagonalize the complex multiplication for numbers from the complex plane. Most of the time students only diagonalize just one matrix with some numbers in it and that’s all, they never diagonalize an entire family of matrices. So that is why that would be useful, on the other hand the eigenvalues for a number z from the complex plane is z itself and it’s conjugate… And say for yourself: diagonalizing a number z so that later you must multiply the eigenvalues (also z) is very useless, as a matter of fact it is hard to find anything that is more useless… And once you have explained that diag stuff is usefull and utterly un-usefull at the same time, you can point to the live of the average math professor: also utterly useless…

Of course in higher dimensions the proces of diagonalization is very handy because it gives you for example a way of calculating the logarithm of higher dimensional numbers. And that way can be used in any dimension while all other methods for finding a logarithm get more and more difficult (as far as I know).

In this post I also worked out in detail what the eigenvalues of non-invertible numbers are; the non zero numbers with a determinant of zero have at least one eigenvalue being zero. I calcualted the eigenvalues for the numbers tau and alpha for both the complex and circular 3D multiplication.

This is post number 150 so all in all on average I write just about 30 posts a year. That is a cost of about 2€ per post… 😉 Luckily this hobby of 3D complex numbers is a rather cheap hobby while at the same time it keeps the mind sharp. A disadvantage is that if it takes me just 5 or 10 minutes to do some calculations with pencil and paper, it often takes 5 to 10 hours before it is turned into a post that is more or less readable for other people… And that is something I value highly; so often you come across sloppy explanations that are not carfully thought through. I don’t like that.

Originally I prepared 10 pictures to write the post on but I had so much text that I started expanding those pictures and in the end I made an 11-th picture to get it all on. So I just expanded those pictures to make the text fit more or less precise of most of them have weird sizes. May be it is better to just stick to the size of 550×775 pixels and just make more of them if needed and not this chaotic expansion on the fly.
Ok, here we go:

I expect that when you made it this far, you already know what the Cauchy/Schwarz inequality is. But in case you never heard of it, please try to understand that beautiful but very simple inequality. Here is a wiki: Cauchy-Schwarz Inequality. Link used: https://brilliant.org/wiki/cauchy-schwarz-inequality/

Ok, this is more or less what I had to say on the subject of crafting a norm from eigenvalues. Don´t forget in the complex plane the square of the norm is also the product of the eigenvalues of a complex number z. So for centuries the math professors are already doing this although I do not think they are aware that they use a product of eigenvalues. For them likely it is just some stuff that is ´Just like Pythagoras´.

End of this post.