I want to start with a bit of caution: In this post you can find the definition of the 4D Fourier series. It looks a lot like the definition as on the complex plane. But I still did not prove all those convergence questions. And I also do not remember very much from the time when I had that stuff as a student (that was about 30 years ago). So I don’t know if I will be able to make such proofs about convergence and what kind of functions you can use to make a Fourier series from etc etc.
Yet in this post I define a set of possible signals that I name ‘pure tones’ and these clearly have a 4D Fourier expansion because by definition they have a finite number of non-zero Fourier coefficients. Of course when you only have a finite amount of non-zero coefficients, you don’t have any kind of convergence problem. So for the time the convergence problems are avoided.
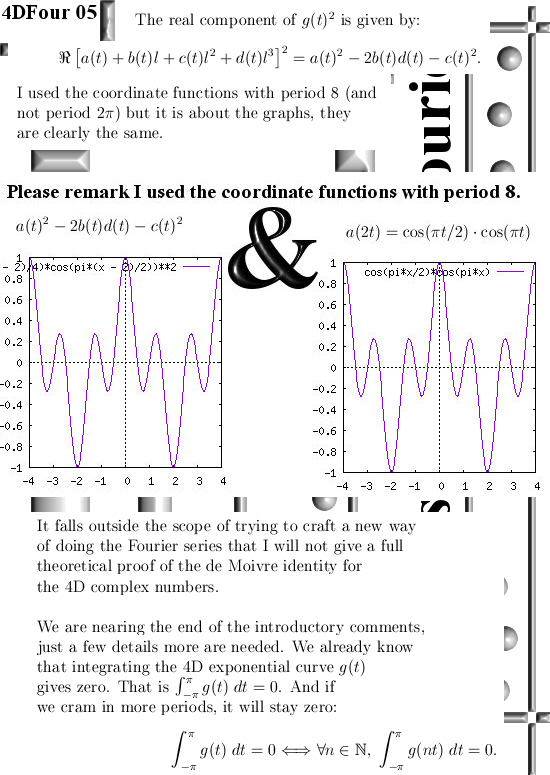
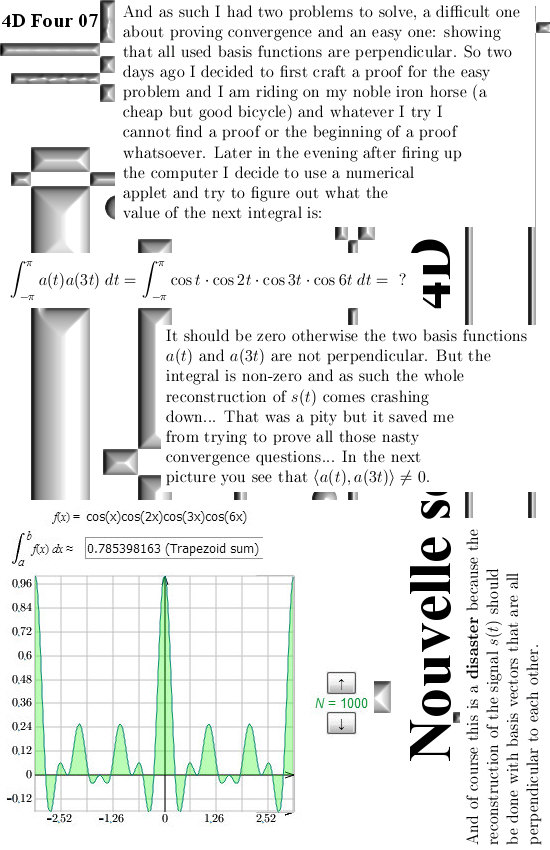
In this post, number 154 already, I hope I demenstrated enough that the basis functions used in the definition are all perpendicular to each other. After all that was a nasty hurdle we met when it was tried with just the four coordinate functions of the 4D exponential curve as our basis vectors. So we do not meet that problem again using the exponential curve as a whole. If I denote the exponential curve as f(t), the basis functions we use are basically f(nt) where n is a whole number. Just like in the previous posts I always use the notation f(t) when the period is related to the dimension and g(t) when the period is different. Here I use of course a period of two pi because that is convenient and it makes the coordinate functions more easy to write out: the first one is now cos(t)cos(2t) and the other three are just time lags of the first one. But if you want to write g(t) as an exponential, because of the period it now looks a bit more difficult compared to just e to the power tau times t.
For myself speaking I have no idea at all if crafting a Fourier series like this has any benefits of using just the definition as on the complex plane. After all I only have more or less basic knowledge about the use of Fourier series, so I just don’t know if it is ‘better’ in some regards and ‘worse’ in others.
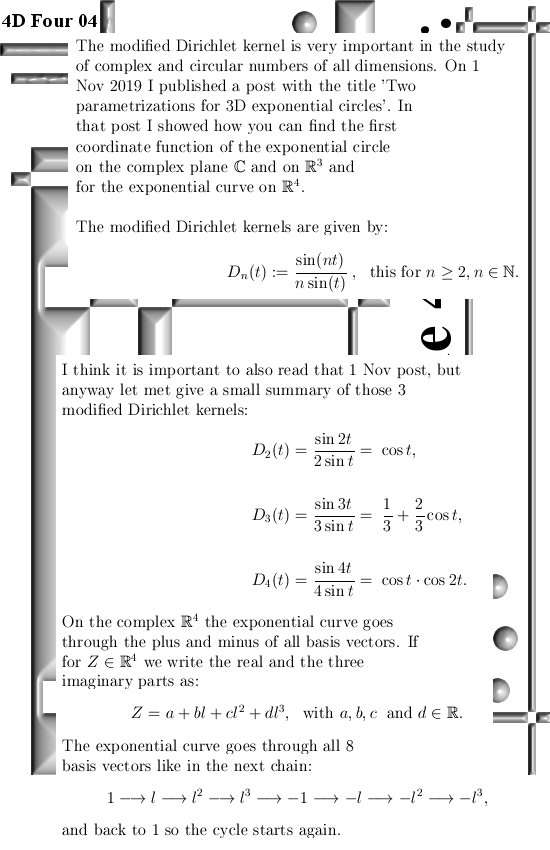
At last without doubt under my readers there will be a significant fraction that wonder if those 4D complex number system is not some silly form of just the complex plane? After all if that 4D space is based on some imaginary unit l with the property that now the fourth power l^4 = -1, how can that be different from the complex plane? The answer to that lies in the logarithm of the first imaginary unit l. If this 4D space was just some silly extension of the complex plane, this log of l should be nicely bound to i pi/4 where i is of course the imaginary unit from the complex plane. But log(l) is the famous number tau because with that you can make the exponential curve f(t) = e^(tau t). Basically the main insight is that i pi/4 makes the complex exponential go round with a period of four because i^4 = 1 and the 4D number tau makes the exponential curve go round with a period of 8 because l^8 = 1.
This post is six pictures long, all 550×775 pixels in size.





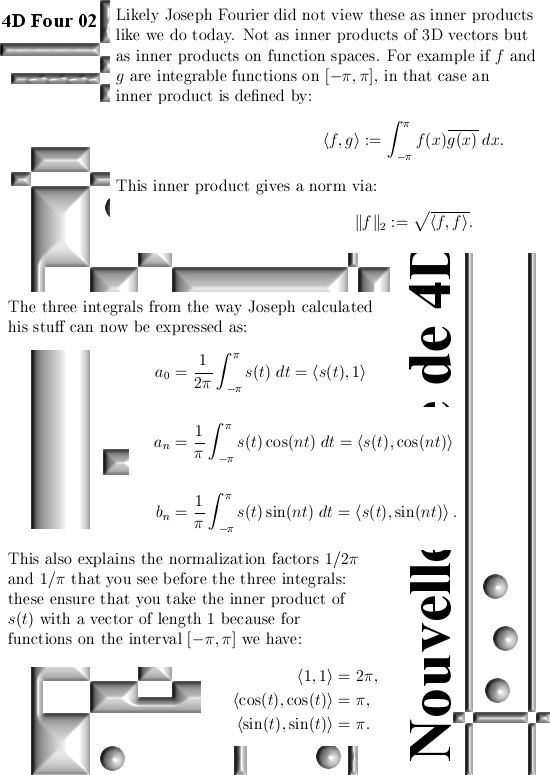
As usual I skipped a lot of stuff. For example, how did Fourier do it? After all at the time all this stuff with inner products was poorly developed or understood. That alone would be a cute post to write about. Yet the line of reasoning offered by Joseph Fourier was truly brilliant.
In case you are lazy or you want to avoid Google tracking you, here is a link to that cute symbolab stuff: symbolab.com
Link used: https://www.symbolab.com/solver/fourier-series-calculator
Ok, that is what I had to say for this tiny math update.