Warning: This post contains stuff that is not correct! Yet I decided to post it anyway so you can see that crafting math is also just keep on working until you have it right. The reason it does not work in the post below is that the basis functions I use are not all perpendicular to each other. And if you want to reconstruct a function or a signal s(t) with the basis functions as mentioned below, you will get weird overlap and the end result will not be correct.

Ok, that was a bit frustrating. But all in all I don’t have much reputation damage because more or less instantly I found another way of crafting the 4D Fourier series and that seems to work perfectly. So compared to the professional math professors who at one point in time accepted the quaternions and together with that stupid theorem of Frobenius concluded that 3D or 4D complex numbers are not possible, at least I don’t look that retarded. Sometimes I can be stupid too but at least it does not last for over one century. And may be that is also the reason that professional math professors absolutely do not want to talk about my work on 3D & higher dimensional number systems; admitting that you have been stupid for over one century is of course not an easy thing to do. And given the fact I am now unemployed for 17 or 18 years, rather likely the professional professors would rather be eating dog shit compared to speaking out my name… Once more we observe that in this world there is never a shortage of idiots.

In this post I use the coordinate functions of the exponential curve in the 4D complex numbers but I changed the period to 2 pi instead of a period of 8 that comes along with taking the log of the first imaginary unit. I also would like to mention that I use the so called modified Dirichlet kernel and because that kernel originates from Fourier analysis you must not get confused by the name ‘Dirichlet kernel’. The modified kernel is important (anyway for me) because it spits out all those coordinate functions for making exponential circles and curves in all dimensions possible. While if memory serves, the use of the Dirichlet kernel inside Fourier analysis is for using it in proofs of convergence. But may be I remember that completely wrong, after all it was about 30 years ago that I studied the Fourier stuff for the last time. The last two weeks were pleasant from the mathematical point of view, all that old Fourier stuff that somewhere still lingers around in my brain. But so much is gone, what is that Gibbs overshoot? Is that when a male math professor has his yearly orgasm? And what was the Parcival identiy? I don’t have a clue whatsoever.
This post is 7 pictures long, four are of 550×775 pixels and I had to enlarge the other three to a size of 550×850 pixels. So it is not a mess like the previous post where I just enlarged the pictures on the fly until all that text was there. Here it is:

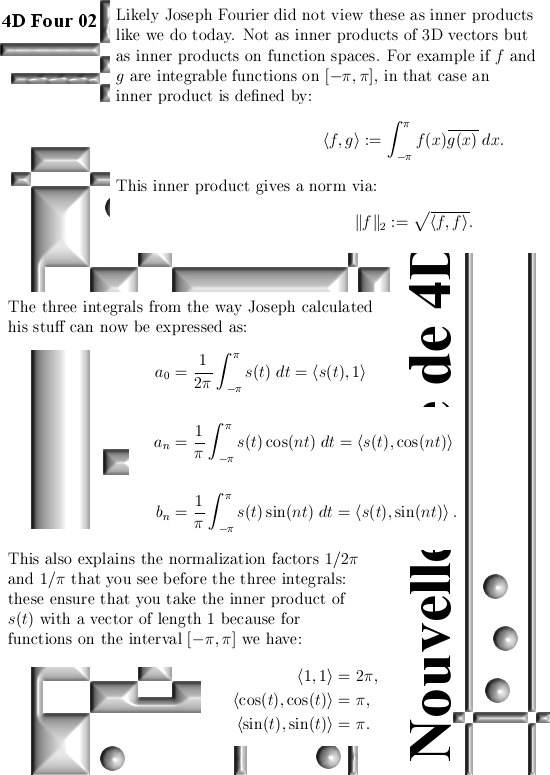
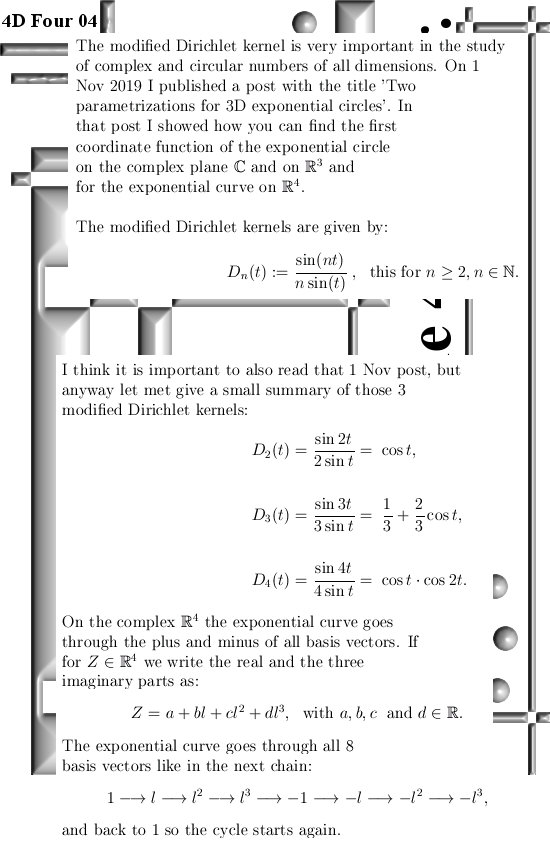
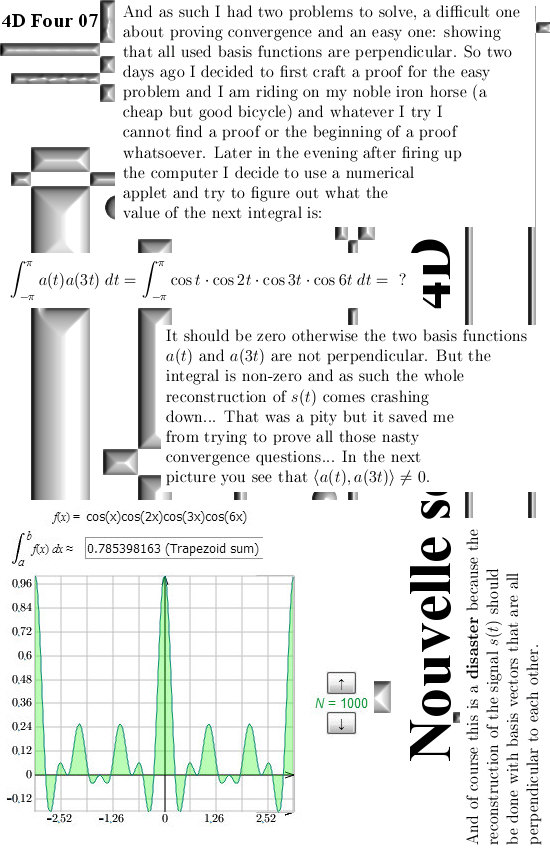
Likely all those basis functions have this problem, if you take the inner product of an arbitrary basis function against the same basis function with three times the speed, it is not zero. And as such it is not perpendicular…

For people who have never heard of inner product spaces done with functions I found a cute pdf where a lot of the basics are explained.

Inner product spaces.

I would like to be the 4D Fourier stuff done in a correct manner in the next post but sifting through what I wrote on 4D complex numbers I realized I never wrote about a de Moivre identiy for the 4D exponential curve. May be I will publish that in a separate post, may be not.
Anyway, have a good time and see you in the next update.