Two very different subjects: the earth magnetic field and the standupmath guy has a great video about the perimeter of an ellips.

Video 1) From the Youtube channel Scishow a video with the title
‘Satellite Squad Goals: The Cluster Mission to the Magnetic Field’.
For me that video contains relatively much completely new stuff, the fact that there are 4 satellites out there constantly monitoring the earth magnetic field was unknown to me.
And the presenter of the video claims that after the so called ‘magnetic reconnection’ the charged particles from the solar wind slam into the north & south pole of the earth with a staggering 10 thousand km/sec. I did not know it was that fast…
The official explanation for the acceleration of for example single electrons is that you must have an inhomogeneous magnetic field. After all these folks think that electrons have two magnetic poles and if the electron goes through a magnetic field that varies in space the two forces on the north and south pole of the electron do not cancel out and there is a net force responsible for the acceleration. There is only one problem: they simply multiply the electron magnetic moment against the gradient of the magnetic field and voila: that’s it. But if the acceleration is explained as a difference in opposing forces, should you not take into consideration the size of the electron? Yes of course, but since physics professors are so terribly smart why don’t they do this? Well if you take the size of the electron into your calculations, there is no acceleration or better it is basically zero.

Now years ago I tried to estimate how stong a magnetic field had to be to accelerate one of those dipole electrons with a acceleration of only 1 meter per second squared. If memory serves I used an ‘electron size’ of 10 to the power -15 meter (in reality it is even much smaller) and again if memory serves you needed magnetic fields with a gradient of over 100 thousand Tesla per meter.
And if you think about that estimation it makes a lot of sense: electrons are very small and as such have an extreme density given their size and mass. Say it is in the order of the density of a neutron star. And if you try something with the density of a neutron star to accelerate with the difference of a magnetic field, likely you won’t go far…

Ok, suppose for the moment that the electrons are the long sought magnetic monopoles. So they are not magnetic dipoles but the electrons themselves are magnetic monopoles just like they are electric monopoles.
Now look at the picture below: it is about when the magnetic reconnetion just closed. Just before the closing along the magnetic field lines emergin from the earth north & south pole, the particles were expelled because they carry the wrong magnetic charge. But when reconnection takes place, the particles that were expelled by say the earth south pole find themselves back on a trajectory going to the earth north pole. And as such they will get accelerated into that direction.

Yet a couple of years ago when I published those estimations that show you need crazy gradients for all that shit to be true, of course nobody reacted. All those university professors in physics, when you tell them that extra ordinary claims like the electron being a magnetic dipole also needs extra ordinary proof, all of a sudden they are deaf deaf deaf.
These people they don’t have any experimental proof that the electron is a magnetic dipole. And worst of all: They don’t even think about it…
Finally, here is the SciShow video:

Video 2) From the Standupmath guy a video about the perimeter of an ellipse. Weirdly enough it is not possible to find a more or less simple expression for the perimeter of an ellipse. Of course a long long time ago I tried to find an expression myself but using the standard stuff like arc length brings very fast a lot of headache. With the present day of math tools it is completely not possible to derive a good expression for the perimeter of an ellipse.
What I did not know is that there is a world of approximation stuff out there for estimation such ellipse perimeters. And of course in itself this has it’s own logic: after all an ellipse is more or less completely defined by saying what it’s two half axes a and b are. You can always fix one of those axis to 1 say b = 1 and study the perimeter problem as a function of the variable a. You do some curve estimation, you drink a few pints of beer and later when you are sober again you drink some green tea.
And you conclude some curve estimation is relatively good but that all in all the ellipse perimeter problem is just too large for our human brains that in general are not good at doing math.
There is only one exeception; Ramanujan.
In the next picture you see one of those Ramanujan approximations and once more you see how the human mind should work if we were living in a better world:

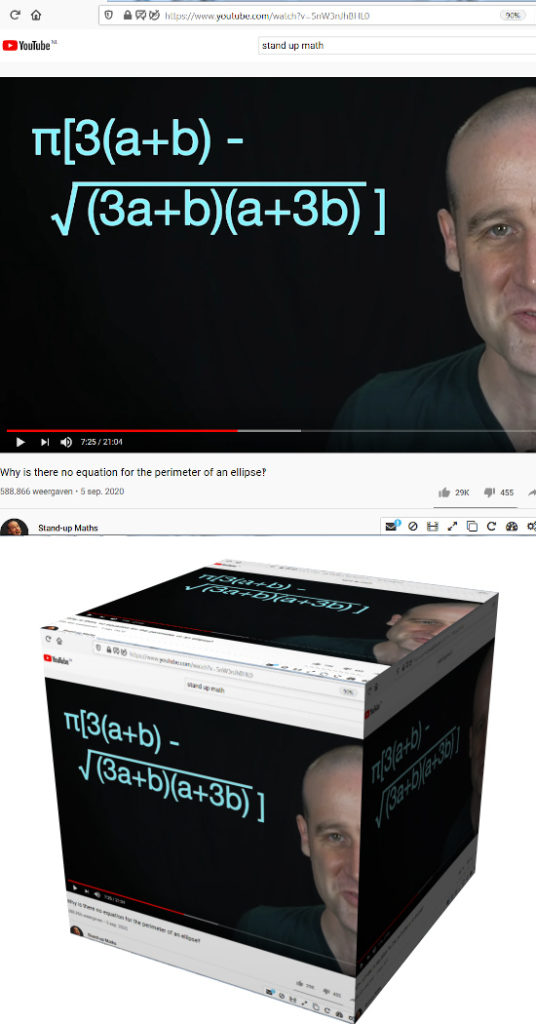
The video is here, 21 minutes long but worth the time:

Ok, that was it for this post. Think well, live healty and try to make some bio fuel from the basic ingredient known as ‘math professor’.
In that case we will find ourselves back in a better world, or not?